Salut les matheux ,

Je cherche à définir un modèle mathématique pour un jeu vidéo.
Pck sans modèle, pas de jeu ^^.
J'ai fait un petit résumé qui à défaut d'être moins précis donne la grande majorité des données.

En résumé :
Je cherche la méthode de calcul pour générer la trajectoire idéale pour un mobile dans un environnement 2D avec différentes contraintes (angle de rotation maximum, poussée minimum et maximum, points de passage, friction qui ralentit le mobile « naturellement » toutes les unités de temps), et quelques tolérances (notamment il n'est pas obligatoire de passer exactement sur le point de passage qui est en réalité un cercle).

Du coups je cherche à modéliser la courbe idéale passant par 3 points (le départ, un point de passage, le point de passage suivant).

Après quelques recherches il semblerait que 3 solutions sortent du lot (mais peut-être une autre solution pourrait exister) :
- Courbe de Bézier
- Courbe clothoïde
- Exploiter des calculs d'asservissement.
- Autre ?

Mais en finale je fais tout ça dans mon coin. Et même si j'ai de bonnes notions de math, ça reste des notions. Et j'avoue qu'étudier ces 3 sujets et trop de travail pour moi.

En détail :
Bon je risque de me répéter par rapport à ce que j'écris dans le résumé (en mm temps c'est un peu l'idée d'un résumé xD).

Je cherche la méthode de calcul pour générer la trajectoire idéale pour un mobile dans un environnement 2D avec différentes contraintes, et quelques tolérances.
Liste des contraintes et tolérances :
- Angle de rotation maximum (de l'ordre de 15° mais pourrait devenir variable, quand le mobile tir, active un booste de poussée, ou autres, donc ne pas le considérer comme une constante dans les calculs). Sachant que j'ai bien sur à ma disposition l'angle de départ.
- Poussée minimum et maximum (pour le moment je ne considère pas le freinage et je cherche simplement un % de la poussée maximum, je ne sais même pas si j'ajouterais la notion de freinage par la suite)
- Des points de passage qui sont des cercles avec un centre défini en x/y et un rayon (pour le moment je pensais « viser » le centre, surtout si je vais sur des calculs d'asservissement où dans ce cas l'instabilité au passage du point devra être maximisée sur ce rayon, mais j'avoue que ces calculs me font un peu peur et risquent de me demander un gros investissement de temps pour les comprendre).
- Une friction qui ralentit le mobile « naturellement » toutes les unités de temps. Le facteur sera de l'ordre de 0,8, et donc la vitesse à t+1 sera calculé comme ça :
-> x = (vx + « Poussée max sur x » * % de poussée) * « facteur friction » ;
Avec :
- x la nouvelle vitesse en x
- vx la vitesse actuelle en x
- « poussée max sur x » fonction de l'angle courant de véhicule et d'une « constante » (pourrait devenir variable)
- « facteur friction » : pareil pourrait devenir variable (pourrait devenir variable)

Pour résoudre ce « système » et après quelques recherches, il semblerait que 3 solutions (plus ou moins complexes) pourraient donner des résultats :
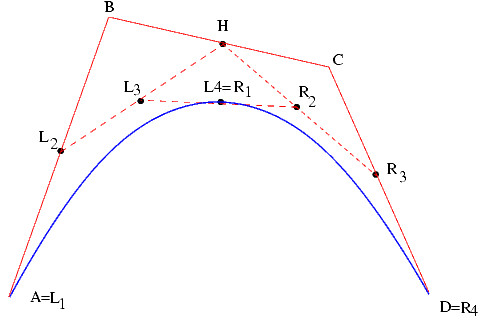
- Des courbes de Bézier :
cf. 1ere image
Avec un calcul intelligent des segments AB et CD sachant de A est mon point d'origine, R1 et prochain check-point, et D le check-point « final » je pense qu'il devrait y avoir moyen de faire qq-chose.

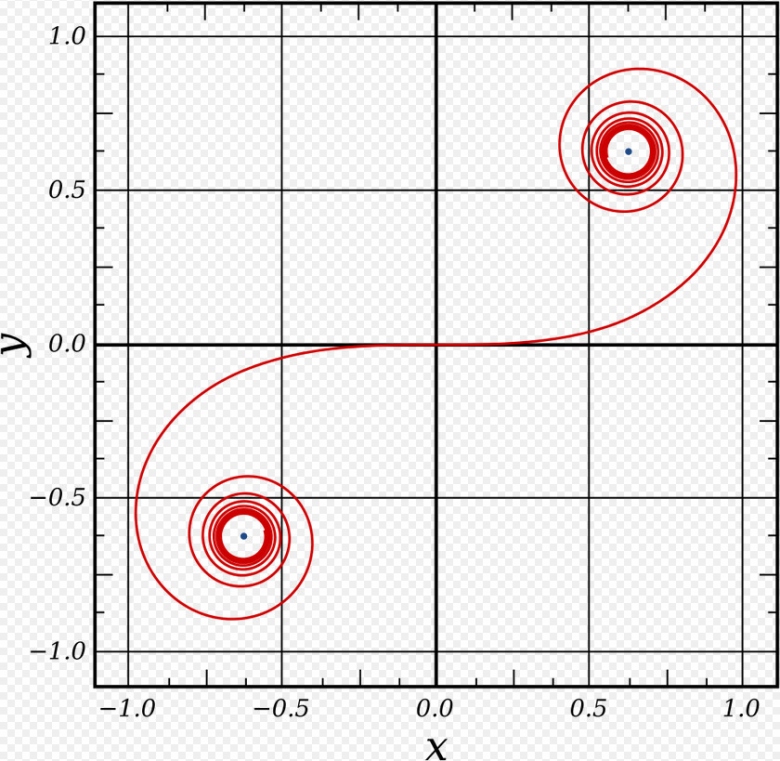
- Des courbes clothoïdes
J'avoue que là je nage déjà en eaux troubles. Mais si j'en crois mes recherches c'est ce qui est utilisé pour calculer la courbure idéale des autoroutes, ce n'est probablement pas pour rien.
cf. 2eme image
Bah je vois pas comment exploiter ça pour le moment.

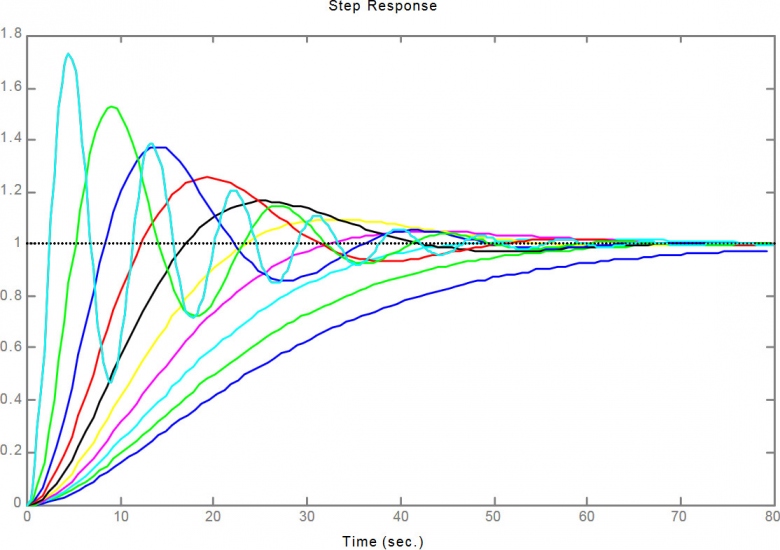
- Extrapolation de calcul d'asservissement :
Alors là, je ne nage plus en eaux troubles, mais je suis carrément noyé. Par contre cela me semble aussi la solution la plus prometteuse.
cf. 3eme image
Après quelques coups d'œil aux formules, je me suis évanouie (deux fois), puis me suis revue à l'école entrain d'écarquiller les yeux devant ces calculs appliqués à de l'asservissement thermique. Et je me suis décidé à demander de l'aide.

- Il existe peut-être une autre solution encore plus efficaces que je n'ai pas identifié et là je me renseignerai sur vos propositions.

En tout cas, merci de m'avoir lu.
Je pourrais être parfois un peu long à répondre, je fait ça sur mon temps libre