Inscription / Connexion Nouveau Sujet
Deux cercles sécants et une tangente commune ...
Voici un petit exo qui me turlupine depuis que je suis tombé dessus. J'ai beau le retourner dans tous les sens, je ne fais que rester spectateur de l'observation sans parvenir à rien démontrer.
Le voici :
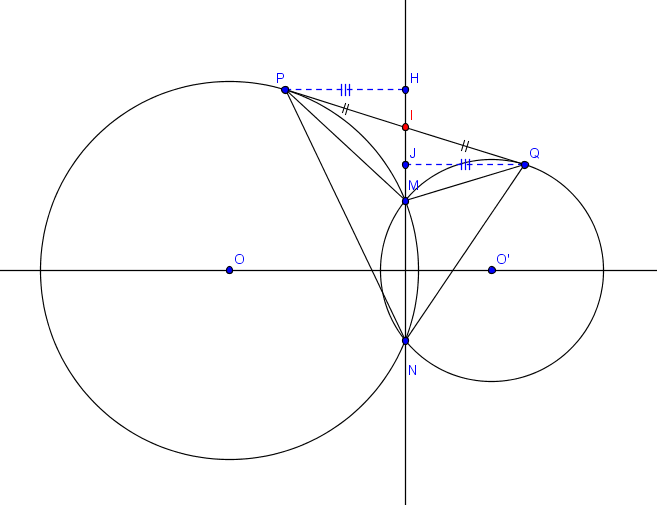
"Dans le plan, on se donne deux cercles sécants et on désigne par M et N les points d'intersection de ces deux cercles.Une tangente commune à ces deux cercles les touche respectivement en P et Q. Montrer que les triangles MNP et MNQ ont même aire."
L'énoncé est simple et bref comme vous pouvez le voir, mais justement c'est là que se joue tout le problème j'ai l'impression ...
En espérant que vous ayez plus d'intuition,
je suis preneur de la moindre piste 
Je dirais que c'est parce que la droite MN coupe le segment PQ en son milieu I.
La raison en est que cette droite est l'axe radical des deux cercles, de sorte que ce point I a même puissance par rapport à l'un et l'autre cercle. Par suite, IP = IQ.
J'en étais pour le moment arrivé justement à cette conclusion, c'est-à-dire que la droite (MN) coupe [PQ] en son milieu I. Toutefois, je ne parvenais pas à le démontrer mais seulement à en faire la conjecture. Pourrais-tu préciser quelque peu ? Qu'entends-tu par axe radical je suis en Terminale et c'est la première fois que j'entends ça ?
Merci d'avance
Merci pour ces précisions sephdar, même si j'avoue que je ne comprends pas tout ce qui est dit à propos de ce fameux axe radical.
Simplement pour me faire une idée, si ce n'est pas au programme de lycée, saurais-tu quel est le niveau requis pour normalement pouvoir résoudre cet exercice ?
De plus, pourriez-vous m'expliquez peu ou prou ce à quoi correspond la puissance d'un point puisque ceci apparaît comme la clé pour comprendre le concept d'axe radical ? (En fait, j'ai trouvé cet exo en cherchant des exercices d'un niveau un peu plus relevé en vue du Concours Général de Maths d'où ma curiosité pour ces notions qui dépassent un peu le programme officiel) 
Bonjour,
Un dessin:
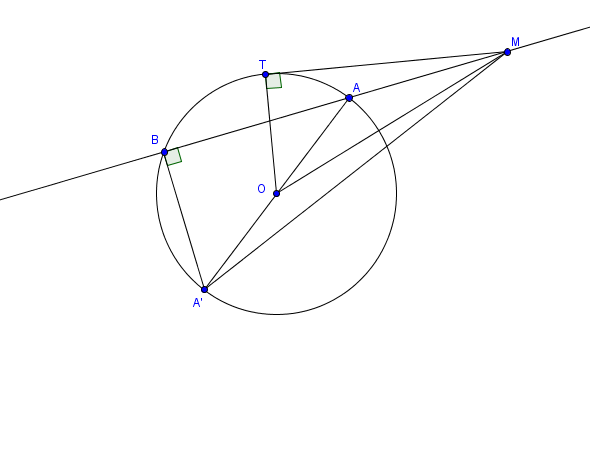
Un cercle de centre et de rayon
est donné.
Par un point (ici extérieur au cercle), passe une droite sécante avec ce cercle en
et
On s' intéresse au produit scalaire ;
Soit le point diamétralement opposé à
:
Autrement dit, ce produit scalaire est indépendant de la position de la sécante passant par
Par définition, on l' appelle "Puissance du point par rapport au cercle
" noté
On peut faire une démonstration analogue si est intérieur au cercle.
Un cas particulier (dans le cas où est extérieur au cercle): la droite est tangente au cercle en
; on a:

Ok merci pour ton aide, je suis parvenu à la solution grâce à la notion de puissance de I par rapport aux deux cercles ce qui permet d'aboutir à IP²=IQ² d'où I milieu de [PQ] et par voie de conséquence à la solution. 
Bonsoir
En version classique.
1) Si d'un point, on mène une sécante à un cercle, le produit des distances du point aux intersections de la sécante et du cercle est le même, quelle que soit la sécante. Ce produit est appelé puissance d'un point par rapport à un cercle.
Dans le cas où un point P est extérieur au cercle, si deux sécantes partant de P rencontre le cercle l'une en A puis en B, l'autre en Cpuis en D, les triangles PBC et PDA sont semblables car ils ont en commun l'angle P et leurs angles inscrits B et D sont égaux comme interceptant le même arc. PA/PC = PD/PB et donc PA*PB = PC*PD.
Ce produit constant est appelé puissance d'un point par rapport à un cercle.
2) La tangente mené d'un point à un cercle a pour carré le produit des distances de ce point aux intersections avec le cercle de toute sécante menée du point au cercle.
Soient P le point, O le centre du cercle, T le point de tangente et A et B les intersections de [AO) et du cercle. Dans le triangle rectangle PTO, PT² = PO²-Ot² = (PO-OT)*(PO+OT) = (PO-OA)*(PO++OB) = PA*PB. Or, [PO) n'est qu'une sécante particulière menée de P au cercle.
(Cette propriété offre une méthode pour construire la longueur moyenne proportionnelle à deux longueurs données.)
En appliquant cela au problème : IP² = IM*IN et IQ³ = IM*IN, d'où IP = IQ.
Les triangles NIP et NIQ ont la même aire car ils ont une hauteur commune et des bases égales; de même les triangles MIP et MIQ; par différence, les triangles MNP et MNQ ont la même aire.