Bonjour, j'ai un devoir de math à faire. Je l'ai fait mes souhaiterai savoir s'il comporte des erreurs . Le graphique est joint dans le lien.Merci

Exercice :

Le plan est rapporté à un repère orthonormal. Soit f la fonction définie sur l'intervalle  [-1;2] dont on donne la courbe représentative C sur la figure ci-dessous. La droite (EF) est la tangente à la courbe C au point d'abscisse 0.

1) Utiliser ce graphique et les informations de l'énoncé pour répondre aux questions suivantes :

a) Déterminer : f(1) et f(2)
J'ai mis f(1) = -2 et f(2) = 2

b) Déterminer le coefficient directeur de la droite ( EF) . En déduire f'(0).
J'ai mis CD = -3 ( J'ai -3-3 / 2 = -3 ) et f'(0) = - 2

c) Donner le nombre de solutions sur l'intervalle [-1;2] des équations suivantes :
f(x)= 3, f(x)=1 et f(x) = -2
J'ai mis f(x)= 3 à aucune solution
f(x)=1 à deux solutions 0.35 et 1.80 environ
f(x)=-2 à une seule solution qui est 1

d) Résoudre sur l'intervalle [-1;2] l'équation f(x) = 0. Donner une valeur approchée à 0,1 près du plus grand de ces deux nombres.
J'ai mis f(x)=0 à deux solutions 0 et 1,75.

e) Résoudre sur l'intervalle [-1;2] :
f(x)> 0 et f'(x)0

J'ai mis pour f(x)>0 ]-1;0[U]1,75;2[
pour le suivant j'ai faux mais j'ai mis S= [0;1,75]

f) Dresser le tableau de variation de f sur [-1;2]
Je ne sais pas faire les tableaux sur ce forum mais j'ai mis en face de x = -1; 1 et 2 et que la flèche baisser de -1 à 1 ( avec comme image de -1 = 2 et comme image de 1 = -2) et qu'elle augmenter de 1 à 2 ( avec comme image de 2 = 2 ).

2) On admet que pour tout nombre réel x de [-1;2], f(x) = a+bx, où a et b sont des constantes.
A l'aide de résultats obtenus à la question 1a); déterminer les coefficients a et b.

J'ai mis f(1) = -2 donc a + B = -2 et f(2)= 2 donc 8a+2b = 2
Ce qui donne un système qui me donne comme résultats a = 1 et b = -3

Merci pour votre aide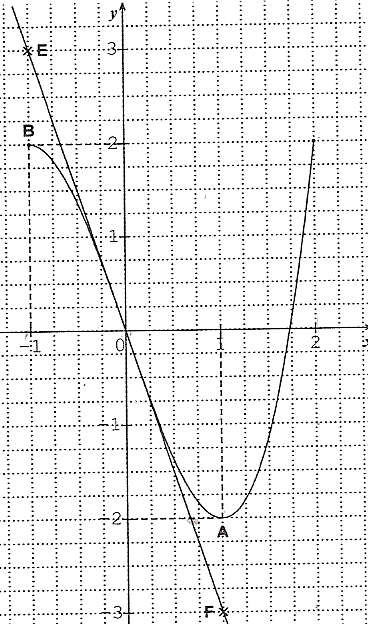



_{* Océane > image placée sur le serveur de l', merci d'en faire autant la prochaine fois Tweety0242 *}