Inscription / Connexion Nouveau Sujet
Différence entre Fonctionnelle et Application
Bonjour j'aimerai comprendre clairement la différence entre fonctionnelle et application.
Une application est la donné de 3 choses :
- Un ensemble de départ (le domaine de définition)
- Un ensemble d'arrivé
- Une recette : qui associe à tout élément de l'ensemble de départ un unique élément de l'ensemble d'arrivé
Une fonctionnelle est (d'après ce que j'ai compris) diffère d'une application dans le sens ou les éléments de l'ensemble de départ peuvent être liés à plusieurs images.
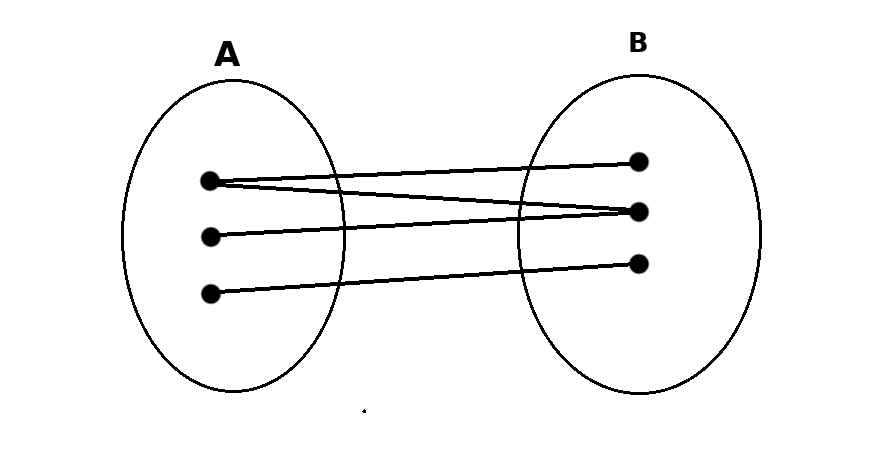
Le diagramme sagittal que j'ai mis en pièce jointe est bien une fonctionnelle n'est-ce pas ?
Bonsoir
à un élément de l'ensemble de départ on peut associer au plus un élément de l'ensemble d'arrivée
ainsi vous n'avez pas donné le graphe d'une fonction car la premier élément de A aurait deux images
de chaque élément de l'ensemble de départ ne peut partir qu'au plus une flèche
D'accord autant pour moi, donc une fonctionnelle en gros on peut dire que c'est comme une injection mais pour l'ensemble de départ n'est-ce pas ?
ex (pièce jointe) ça c'est fonctionnelle ?
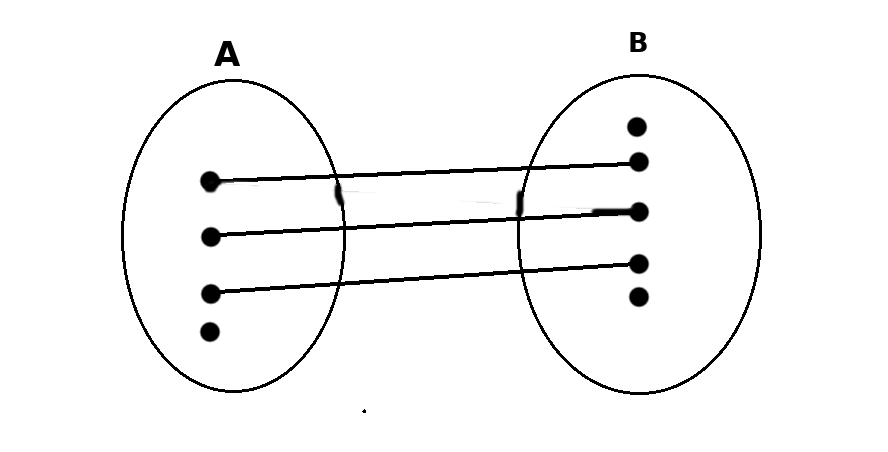
oui mais vous pouvez avoir des flèches qui arrivent au même point
prenez par exemple sur toutes les flèches arrivent sur le réel
de chaque élément de l'ensemble de départ il ne part qu'au plus une flèche pour une fonction
une application est injective si deux images sont égales c'est qu'elles proviennent du même élément
salut
à la fonction définie sur
correspond l'application
définie sur
dans le premier cas tout élément de R+ possède une image
dans le deuxième cas tout élément de R possède au plus une image
...
salut,
quand on ecrit "soit f la fonction definie sur A telle que f(x)=..."
cela signifie que l'ensemble de definition de f est A.
d'accord merci bcp pour vos explications donc toute application est fonctionnelle mais l'inverse est faux
salut
à la fonction
dans le premier cas tout élément de R+ possède une image
dans le deuxième cas tout élément de R possède au plus une image
...
D'accord donc toute application est une fonctionnelle mais pas l'inverse n'est pas toujours vrai ?
oui en général on ne s'intéresse qu'aux applications l'ensemble sur lequel la fonction n'est pas définie n'a guère d'intérêt
Prenons par exemple les diagrammes sagittaux présents ci-dessous, sommes nous d'accord pour dire que :
a) est une relation binaire fonctionnelle
b) est 
c) est une application surjective
d) est une application bijective

(a) n'est pas une relation fonctionnelle a et d ont deux images
(b) est une application tout élément de E a une unique image
(c) est une application surjective
(d) est une application injective et surjective c'est une bijection
est l'application (b) est quoi ? Une application peut être ni injective ni bijective ni surjective ?
oui toutes les applications ne sont pas injectives ou surjectives
c'est une application
c'est une surjection
c'est une bijection
ah oui effectivement merci beaucoup!
et par curiosité à quoi correspond le (a) ? Est-ce que ça a un nom le fait qu'un élément de l'ensemble de départ admette plusieurs images?
une relation est la donnée de 3 ensembles E, l'ensemble de départ, F, l'ensemble d'arrivée et le graphe G partie de
est en relation avec
si et seulement si
et