Bonsoir,

Je pense qu'avec une longueur de 14,39 m cela devrait passer.

Je trouve une longueur maximale de 14,3591m.
Avec deux chiffres celà donne L=14,35 mètres

bonjour Monrow
la longueur maximale est
14,35 m arrondi au centimètre inférieur (ce qui s'indique vu la nature du problème)
14,36 m arrondi au centimètre le plus proche
plus exact : 14,359165 m

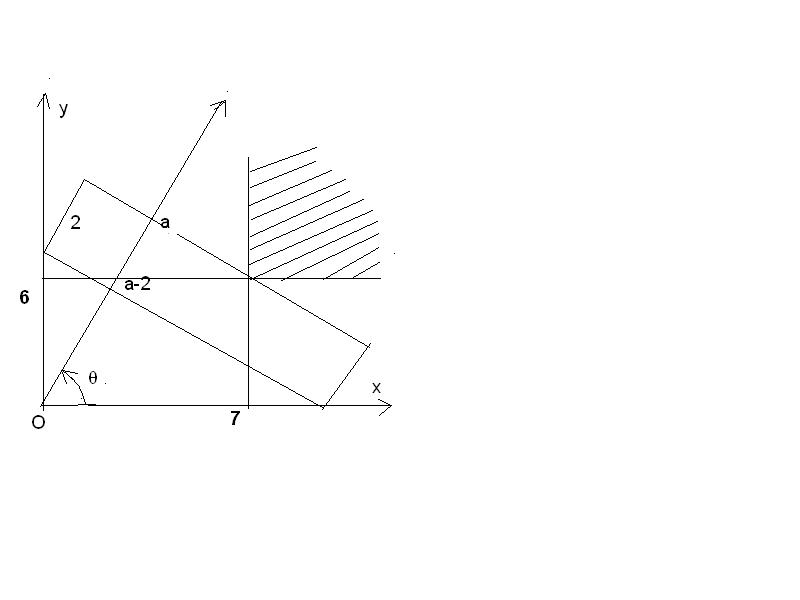
soit a l'angle que forme à un moment donné le côté droit du camion avec le côté haut du square
à l'arrière, le camion peut se permettre une longueur de 6/sin(a) - 2/tan(a)
à l'avant, le camion peut se permettre une longueur de 7/cos(a) - 2tan(a)
dans l'intervalle ]0;pi/2[ le minimum de 6/sin(a) - 2/tan(a) + 7/cos(a) - 2tan(a) est environ 14,359165 (pour a vers 0,7492 radian)

Bonsoir Monrow

Très dur cette énigme!!

En espérant que je me suis pas trompé dans mes calculs, ni dans mon petit programme je réponds Lmax = 14.36 m.

merci bien pour l'énigme .

Jolie énigme! Merci Monrow.

Comme le camion s'est déjà engagé, dire qu'il peut continuer son trajet équivaut à dire qu'il peut faire la manoeuvre complète.

En prenant un repère convenable, on a le dessin ci-dessous.
Le flan du camion qui frôle le mur du jardin a pour équation .
Il passe par l'angle du jardin donc .
La longueur du camion est
Pour fixé, cette longueur est la longueur maximale du camion pouvant se positionner comme sur le dessin.
Le minimum sur de cette fonction de nous donnera donc la longueur maximum à donner au camion si l'on veut qu'il fasse la manoeuvre complète.
L'étude des variations de la fonction à l'aide de la dérivée n'est pas très engageante. Je m'en tiens à une étude graphique à l'aide de Maple.
En faisant varier de 0.1 à 1.5, on voit bien que la fonction passe par un minimum.
On restreint de plus en plus l'intervalle de variations de jusqu'à voir que  le minimum est pour entre 0,8216 et 0,8217. Sur cet intervalle, là fonction  reste égale à 14,3592..
J'arrondis au cm inférieur (sage précaution!)

La longueur maximale du camion est de 14,35 m.

A bientôt!

la longueur maximal L est :L=((7*7)+(6*6)) -0.01
alors L=9.20m

Bonjour,

La longeur maximale du camion est L 14,359 m.

L'arrondi à la valeur la plus proche (14,36 m) ne permet pas au camion de passer le virage.

Je propose donc la valeur arrondie par défaut: L = 14,35 m.

A+

Bonjour monrow

Par une méthode numérique, je trouve que la longueur maximale du camion est 14,359165...

Comme il faut 2 chiffres après la virgule, j'arrondis par défaut à 14,35 m.

(Car avec la valeur la plus proche soit 14,36 m, ça frotte !)

Cordialement
Frenicle

Bonsoir,

J'ai un peu la flemme de détailler mes calculs et de faire un schéma pour aller avec
mais je trouve une longueur maximale de 14,36 m pour le camion.

longueur maximale
((85 -2)*(7/6+6/7)14,6109...
L14,61 m

Prenant l'origine au coin des deux rues,
soient (a, b) les coordonnées du coin C du jardin avec a=7, b=6, et d=2 la largeur du camion. Le coté extérieur du rectangle représentant le camion sera un segment de longueur l dont les extrémités sont sur les axes, et au plus près, ce segment sera à une distance d  de C ; l'équation de la droite qui le porte sera donc de la forme :
(x-a)cost + (y-b)sint+d=0 (en désignant par t l'angle du vecteur normal). Les extrémités du segment sont donc (acost+bsint-d)/cost, 0) et (0, acost+bsint-d)/sint), sa longueur vaut l=(acost+bsint-d)(1/cos2t+1/sin2t)1/2=(acost+bsint-d)/(sintcost), dont la dérivée par rapport à t s'annule si a(cost)^3-b(sint)^3+d((cost)^2-(sint^2)=0, qu'il faut résoudre par des moyens graphiques ou numériques.
Tous calculs faits, avec les valeurs numériques du problème, on trouve une valeur maximale de l=14,366..m, arrondi à 14,37m
A noter que l'enveloppe du coté extérieur du camion, est une branche d'astroïde, ou hypocycloïde à 4 points de rebroussement (H4), et celle du coté intérieur une hypotrochoïde parallèle à l'astroïde.

L = 32^(1/2)  +   45^(1/2) =  12,36 mètres (sans arrondir)
                           =  12,37 mètres (en arrondissant)

A+
Torio

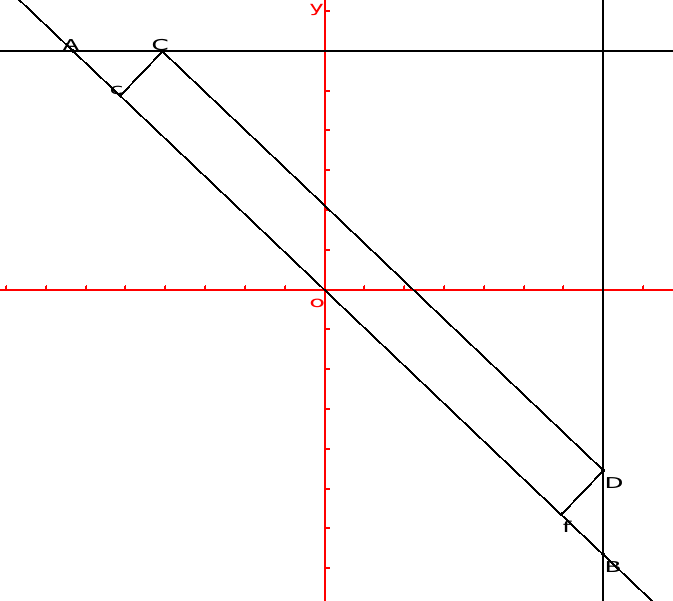
Voila ma solution :
d'abords cherchons la longueur maximale d'un segment qui pourrait passer le carrefour :
soit a l'abcisse du point A
L'équation de la droite Ao s'écrit y=(6/a)*x
Elle coupe Y pour x=7, Yy (ordonnée de Y) = (6/a)*7
Donc la longueur du segment AB en fonction de a s'écrit :
f(a)=

soit f(a)=
On cherche le minimum de cette fonction, donc quand sa dérivée s'annule :
f'(a)=
Donc il faut que a^3+252=0 soit a= ou a=-6.31636.
Maintenant revenons au camion, de largeur 2m :
il s'agit donc de trouver la longueur minimale du segment CD, on connais la longueur minimale de (AB), l'équation de la droite (AB), on sait que (cC) perpendiculaire à (AB) et cC=2,(fD) perpendiculaire à (AB) et fD=2.
L'équation de la droite (AB) est y=(6/a)*x donc l'équation de la droite (cC) est y=-a/6*x+b.
Trouvons les coordonnées du point c :
On considère la fonction y=-a/6*x et le point A(xa,xb).
Pour que OA=2 il faut que =2
Soit xa=.
Et ya=.
Pour en revenir à la figure et le camion, cela signifie que le point c a pour ordonnée  yc=6-ya et il est sur la droite (AB). On connait donc les coordonnées du point
c = ( ;   )
Trouvons les coordonnées du point f :
Toujours en utilisant le principe du point A, on utilise xa :
On a xf=7-xa. f est sur AB donc ...
f a pour coordonnées (   ;    )

Et maintenant, le calcul final !
Longueur du segment
cf=

En simplifiant, cf=

On remplace a par

Valeur approchée de cf=14.36133876112909
Dans le problème, cf correspond à la longueur L cherchée, arrondie, L = 14.36 m

BONJOUR,
La longeur maximale du camion est:6,50 métre.

Bonjour.

Je la connais celle-là...

La longueur du camion doit être au maximum 14,36 m.

Merci pour l'énigme.

Salut à tous, voici ma réponse :

L14.39 m

Voilà

matovitch

Bonjour

On conçoit que le point difficile, pour le camion, sera quand il tournera en frôlant les contacts avec :
- le point O, au coin des deux rues,
- le point C sur le bord haut de la rue de Mongolie,
- le point D sur le bord droit de la rue de Chine.



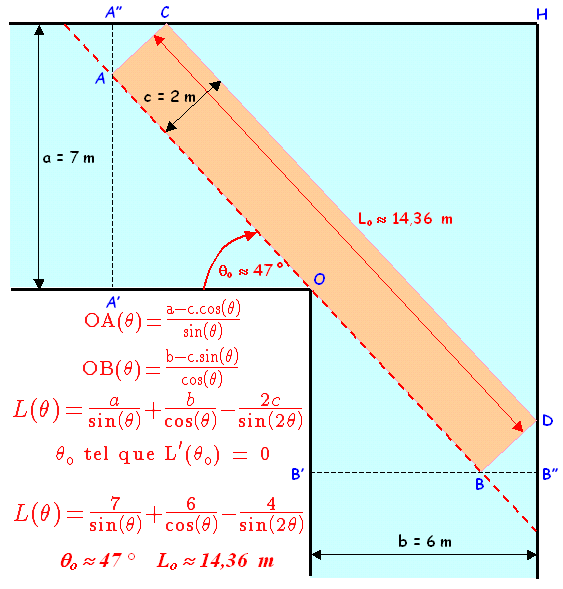
Exprimons les distances OA et OB en fonction de theta = t, l'angle de rotation autour de O :
- A est tel que le point C soit sur l'horizontale de H
- B est tel que le point D soit sur la verticale de H

Détaillons pour OA :
Dans le triangle OAA' on a AA' = OA.sin(t)
Dans le triangle CAA"  on a AA" = AC.cos(t) = c.cos(t)
Ainsi, A'A" = OA.sin(t)+c.cos(t); or A'A" = a
OA(t) = ( a - c.cos(t) )/sin(t)

De la même façon, avec les triangles OBB' et DBB", on obtient :
OB(t) = ( b - c.sin(t) )/cos(t)

Comme L(t) = OA(t) + OB(t) = ( a - c.cos(t) )/sin(t) + ( b - c.sin(t) )/cos(t)

L(t) = a/sin(t) + b/cos(t) - 2c/sin(2t)

En étudiant L(t), on montre que L passe par un minimum tel que L'(t) s'annule en changeant de signe.

Avec a=7m, b=6m et c=2m, on trouve les valeurs approchées t = 47° et L = 14,36 m.



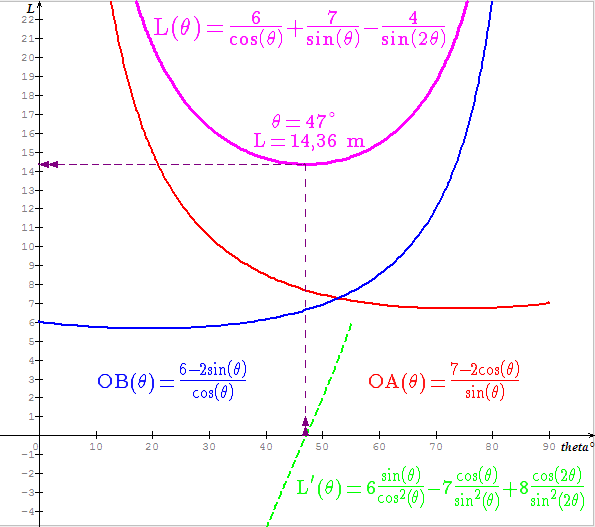
In fine, je m'aperçois que j'ai permuté les valeurs de a et b; celà revient changer t en pi/2 - t et symétriser les courbes ci-dessus par rapport à l'axe vertical t = 45°.
En revanche, la valeur du minimum est inchangée et l'angle t vaut alors 43°.

En espérant ne pas avoir fait d'erreur de raisonnement ou de calcul...

On peut penser que, dans ce cas, le chauffeur parodie Jean Yanne en disant : "Je hais les routes départementales !"



Merci pour cette énigme
.

salut,
je dirais 14m36
merci pour l'énigme

Bonjour,

Je suppose que les roues du camion permettent de glisser pile poil le long des murs.

Il n'est pas précisé dans quelle unité de mesure on doit donner le résultat,
donc en années-lumières, ça donne 0,00 (avec 2 chiffres après la virgule).

Plus sérieusement, j'ai calculé la longueur disponible à 2 mètres du coin en
fonction de l'angle "a" entre le camion et la rue de Mongolie. Ca m'a donné une
expression dont je suis incapable de calculer la racine de la dérivée :

   (6-2.cos a)/sin a + (7-2.sin a)/cos a

J'ai donc cherché cette racine à tatons, et je suis tombé sur :

Longueur maximale du camion : L = 14,36 m

_{En espérant que ma jolie formule est correcte ...}

Bonjour,

Pour continuer son trajet, la longueur maximale du camion doit être de 14,43m.

En prenant pour paramètre la position angulaire A, la longueur maximale du bus que l'on peut 'coincer' dans l'angle du jardin est :

où 0A/2

La longueur maximale permettant au bus de passer est donnée pour l'angle donnant la valeur minimale de l'expression.
Dérivons donc par rapport au paramètre A:







La dérivée s'annule pour A=42°55'26".
Cette valeur d'angle donne la longueur maximale du bus pouvant manoeuvrer dans le coin du jardin, à savoir 14,359m.

ENIGME CLOTUREE

J'ai été très souple dans la correction ... J'ai donné des smileys même à ceux qui ont dit 14,36 alors que le camion ne passerait pas... Puis j'ai donné ThierryMasula même s'il n'a pas répondu à 2 chiffres après la virgule ...

Merci pour votre participation

voir par exemple sur mathcureve:
http://www.mathcurve.com/courbes2d/astroid/astroid.shtml

merci

Bonjour à tous

bonjour à tous
bravo aux courageux(ses)qui ont trouvé la bonne longueur,j'ai reculé devant l'étude de la fonction trigonomètrique

monrow >> pourquoi avoir refusé la réponse de papagon ?

jamo>> cf=14.36133876112909 ... la vraie valeur était 14,3591m

Bonjour Jamo.

papagon fait une approximation en considérant que la longueur maximale du camion est obtenue quand le segment AB a une longueur maximale.
Son approximation n'est pas si mauvaise puisqu'il obtient la bonne réponse (il faut aller au millimètre prés pour voir une différence).

Alors il aurait mieux fait de donner sa réponse finale sans les détails !

jamo>> en effet, puisqu'une démo n'a pas été requise

Bonjour a tous

Joli Mika

merci Epicurien

bonjour, je comprend pas l'erreur de papagon,
(qu'est ce que ca fait du bien de revenir sur l'ile après une semaine de vacances )

je ne comprend pas !
Mon raisonnement est peut être différent des autres mais suffisant pour trouver la valeur demandée : 14.36 m

Salut papagon
Comme j'ai mis la même réponse que toi, c'est pour ça que j'ai demendé ou était ton erreur ...

alors?

Bonjour simon92.

Reprends la figure faite par Papagon.

Il cherche et trouve la position du camion pour laquelle la distance AB est maximale. Il fait alors une faute de raisonnement en considérant que cette position donne aussi pour CD (longueur du camion) la longueur maximale.
Bien sûr, il n'est pas loin de la vérité mais, même en arrondissant au cm inférieur, il est quand même à 1 cm au-dessus de la réponse attendue.

Je pense que le correcteur de l'épreuve a tenu compte de tout cela pour le compter faux.