Inscription / Connexion Nouveau Sujet
Enigme mathématique : oban
Bonjour,
Je vous propose une énigme mathématique.
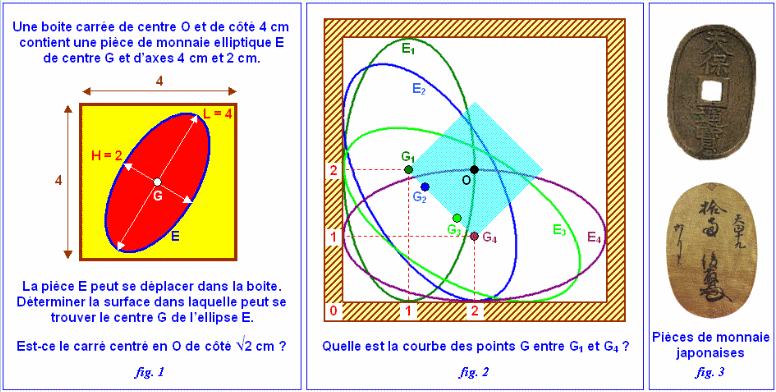
Une boite carrée de centre O et de côté 4 cm contient une pièce de monnaie elliptique E de centre G et d'axes 4 cm et 2 cm (voir fig.1).
La pièce E peut se déplacer dans la boite. Déterminer la surface dans laquelle peut se trouver le centre G de l'ellipse E.
Est-ce le carré centré en O de côté  2 cm ?
2 cm ?
Une autre façon de répondre au problème est de déterminer la courbe des points G entre G1 et G4 (voir fig.2).
Source du problème :
Je me suis inspiré de cet exercice, ainsi que de sa très intéressante correction, paru dernièrement : https://www.ilemaths.net/sujet-tangente-et-ellipse-276986.html
Les pièces de monnaie japonaises de forme elliptique s'appellent "oban" (voir fig.3)
Rudy
Bonjour Rudi,
Je me suis attaqué à ce problème aujourd'hui, par une voie un peu ... détournée.
Au départ je pars d'une ellipse fixe, je prend une tangente en un point, puis une seconde perpendiculaire à la première.
Ces tangentes étant bien sûr les côtés de la boîte.
Tu te doutes bien que le résultat n'est pas un carré. 
J'obtiens quelque chose comme ça: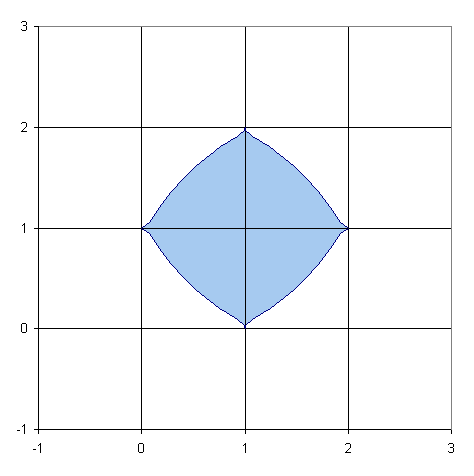
Je détaillerai mes formules plus tard.
A+ 
Bonjour,
Voici donc comment j'ai procédé.
Dans le quart supérieur droit:
Soit x1 l'abscisse d'un point de tangence a l'ellipse.
L'ordonnée,
Soit y = a1x + b1, l'équation de la tangente en (x1,y1).
Distance du centre de l'ellipse à la tangente:
Je ne développe pas avec les x1, y1, ce serait un peu lourd ...
On en déduit l'équation d'une deuxième tangente, perpendiculaire à la première, y = a2x + b2, avec a2 = -1/a1
Avant de calculer b2, cherchons les coordonnées x2 et y2 du 2ème point de tangence.
Enfin, b2 = y2-a2.x2.
Ce qui nous permet de calculer la distance du centre de l'ellipse à la 2ème tangente:
Pour les tois autres quarts de la figure, on adapte un peu les formules de calcul de OH1 et OH2. 
Voilà. Il y avait certainement plus simple et plus élégant, mais bon ...
A+ 
Bonjour gloubi
Je ne trouve pas ce que tu dis
Pour répondre a ta remarque :" Tu te doutes bien que le résultat n'est pas un carré. ", j ai, en effet, un peu "triché" en déplaçant légèrement vers l'origine les centres G2 et G3 des ellipses E2 et E3 afin de laisser croire que c'était un carré...
Tu t'apercevras, en prenant les vrais centres des ellipses, que la figure cherchée n'est pas celle que tu as trouvée, et que sa concavité est opposée à la tienne.
Pour t'en assurer, ne représente qu'une seule ellipse, celle inclinée à 45° : son centre te donnera le point le plus près du point (1,1) : ensuite la figure ayant 4 axes de symétrie, on peut la représenter entièrement.
Reste plus qu'à déterminer les équations des différents arcs de courbe...
Rudy
Bonjour Rudy
Tu as raison !
En prenant une ellipse inclinée à 45°, le point recherché se trouve à l'intérieur de ton "carré".
Je reprendrai mes calculs plus tard...
A+ 
En fait, je cherche, s'il existe, le nom de cette courbe car je pense qu'elle a du être étudiée (pas nécessairement dans le contexte de cette énigme)
Si quelqu'un a des informations ou des liens... merci
Rudy
Coucou !

Dans le cas d'une ellipse de petit axe de longueur nulle (un segment, quoi ...), la figure obtenue est une astroïde.
Dans le cas de cette énigme, comme je me suis vautré lamentablement, je sais pas.
Rudi, la soluce ! 
Bonjour à tous ! 
Voici la courbe obtenu sous geogebra :
Cela ressemble bien à une astroïde...rien d'étonnant car la développée d'une ellipse est une astroïde ayant subie une transformation affine (courbes de Lamé).
Ici c'est néanmoins plus complexe, car il y a du glissement c'est une astroïde "déformée", mais je ne sais pas trop comment ?
C'est peut-être une astroïde toute simple (si le glissement "annule" la transformation) ! 
Allez, je m'y met ! Je pense pouvoir trouver une équation polaire. 
Re-
Et bien voilà ! Après quelque calculs assez énorme, je conclus que cette courbe est formée par 4 arcs de cercles d'angle et de centre les coins de la boîte.
Voici comment j'ai procédé :
Tout d'abord un petit schéma (l'ellipse n'est pas correcte mais ce n'est pas grave) :
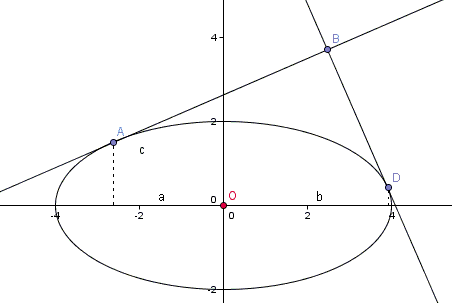
Voici une joli tangente en A d'abscisse a sur le quart supérieur gauche de l'ellipse.
On a l'équation polaire d'un quart de la courbe est .
Reste plus qu'a déterminer f ! 
Pour cela, il faut déterminer la position du point B, et donc l'equation de la tangente en D...
Bref, il nous faut b en fonction de a.
Le coeff directeur de la tangente en x est
d'où la relation :
Ainsi, on trouve
L'ordonnée à l'origine de la tangente en x étant
D'où 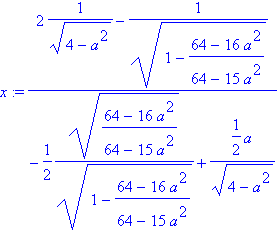
et avec l'équation de tangentes 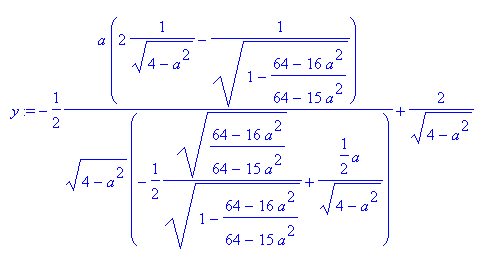
Ainsi, on a
Bon, là je ne peut plus attacher d'image, mais vous vous doutez que l'expression est assez "monstrueuse".
Et on trouve miraculeusement . (merci maple)
Pour déterminer l'angle des arc de cercle on sait que la corde fait \sqrt{2} donc...
oban
Merci à gloubi d'avoir relancé cette énigme dont je n'ai pas retrouvé les brouillons de conception il y a plus d'un mois
Quand je l'ai conçue, je pensais, comme vous, que je tomberais sur une astroïde puisque, par analogie, je considérais le grand axe glissant sur deux axes orthogonaux.
En fait, il n'en est rien, désolé matovitch, les calculs ( que je développerai si besoin ) montrent que l'un des 4 arcs de courbe a pour équation paramétrique :
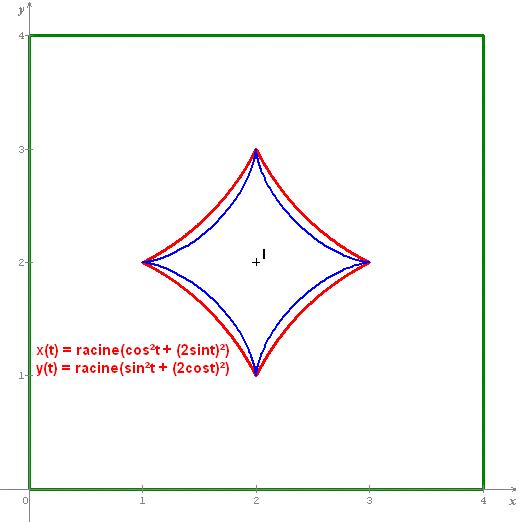
x(t) = racine(cos²t+(2sint)²)
y(t) = racine(sin²t+(2cost)²)
et que les 3 autres arcs sont obtenus par symétries axiales et ponctuelle / I(2,2)
En figure jointe, on voit que l'astroïde équivalente (en bleu) est plus concave que la courbe obtenue (en rouge).
Une autre raison pour laquelle ce n'est pas une astroïde est que les tangentes aux points de rebroussement ne sont ni horizontales ni verticales mais de pente (-2; -1/2; 1/2; 2)
Peut-on établir une équation paramétrique ou polaire pour caractériser cette courbe composée de quatre arcs : si vous y parvenez, merci de me l'indiquer
Je ne sais pas, non plus, si cette courbe a été étudiée et si elle n'a pas été baptisée, cette astrudyoïde (  ) a peut-être des propriétés cachées ?
) a peut-être des propriétés cachées ?
Merci pour vos remarques
Rudy
ah désolé, ma réponse a été rédigée pendant que matovitch envoyait la sienne
je ne pense pas, matovitch, que ce soient des arcs de cercle
bonne soirée
Rudy
je reprends ce que j'ai dit trop rapidement et confirme la proposition de matovitch car, en effectuant x(t)²+y(t)² on trouve bien 5 :
x(t)² + y(t)² = (racine(5))²
ce qui signifie bien que l'arc de courbe élémentaire est un arc de cercle de rayon racine(5), compris entre les points (1;2) et (2;1)
bravo à matovitch
Rudy
Bonsoir Rudi et merci !
Je me suis réveillé un peu tard pour cette très jolie énigme...
Pourrais tu expliquer la méthode générale que tu as employé ?
Je n'ai pas trouvé l'équation polaire de la courbe, mais je vais y réfléchir. 
Bonjour matovich
Voici la méthode que j'ai appliquée :
1- je positionne l'ellipse horizontale dont le centre est en I(2;1) et exprime x(t) et y(t)
2- je l'incline d'un angle a et, par la matrice de rotation, détermine les coordonnées X(t,a) et Y(t,a)
3- je calcule, par X' et Y', les coordonnées du point le plus bas et de celui le plus à droite de l'ellipse inclinée
4- j'en déduis le vecteur de translation du centre I afin que l'ellipse inclinée soit tangente aux côtés de la boîte
5- en faisant varier a de 0 à pi/2, j'exprime les coordonnées du centre de l'ellipse en fonction de a et obtiens le tronçon sud-est.
6- par symétries axiales et ponctuelle, j'obtiens les 3 autres tronçons
Rudy


