Inscription / Connexion Nouveau Sujet
Enigmo 232 : Traversée hasardeuse
Bonjour tout le monde,
pour fêter la Chandeleur, notre brave Homer a abusé du cidre !
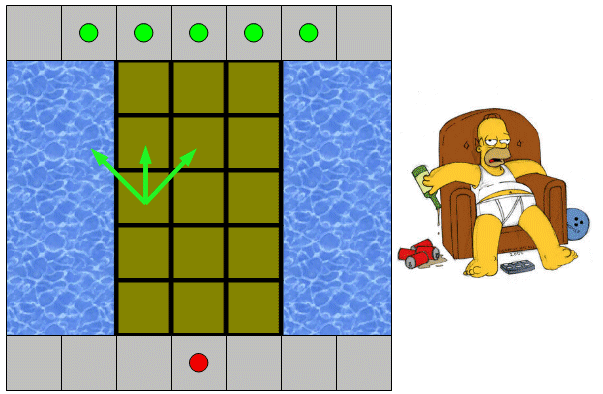
Pour rentrer chez lui, il doit traverser un petit pont, représenté sur la figure ci-dessous.
Il part du point rouge de la rive du dessous et doit rejoindre la rive du dessus, sur l'un des points verts.
Par contre, étant donné son état d'ébriété avancé, sa manière de se déplacer est un peu particulière.
Quand il est sur une case, son prochain pas peut le conduire à l'une des 3 cases située au dessus : celle directement au-dessus, et celles situées au-dessus à droite et à gauche (ces 3 possibilités sont schématisées par les 3 flèches vertes).
Chacun des trois déplacements possibles a une probabilité de 1/3.
Le pont a une largeur de 3 cases et une longueur de 5 cases, et s'il est sur un bord et qu'il fait un pas du mauvais côté, il tombe à l'eau et c'est terminé !
Rappelons que le départ se fait du point rouge et que les cases d'arrivée possibles sont celles qui contiennent un point vert.
Question : quelle est la probabilité qu'Homer arrive sain et sauf sur l'autre rive ?
Je veux la valeur exacte pour la probabilité, c'est-à-dire un nombre entre 0 et 1, sous la forme d'une fraction irréductible ou d'un décimal si elle tombe juste.
Bonne recherche ! 
 Bonjour Jamo,
Bonjour Jamo,
La probabilité que Homer arrive sain et sauf sur l'autre rive (hors cirrhose foudroyante, écroulement du pont, attaque de mouettes ...) est à mon avis :
 Bonjour,
Bonjour,
Je trouve que le brave Homer a une probabilité
d'arriver sur un des 5 plots verts de 0.2846
 Bonjour Jamo.
Bonjour Jamo.
La probabilité est 11/27.
Méthode :
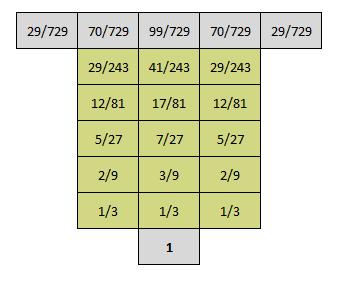
dans chaque case, on inscrit le nombre de façon d'y arriver sans être tombé dans la rivière auparavant; les premières cases contiennent 1; chaque autre case contient la somme des nombres se trouvant au-dessous d'elle, directement ou en diagonale
on inscrit donc successivement :
1 1 1
2 3 2
5 7 5
12 17 12
29 41 29
(29+41+29)/35 = 11/27
 Bonjour,
Bonjour,
La probabilité qu'Homer arrive sain et sauf sur l'autre rive est de 11/27.
Explication : On remplit simplement un tableau des probabilités d'arriver sur chaque case atteignable (voir schéma ci-dessous). La somme des cases d'arrivée fournit la probabilité cherchée.
 Bonjour/Bonsoir,
Bonjour/Bonsoir,
Je pense que Homer a 11/27 chances d'arriver sur un point vert.
... qui ne sera juste que si ce raisonnement l'a été ...
La probabilité d'aller sur une des cases suivantes (y compris à coté du pont) étant de 1/3, la probabilité d'arriver sur une case est la somme du tiers des probabilités d'être arrivé sur une des cases y menant.
Avec :
i=0 l'indice de la ligne du point rouge,
i=6 celui de la ligne des points verts,
B(i) la probabilité d'arriver sur une case du bord du pont,
M(i) celle d'arriver sur une case du milieu du pont,
P(i) la probabilité d'arriver sur la ligne i du pont,
on a par récurrence :
B(0) = 0 ; M(0) = 1 ; (position de départ d'Homer)
B(n+1) = B(n)/3 + M(n)/3 ; (deux cases y mènent)
M(n+1) = 2*B(n)/3 + M(n)/3 ; (trois cases y mènent)
P(n+1) = 2*B(n+1) + M(n+1) = 4*B(n)/3 + M(n) = P(n) - 2*B(n)/3
La probabilité d'arriver sur les points verts est égale à celle d'arriver sur les cases de la ligne 5 du pont, soit P(5)=2*B(5)+M(5).
Ce qui donne, avec B(5)=29/243 et M(5)=41/243, le résultat :
(41 + 2*29) / 243 = 99/243 = 11/27 proche de 40,74%.
Merci pour vos énigmes.
 Oops, j'ai indiqué par mégarde ces chances de finir à l'eau : la probabilité recherchée est donc 99/243
Oops, j'ai indiqué par mégarde ces chances de finir à l'eau : la probabilité recherchée est donc 99/243
 Bonjour,
Bonjour,
en raisonnant avec un "arbre de probabilité", on obtient une probabilité de 11/27 pour que Homer arrive sain et sauf sur l'autre rive.
il a une probabilité de 29/729 d'arriver sur les cases extérieures, de 70/729 sur les 2èmes cases,et de 99/729 sur la case centrale. Cela fait une probabilité totale de 297/729qui se simplifie en 11/27.
La probabilité qu'il tombe à l'eau est un peu plus grande, elle est de 16/27 (soit 216/729).
Pauvre Homer, il ne faut pas abuser de la bière, tu as de grandes chances de ne pas passer le pont..
 je pense qu'il faut faire:
je pense qu'il faut faire:
7/9 puissance 4 car à chaque fois, il a une chance de tomber à gauche et une chance de tomber à droit pour 7 chance de rester de rester sauf au premier où il reste obligatoirement sue le pont.
Ca fait 2401/6561
 Bonjour
Bonjour
Je crains que notre pauvre Homer ait plus de chances de finir à l'eau qu'au sec !
En effet, d'après mes calculs il n'aurait qu'une probabilité de 11/27 d'arriver sain et sauf.
merci et à bientôt
 Bonjour Jamo,
Bonjour Jamo,
sauf erreur
nombre de parcours 340
nombre de chutes possibles 40
p=300/340=15/17
merci pour l' énigme
 Bonjour,
Bonjour,
sauf erreurs de calcul, la probabilité qu'Homer arrive sain et sauf est 11/27.
Une petite généralisation pour un pont de longueur n et de largeur 3 en modélisant le problème par une chaine de Markov et en diagonalisant sa matrice de transition:
la probabilité qu'Homer arrive sain et sauf est
cette formule doit pouvoir se simplifier mais Maple n'y arrive pas directement et je n'ai pas le courage de le faire à la main  ...
...
Merci pour l'énigme  ,
,
1emeu
 Bonjour,
Bonjour,
Voici ma réponse :
La probabilité qu'Homer arrive sain et sauf sur l'autre rive est .
Démonstration :
Considérons un graphe stochastique à 4 états où l'état 1 est la case de gauche sur le pont, l'état 2 est la case du milieu, l'état 3 est la case de droite et l'état 4 est l'eau. On a alors la matrice de transition suivante :
Considérons que le pont soit constitué de 5 lignes, on note
où est la proababilité q'Homer se trouve à l'état i à la ligne n.
On a donc
et la relation de récurrence
Avec cela on calcul . On a
Ainsi la probabilité cherchée est
Merci.
 Bonjour,
Bonjour,
La probabilité qu'a Homer d'arriver sain et sauf est de
On peut plus généralement calculer cette probabilité pour un pont de longueur quelconque :
Pour un pont de longueur supérieure à 12 Homer a moins d'une chance sur 10 d'arriver au bout, et à partir d'une longueur supérieure à 22 il a moins d'une chance sur 100 
Merci pour l'énigme 
 bonjour,
bonjour,
j'ai trouvé 105/243=0.43 soit 43% de chance d'arriver à bon port (je ne suis pas très sur)
merci
 Salut tout le monde.
Salut tout le monde.
Plus généralement, pour une longueur de n cases, et pour la même largeur de pont, la probabilité est:
Pn=(3/2)*{[(1+ 2)/3]n+1+[(1-
2)/3]n+1+[(1- 2)/3]n+1}
2)/3]n+1}
Ici, n=5 et on trouve P5=11/27
La notion principale à connaître est celle des suites de Fibonacci.
La relation de récurrence de second ordre à trouver nécessite par ailleurs une capacité à savoir jongler avec les différentes suites immédiatement reliées à ce problème.
Quelques vérifications sont rassurantes:
D'abord, Pn 1 pour tout n de
1 pour tout n de *.
*.
Ensuite, P0=P1=1, ce qui est cohérent si la longueur est 0 ou 1.
De plus, Pn est décroissante, ce qui est convainquant.
Enfin, bien noter qu'évidemment, Pn est de plus en plus proche de 0 à mesure que n grandit, ce qui est naturel:
Plus le pont est long, et moins le pauvre Homer peut espérer traverser le pont sain et sauf.
PS:
La longueur n=5 est bien choisie: ce n'est en effet qu'à partir de n=5 que Pn devient inférieure à 50%
P4=41/81 > 0,5 et P5=11/27 < 0,5.
Hasard?
 Bonjour,
Bonjour,
La probabilité qu'il réussisse est d'exactement 11/81 (moins d'une chance sur 7, aïe aïe aïe !!!)
Clôture de l'énigme
La bonne réponse était : 11/27.
Pour résoudre ce petit problème de probabilités, on pouvait y arriver avec un peu d'organisation en écrivant la probabilité pour chaque case, puis en finissant par quelques additions.
Pour approfondir, on peut aussi établir les formules qui donnent les probabilités pour chaque case. On tombe sur un petit système différentiel qu'il est possible de résoudre et on peut même exprimer les formules générales en fonction du nombres de pas effectués.
Bref, bravo à ceux qui ont trouvé la bonne réponse, et pour certain d'entre vous, revoyez vos calculs, il doit y trainer quelques petites erreurs.
Je me suis dit qu'il y avait un piège car cette énigme est notée 3 étoiles,et j'aurais dû quand même jouer car j'avais la bonne réponse !
Je ferais sûrement les énigmes de mars,mais plus celles de février (j'arrive trop tard  ) ou peut-être encore celle de TRON.
) ou peut-être encore celle de TRON.
Nombre de participations : 0
Temps de réponse moyen : 89:38:18.

 bien mérité :
bien mérité :

 0.894
0.894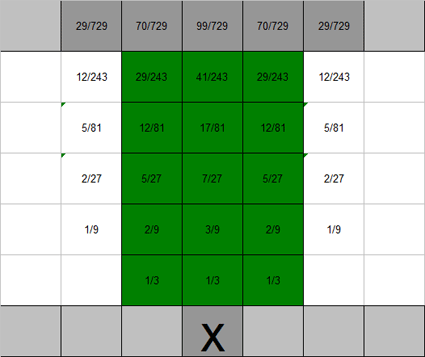
 à tous, très intéressant.
à tous, très intéressant.

 jamo
jamo
