Inscription / Connexion Nouveau Sujet
Enigmo 248 : Chemin dans un triangle de nombres
Bonjour tout le monde,
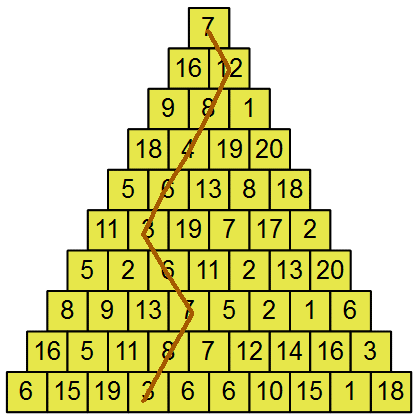
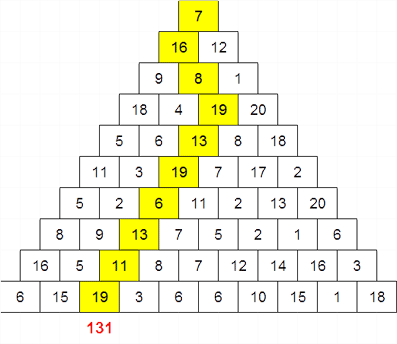
on donne ci-dessous une série de nombres disposés en triangle (les nombres sont aléatoires, n'y cherchez aucune particularité).
Voici comment on se déplace dans ce triangle :
- le point de départ est le sommet du triangle, c'est-à-dire la case 7 ;
- à chaque étape on descend d'un étage dans une des deux cases voisines avec la précédente ;
- le point d'arrivée est une des cases de la ligne inférieure.
Un chemin est donc constitué de 10 étapes.
Sur la seconde figure, j'ai représenté un tel chemin en rouge, et si on additionne les 10 nombres de ce chemin, on trouve un total de 110 (si je ne me suis pas trompé dans l'addition).
Question : Trouver le chemin qui permet d'obtenir la somme maximale.
Pour la réponse, vous me donnerez le total obtenu, puis la liste des 10 cases du chemin.
De plus, mais ce n'est pas obligatoire, vous pourrez expliquer la méthode employée, je pense que cela sera aussi intéressant.
Bonne recherche ! 


 Bonjour Jamo
Bonjour Jamo 
total: 131
7-16-8-19-13-19-6-13-11-19
Sans aucune méthode  , juste une impression visuelle.
, juste une impression visuelle.
 Bonjour!
Bonjour!
Allez, je vais tenter de répondre à ma première énigme, avec l'espoir que ça passe...
Je n'ai pas cherché plus que cela, mais je propose:
Total: 131, avec les cases: 7,16,8,19,13,19,6,13,11,19.
Pour ce qui est de ma méthode, elle est, disons, un peu à tâtons.
J'ai commencé par calculer la somme des nombres maximums de chaque ligne: 157.
Ensuite, j'ai regroupé les lignes par 2, et calculé les maximums "atteignables" de chaque groupe, dans l'ordre: 23,27,35,26,31 et en notant quand même que pour les trois derniers, on pouvait faire 32,19 et 30, relativement acceptable dans le contexte.
J'ai ensuite mis en évidence ces groupes sur le dessin:
(Dessin que je n'arrive pas à mettre en ligne....)
Mais bref, on voyait clairement un chemin se détacher (celui que je propose), qui prenait les 2 premiers groupes maximums et les 3 groupes acceptables, j'ai fini par quelques essais en essayant de lier tout les groupes maximums entre eux, quitte à perdre un peu sur le score, mais je trouvais à chaque fois un nombre inférieur, et donc je propose celui-ci, on verra!
 Bonjour jamo,
Bonjour jamo,
Je propose un total de
131
Trajet
7, 16, 8, 19, 13, 19, 6, 13, 11, 19.
Merci pour l'Enigmo 
 Bonjour, je propose le chemin suivant dont la somme fait 131:
Bonjour, je propose le chemin suivant dont la somme fait 131:
Case 7 /16/8/19/13/19/6/13/11/19
J'ai procédé par déduction en partant de la case numéro 19 et d'étudier les sommes les plus conséquentes en remontant la chaine.
 Bonjour
Bonjour
Je drais 131 = 7 + 16 + 8 + 19 + 13 + 19 + 6 + 13 + 11 + 19
A l'intuition , au pif , à la chance ou à la malchance .
Sans doute un  supplémentaire.
supplémentaire.
Voici en image
A+

 Bonjour,
Bonjour,
voici une solution en image:
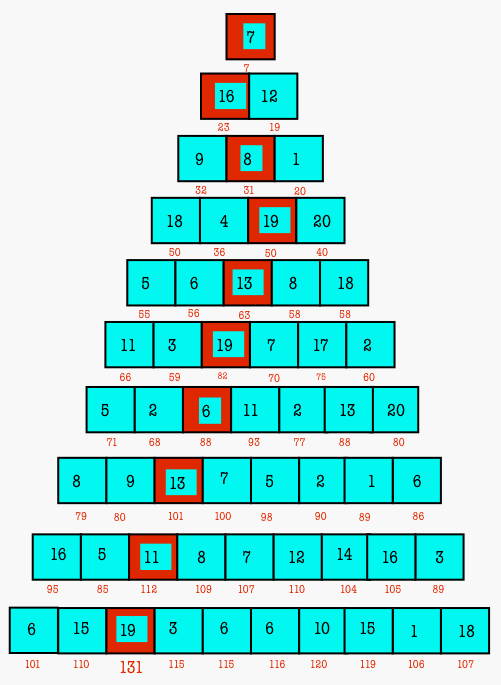
Le chemin qui donne le résultat maximum est en rouge et le total vaut 131
La méthode est très simple: en partant de la case de tête, on descend et pour chaque case on totalise la valeur de cette case avec les deux cases supérieures adjacentes; on garde la valeur maximale. De ligne en ligne, on arrive à la ligne inférieure avec les totaux maximaux. Pour déterminer le chemin parcouru, il suffit de remonter en déduisant la valeur de la case inférieure. Voir les valeurs calculées en rouge sur le dessin
Bien à vous
 Bonjour,
Bonjour,
J'ai décomposé le grand triangle en plusieurs petits triangles puis déterminé pour tous ces petits triangles quel serait le meilleur chemin.
Ensuite, avec le ré-assemblage de ces derniers, j'obtiens que le meilleur total est de 131.
La suite de cases : 7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19 ( 3*19+16+2*13+11+8+7+6 = 131 )
Bonne journée.
JeaMachine.

 Salut,
Salut,
Mon total est de 131
Chemin : 7 16 8 19 13 19 6 13 11 19
(Méthode : Programme en VBA qui a exploré toutes les possibilités)
 Bonjour,
Bonjour,
Je trouve 131
7 16 8 19 13 19 6 13 11 19
en privilégiant le meilleur total de la ligne n-1 qui permet le meilleur total de la ligne n+1
 Pour le total j'obtiens 131 en passant par les cases
Pour le total j'obtiens 131 en passant par les cases
7
16
8
19
13
19
6
13
11
19
Personnellement, j'ai ciblé les nombres au-dessus de la dizaine, trouvé des chemins potentiellement forts et parmi ces chemins, j'ai comparé les valeurs des sommes.
Les trois 19 dans la même diagonale, assortis d'un 11 et de deux 13 m'ont tapé dans l'œil.
Avec d'autres nombres j'aurai probablement procédé autrement !
 Bonjour Jamo,
Bonjour Jamo,
Somme maximale: 131
Pour la liste,voici une image

Méthode: par programmation en Qbasic:
DECLARE SUB Init ()
DECLARE SUB Chemin (way AS STRING, som AS INTEGER)
DECLARE SUB Gauche (way AS STRING, som AS INTEGER)
DECLARE SUB Droite (way AS STRING, som AS INTEGER)
DECLARE FUNCTION numDiag% (x AS INTEGER)
DECLARE FUNCTION numGauche% (x AS INTEGER)
DECLARE FUNCTION Net2$ (x AS INTEGER)
DECLARE FUNCTION numDroite% (x AS INTEGER)
CONST n = 10
CONST Maxi = n * (n + 1) / 2
CONST Faux = (0 = 1)
CONST Vrai = NOT (Faux)
DATA 7
DATA 16,12
DATA 9,8,1
DATA 18,4,19,20
DATA 5,6,13,8,18
DATA 11,3,19,7,17,2
DATA 5,2,6,11,2,13,20
DATA 8,9,13,7,5,2,1,6
DATA 16,5,11,8,7,12,14,16,3
DATA 6,15,19,3,6,6,10,15,1,18
DIM SHARED Galton(Maxi) AS INTEGER
DIM SHARED som0 AS INTEGER, way0 AS STRING
DIM SHARED Diag(n) AS INTEGER
CLS
OPEN "c:\_enigmo\248\248.txt" FOR OUTPUT AS #1
CALL Init
CALL Chemin("01", 7)
LOCATE 20, 1
PRINT " fin du programme"
CLOSE #1
END
SUB Chemin (way AS STRING, som AS INTEGER)
IF LEN(way) < 19 THEN
CALL Gauche(way, som)
CALL Droite(way, som)
ELSE
PRINT #1, way; ","; som
IF som0 < som THEN
som0 = som
way0 = way
LOCATE 4, 1: PRINT way0, som0
END IF
END IF
END SUB
SUB Droite (way AS STRING, som AS INTEGER)
SHARED Galton() AS INTEGER
DIM num AS INTEGER, g AS INTEGER
DIM w AS STRING, s AS INTEGER
w = way
s = som
num = VAL(RIGHT$(w, 2)): ' le noeud
g = numDroite%(num)
w = w + Net2$(g)
s = s + Galton(g)
CALL Chemin(w, s)
END SUB
SUB Gauche (way AS STRING, som AS INTEGER)
SHARED Galton() AS INTEGER
DIM num AS INTEGER, g AS INTEGER
DIM w AS STRING, s AS INTEGER
w = way
s = som
num = VAL(RIGHT$(w, 2)): ' le noeud
g = numGauche%(num)
w = w + Net2$(g)
s = s + Galton(g)
CALL Chemin(w, s)
END SUB
SUB Init
SHARED Galton() AS INTEGER, som0 AS INTEGER, way0 AS STRING, Diag() AS INTEGER
DIM i AS INTEGER
som0 = 0
way0 = ""
RESTORE
FOR i = 1 TO Maxi
READ Galton(i)
NEXT i
FOR i = 1 TO n
Diag(i) = i * (i + 1) / 2
NEXT i
END SUB
FUNCTION Net2$ (x AS INTEGER)
Net2$ = RIGHT$("00" + LTRIM$(STR$(x)), 2)
END FUNCTION
FUNCTION numDiag% (x AS INTEGER)
SHARED Diag() AS INTEGER
DIM i AS INTEGER
i = 1
WHILE Diag(i) < x
i = i + 1
WEND
numDiag% = i
END FUNCTION
FUNCTION numDroite% (x AS INTEGER)
numDroite% = numGauche%(x) + 1
END FUNCTION
FUNCTION numGauche% (x AS INTEGER)
SHARED Diag() AS INTEGER
DIM lig AS INTEGER, col AS INTEGER, i AS INTEGER
lig = numDiag%(x)
col = lig - (Diag(lig) - x)
numGauche% = (lig + 1) * lig / 2 + col
END FUNCTION
SUB Visu
SHARED Galton() AS INTEGER
DIM i AS INTEGER, j AS INTEGER, k AS INTEGER
FOR i = 1 TO n
FOR j = 1 TO i
k = i * (i - 1) / 2 + j
PRINT Galton(k); " ";
NEXT j
PRINT " "
NEXT i
END SUB
Réponse: 01020509131824313948, 131
Merci pour l'énigmo.
 On trouve un total de 131 et le chemin suivant :
On trouve un total de 131 et le chemin suivant :
7
16
8
19
13
19
6
13
11
19
Je me suis contenté des tester toutes les possiblités à l'aide de Maple.
Voici le programme s'il vous intéresse :
> reponse:=proc(M)
> local Max, S, E, i2, i3, i4, i5, i6, i7, i8, i9, i10;
> E:=array(1..10);
> Max:=0;
> E[1]:=M[1,1];
> for i2 from 1 to 2 do
> for i3 from i2 to i2+1 do
> for i4 from i3 to i3+1 do
> for i5 from i4 to i4+1 do
> for i6 from i5 to i5+1 do
> for i7 from i6 to i6+1 do
> for i8 from i7 to i7+1 do
> for i9 from i8 to i8+1 do
> for i10 from i9 to i9+1 do
> S:=M[1,1]+M[2,i2]+M[3,i3]+M[4,i4]+M[5,i5]+M[6,i6]+M[7,i7]+M[8,i8]+M[9,i9]+M[10,i10];
> if S>Max then
> Max:=S;
> E[2]:=M[2,i2];
> E[3]:=M[3,i3];
> E[4]:=M[4,i4];
> E[5]:=M[5,i5];
> E[6]:=M[6,i6];
> E[7]:=M[7,i7];
> E[8]:=M[8,i8];
> E[9]:=M[9,i9];
> E[10]:=M[10,i10];
> end if;
> end do;
> end do;
> end do;
> end do;
> end do;
> end do;
> end do;
> end do;
> end do;
> return E;
> end proc;
M est la matrice triangulaire inférieure formée par les coefficients de la pyramide.
 Bonjour,
Bonjour,
Le meilleur total atteignable est de 131, avec le chemin suivant :
7, 16, 8, 19, 13, 19, 6, 13, 11, 19.
La méthode :
On construit un triangle "max" similaire à celui de départ.
On le remplit de bas en haut.
Dans chaque case du triangle max, on additionne le nombre qui figurait dans le triangle de départ, avec le plus grand des deux nombres inscrits dans les cases inférieures du triangle max.
Le schéma ci-dessus explique ça bien mieux que moi  ...
...
Par ce procédé, chaque case du triangle max contient le plus grand total atteignable entre cette case et la base (chaque case est donc un extremum partiel).
Au sommet de ce triangle figure donc la solution cherchée.
Pour reconstituer le chemin parcouru pour arriver à cet optimum, c'est assez simple :
on redescend du sommet en cherchant simplement la case du triangle de départ qui permet de passer d'un extremum à l'autre.
Sauf erreur, un très ancien souvenir de recherche opérationnelle me souffle que c'est le théorème de Bellman qui permet cette simplification.
 Bonjour !
Bonjour !
(ça faisait longtemps...)
Sauf erreur de recopiage des nombres, le chemin maximal "pèse" 131, que l'on obtient en suivant le chemin:
7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19
pour obtenir ce résultat il suffit de prendre le problème à l'envers:
c'est le principe de la programmation dynamique (dite de "Bellman")
- on dessine un triangle vide de la même taille.
- on copie la dernière ligne du triangle original dans la dernière ligne du triangle vide.
- dans chaque case de l'avant-dernière ligne, on indique le nombre original + le plus grand des deux nombres se trouvant dans les deux cases inférieures (donc : 16 + max(6,15) = 31 pour la première case de l'avant-dernière ligne).
- on remonte d'une ligne et on recommence (donc : 8 + max(31,24) = 39 pour la première case de l'antépénultième ligne...)
- on arrive au sommet avec le maximum de 131.
- il suffit ensuite de "détricoter" ce maximum pour retrouver la séquence...
merci pour l'énigme !!
 Bonjour,
Bonjour,
Le total obtenu est: 131.
La liste des 10 cases du chemin est representee, ci-dessous, en rouge.

Je n'ai pas pour l'instant de preuve precise permettant de resoudre le probleme.
Merci pour l'enigmo.
 Bonjour Jamo,
Bonjour Jamo,
Je propose un total de 131
7 16 8 19 13 19 6 13 11 19 => Total de 131
Je décris les méthodes dans un autre post
Et encore et toujours un grand merci pour tous tes efforts pour nous divertir
A+
 Re-bonjour Jamo,
Re-bonjour Jamo,
J'ai utilisé deux techniques totalement différentes (sans programmation...pour le sport)
(1)Avec MS Project
J'ai pris l'analogie suivante :
- une étape d'un projet = un certain nombre de jours de travail
- chaque étape est suivie par une ou plusieurs autres
- l'enchainement le plus long (= la durée totale du projet) est ce qu'on appelle le chemin critique
==> j'ai encodé les différentes durées (les valeurs des différentes cases) et leurs liens (schéma très répétitif facile à encoder)
==> le chemin critique (Network View) donne notre enchaînement au total maximum
(2) dans une feuille de calcul Excel
- chaque succession d'étape coorespond à un choix binaire Gauche-Droite qui peut être codé 0-1
- tous les chemins possibles sont dès lors générés en cod
 Oups...tapé trop vite...
Oups...tapé trop vite...
SUITE
2) dans une feuille de calcul Excel
- chaque succession d'étape dans le triangle correspond à un choix binaire Gauche-Droite qui peut être codé 0-1
- tous les chemins possibles sont dès lors générés en codant les chiffres décimaux de 0 à 511
- la somme des chiffres binaires à gauche de chaque position de chaque nombre binaire donne son rang sur chaque ligne
==> cela permet de retrouver sa valeur via un VLOOKUP dans le tableau de base
- le max du total de chaque série donne le nombre cherché et le chemin pour y arriver
Cette deuxième méthode semble compliquée dans sa description, mais le principe est super simple...
Par programmation via un tableau c'est bien sur plus rapide...
Je suis curieux de voir les autres techniques utilisées...
A+
 Bonjour Jamo,
Bonjour Jamo,
Je proposerais volontiers un total de 131 : 7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19 .
Méthode : aucune, simple coup d'oeil.
 Bonjour,
Bonjour,
somme maximale : 131
cases : 7, 16, 8, 19, 13, 19, 6, 13, 11, 19.
Méthode empirique en première approche : étant sur une case, je cherche si il y a un chemin supérieur aux autres sur les 2 lignes suivantes.
Étant sur 7 (Ligne 1), 16 (L2) puis 8 ou 9 (L3) sera supérieur à 12 (L2) puis 8 (L3) donc je vais sur 16 (L2).
Étant sur 16 (L2), 9 (L3) puis 18 (L4) est un chemin équivalent à 8 (L3) puis 19 (L4) , je vais donc une ligne plus loin et je vois que 8 (L3) et 19 (L4) permet d'accéder à 13 (L5) bien supérieur aux voisins.
Remarque : On continue comme ça, ce qui va très vite, et on peut regretter que cette méthode empirique un peu simpliste soit suffisante pour trouver la solution.
Autre méthode à laquelle j'ai pensé pour vérifier la solution : dire que chaque case est un nœud, définir les chemins existants ayant le coût du nœud
d'arrivée. (concrètement, L1 permet d'aller en L2(1) avec un coût de 16 et en L2(2) avec un coût de 12. ...)
On ajoute que chaque nœud de la ligne 10 permet d'atteindre la case d'arrivée avec un coût de 0.
Il ne reste plus qu'à chercher le chemin maximal reliant départ et arrivée avec la théorie des graphes. (Petite remarque en passant : si on veut utiliser un algorithme fournissant le chemin minimal, il suffit de remplacer chaque valeur N de case par 20-N et le chemin maximal du premier triangle devient le chemin minimal du second).
Il faut bien reconnaître que si la méthode est imparable, elle va être assez lourde à mettre en œuvre  .
.
Et enfin, la force brute. Il suffit d'écrire une petite macro qui balaye toutes les possibilités (il n'y en a guère que 2 puissance 9 !). Certes peu glorieux, mais immédiat.
Pour le même prix, cette macro nous fournit aussi le chemin minimal :
total 64
cases 7, 12, 8, 4, 6, 3, 6, 7, 8, 3.
Merci pour l'énigme.
Cordialement.
 Bonsoir jamo ,
Bonsoir jamo ,
Total obtenu pour les 10 cases du chemin = 131
Le chemin qui permet d'obtenir C :
7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19.
Méthode employée :
Pour obtenir la somme maximale je pars de la base et remonte le triangle de cette façon :
premier étage : 16 est en commun avec 6 et 15 , donc je retiens 15. 16 est donc remplacé par 31 (16+15)
puis 5 a en commun avec 15 et 19 , donc je retiens 19. 5 est donc remplacé par 24 (5+19)
donc identique .......jusqu'à 3.
deuxième étage : 8 a en commun maintenant avec 31 et 24,, donc je retiens 31. 8 est donc remplacé par 39 (8+31)
..........
neuvième étage : 7 a en commun maintenant avec 124 et 120,, donc je retiens 124 et 7 est remplacé par 131 (7+124)
Pour le chemin je décline le nouveau triangle créé : 131 = 7
131-7=124 ( 16 )
124-16 =108 (8)
108-8 = 100 (19)
.......
30-11=19
Merci .
 Bonjour tout le monde
Bonjour tout le monde
Je propose: 7+16+8+19+13+19+6+13+11+19 = 131
Il y'a 512 possibilités (2^9)et je l'ai fait par exel
 Salut Jamo,
Salut Jamo,
Je propose une somme maximale de 131.
Cette somme est composée des cases suivantes :
7;16;8;19;13;19;6;13;11;19
Merci.
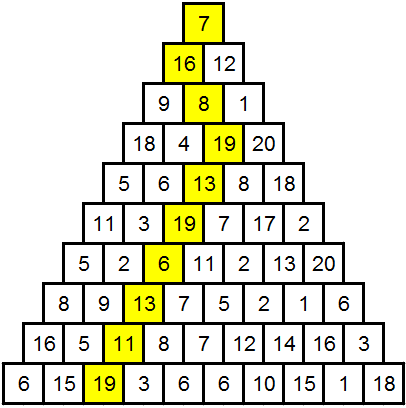
 bonjour,
bonjour,
c'est le xième essai d'envoi (je vois apparaitre :préciser un forum valide ?)j'espère que ce sera le dernier
je trouve 131 comme maximum avec comme chemin correspondant
7
16
8
19
13
19
6
13
11
19
merci pour cet enigmo
 pour moi, le max c'est 131 (sauf erreur de calcul)
pour moi, le max c'est 131 (sauf erreur de calcul)
en faisant :
7 16 8 19 13 19 6 13 11 19
J'ai procédé en "remontant", par la base : j'ai remplacé les deux dernières lignes par une seule ligne de 9 cases, avec dans chaque case le plus grand nombre obtenu en additionnant les nombres des deux dernières lignes, exemple case tout en bas à gauche :
les deux lignes donnent :
16
6 15
j'ai donc le choix entre 16+6=21 et 16+15=31, je choisis évidemment 31 et j'écris cela dans ma nouvelle case en bas à gauche, en faisant de même pour toute la ligne, je me suis ramenée à un pb de 9 lignes au lieu de 10, et je recommence, etc.
 Bonjour et merci pour cette énigme,
Bonjour et merci pour cette énigme,
Je trouve un maximum de 131 avec la suite de nombres de l'image (pardon c'est moche mais c'est paint aussi).
Pour trouver j'ai juste cherché à la main.
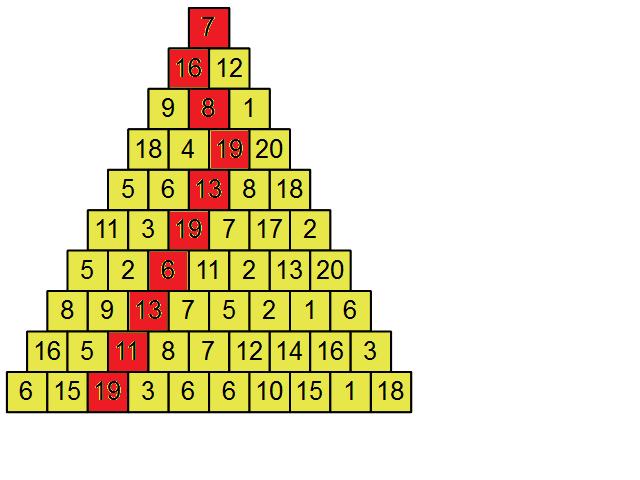
 Bonjour,
Bonjour,
La solution est en image : et je trouve une somme maximale de 131.
La méthode employée (pas forcément la plus rapide après coup), c'est une résolution par ordinateur. Le programme parcours toutes les combinaisons, et retiens la plus élevées.
PS : si ça intéresse la somme la plus faible est de 64 : 7 12 8 4 6 3 6 7 8 3
 Bonjour jamo,
Bonjour jamo,
Un total de 131 avec la séquence:
7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19
La méthode utilisée ?
Un tableau sous Excel (512 lignes).
Avec les copiés-collés, c'est relativement rapide, d'autant qu'au bout de 7 nombres j'ai un total max pour la suite 7 - 16 - 8 - 19 - 13 - 19 - 6 et que les 13, 11, 19 qui suivent font largement le compte.
Merci pour l'énigme ! 
 Bonjour jamo !
Bonjour jamo !
Allez, je tente.
Je trouve une somme maximale de 127, qui s'obtient en faisant la somme suivante : 7+12+1+20+18+12+20+6+16+15.
A+ et merci pour l'énigme !
 Bonjour,
Bonjour,
Je trouve un maximum de 131 avec le chemin suivant :
7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19
méthode utilisée : tâtonnement 
Merci pour cette énigme
 Je trouve une somme maximale de 131 en suivant le chemin suivant :
Je trouve une somme maximale de 131 en suivant le chemin suivant :
7 - 16 - 8 - 19 - 13 - 19 - 6 - 13 - 11 - 19
Je trouve ce résultat grâce à un tableau excel où après chaque ligne, en fonction de la case sur laquelle je tombe je garde la somme maximale intermédiaire.
Merci pour l'énigme en tout cas 
 Bonsoir ou bonjour,
Bonsoir ou bonjour,
Je dirais: 7-16-8-19-13-19-6-13-11-19
La somme fait donc 131 sauf erreur.
Pour la méthode à part comparer les nombres d'une même ligne, je n'en avais pas vraiment 
Encore merci pour ces énigmes!
 Bonjour,
Bonjour,
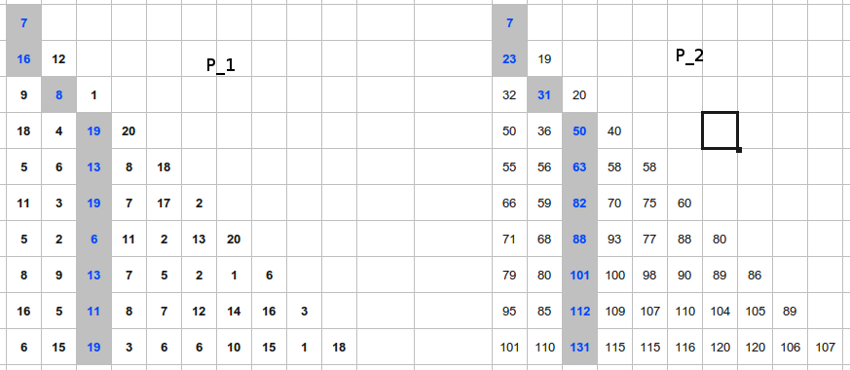
pour répondre à cette énigme, j'ai utilisé un tableur.
J'ai d'abord entré les valeurs de la pyramide (pyramide p_1), puis j'ai construit à coté une pyramide (pyramide p_2) dont chaque brique contient la valeur de la brique équivalente de p_1 plus la valeur la plus grande des deux briques mères côté p_2
Il suffit de partir de la dernière ligne de p_2, choisir la plus grande valeur, puis remonter de ligne en ligne en choisissant toujours la valeur le plus grande pour la brique mère. On fait le chemin identique sur P_1 pour avoir la réponse :
La suite est donc : 7-16-8-19-13-19-6-13-11-19 pour une somme de 131
 Bonjour Jamo.
Bonjour Jamo.
7 + 16 + 8 + 19 + 13 + 19 + 6 + 13 + 11 + 19 = 131
gauche, droite, droite, puis gauche six fois de suite
 Bonsoir jamo
Bonsoir jamo  ,
,
Je tente.
Je propose comme total maximal 131.
Liste des 10 cases du chemin : 7-16-8-19-13-19-6-13-11-19. En image :

Ma méthode (si on peut l'appeler ainsi) est celle-ci : J'ai cherché le plus grand nombre contenu dans une des cases d'arrivée, puis je suis remonté et au fur et à mesure que je rencontrais les deux cases au-dessus de la précédente, je prenais celle qui comprenait le plus grand nombre jusqu'à arriver à 7 qui est la case de départ. J'ai obtenu 131 et je me suis dit alors qu'il devait être le nombre maximal. Bien sûr, après j'ai essayé avec des nombre plus petits que 19 mais je n'ai pas trouvé mieux. Et là, j'ai arrêté.
Je n'ai pas utilisé de logiciels, on verra le résultat à la fin.
Merci pour l'énigme  .
.
À plus  !
!
 Je propose le chemin :
Je propose le chemin :
7; 16; 8; 19; 13; 19; 6; 13; 11; 19 avec un total de 131.
Pour la méthode employée, j'ai tenté le calcul manuel. Quand j'ai dépassé les 4 pages  , je me suis dit que l'ordi servait à quelque chose
, je me suis dit que l'ordi servait à quelque chose  Et une fois faite la transformation du triangle en arbre (un peu longue), un petit algo récursif me donne ce résultat.
Et une fois faite la transformation du triangle en arbre (un peu longue), un petit algo récursif me donne ce résultat.
Bonne soirée
Clôture de l'énigme
La bonne réponse, comme presque tout l'a trouvée, est bien de 131.
Je regrette un peu d'avoir mis une pyramide peut-être trop petite, ou alors le choix des nombres à l'intérieur, car on pouvait visiblement trouver la solution "à vue d'oeil".
Sinon, en imaginant une pyramide plus grande, comment faire ?
L'examen brutal de tous les chemins possibles ne devient plus raisonnablement faisable à partir d'un certain nombre d'étages, même avec un programme.
Par contre, il existe une méthode toute simple, immédiate, et faisable avec un tableau.
Je vous renvoie vers les explications de castoriginal et LeDino, qui je crois sont les premiers à avoir évoqué cette méthode.
Nombre de participations : 0
Temps de réponse moyen : 106:03:18.