Inscription / Connexion Nouveau Sujet
Enigmo 253 : Nombre tri-penta-hexagonal
Bonjour tout le monde,
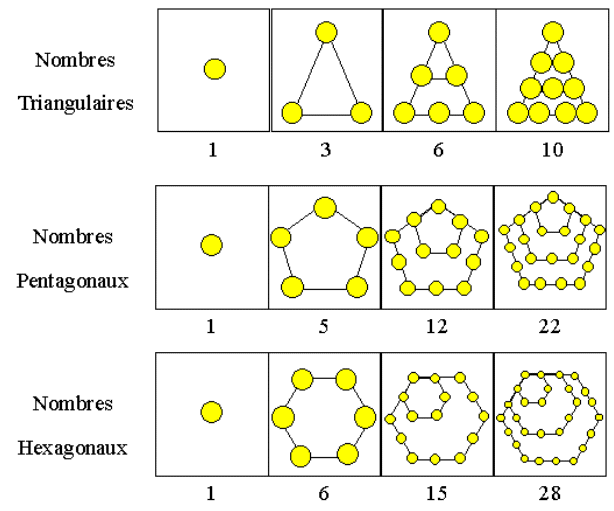
vous connaissez sans doute les nombres triangulaires, pentagonaux et hexagonaux. On les obtient à partir des figures ci-dessous.
Nombres triangulaires : T1=1 ; T2=3 ; T3=6 ; T4=10 ; T5=15 ; ...
Nombres pentagonaux : P1=1 ; P2=5 ; P3=12 ; P4=22 ; P5=35 ; ...
Nombres hexagonaux : H1=1 ; H2=6 ; H3=15 ; H4=28 ; H5=45 ; ...
Question : à part le nombre 1, trouver un nombre qui soit à la fois triangulaire, pentagonal et hexagonal.
Pour la réponse, je veux le nombre ainsi que son indice dans chacune des trois familles de nombres.
S'il en existe plusieurs, un seul suffira, et s'il n'en existe pas, alors vous répondrez "problème impossible".
Pour information, il existe des formules pour générer ces nombres, et attention de ne pas vous tromper, je sais par exemple qu'il existe aussi des nombres hexagonaux centrés qui ne sont pas les mêmes dont il est question ici.
Bonne recherche ! 
 Bonsoir à tous,
Bonsoir à tous,
j'ai personnellement trouvé
40755
les indices sont:
n3 pour les triangulaires = 285
n5 pour les pentagonaux = 167
n6 pour les hexagonaux = 145
Bien à vous
 Re bonjour,
Re bonjour,
Comme ces nombres sont extrèmement rares
Je donne hors classement  1 533 776 805
1 533 776 805
55 385 ° TRI
31 927 ° PENTA
27 693 ° HEXA
 Bonjour Jamo,
Bonjour Jamo,
Eh bien, on peut dire qu'il n'y en a pas des masses ! En dehors de 1, j'en ai trouvé trois en dessous de P10 000 000  0,15.1015 ; je te donne le troisième :
0,15.1015 ; je te donne le troisième :
(les choses se simplifient dès qu'on a vu que tout triangulaire de rang a impair est hexagonal de rang (a+1)/2, et réciproquement).
 Sauf erreur :
Sauf erreur :
T285 = P165 = H143 = 40 755
Merci pour l'énigme  .
.
Explication :
Tn - Tn-1 = n
Pn - Pn-1 = 3n - 2
Hn - Hn-1 = 4n - 3
Sur tableur, on construit les trois séries de proche en proche...
On peut ensuite trouver le nombre commun par des fonctions de recherche, ou par des tris...
 Bonjour Jamo.
Bonjour Jamo.
Je trouve le nombre 40755
avec 285 pour les triangulaires
493 pour les pentagonaux
et 569 pour les hexagonaux
Merci pour l'énigme
 Bonjour
Bonjour
De façon générale, on a toujours que . Mais trouver des nombres pentagonaux associés est moins simple.
Il semble que la plus petite combinaison soit:
J'avoue avoir été fainéant, et ne pas avoir cherché plus loin!
Merci pour l'Enigmo !
 Bonjour à tous,
Bonjour à tous,
Voici une réponse, je ne suis même pas certain que ce soit le plus petit :
40755
qui est le 285ème nombre triangulaire, le 165ème nombre pentagonal et le 143ème nombre hexagonal.
Merci pour cette jolie énigme,
Tof
 Bonjour,
Bonjour,
J'ai trouvé 40755 qui me semble être:
Triangulaire au rang 285
Pentagonal au rang 165
Hexagonal au rang 143
Encore une fois, c'est une moulinette basic qui m'a aidée. 
 Bonjour
Bonjour 
Alors je tente, j'ai fait mumuse avec mon tableur :
Je sais tout d'abord que tout nombre hexagonal est triangulaire dans un 1er temps.
Pour les nombres pentagonaux j'ai pris la formule : (3n² - n) /2
Pour les nombres hexagonaux : 2n² - n
J'ai rentré le nécessaire dans mon tableur, j'en trouve 1 (mais je n'ai pas cherché plus loin)
J'ai recherché les nombres hexagonaux centrés avec la formule : 3n² + n + 1 et je n'ai pas trouvé 40 755 parmi les nombres trouvés.
Ce qui fait, que j'en ai au moins un : 40 755
Des preuves :
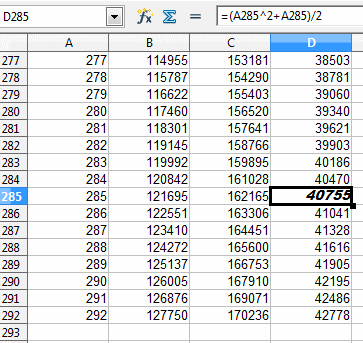
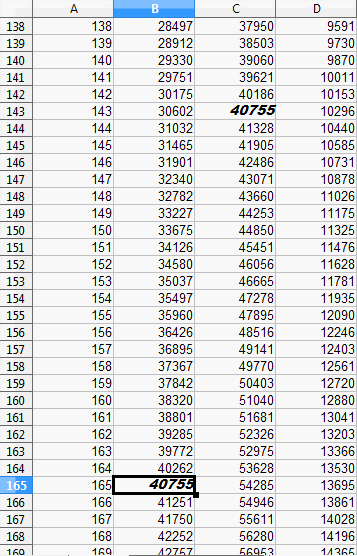
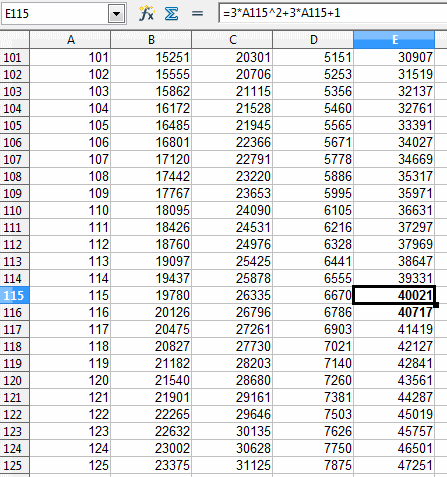
Voilà, je me suis peut-être trompée, mais au moins j'ai essayé cette énigme qui me branchait 
Ça me travaillait depuis hier soir.
Merci Jamo
 Bonjour,
Bonjour,
Par exemple: 40755
C'est le 285ème nombre triangulaire, le 165ème nombre pentagonal et le 143ème nombre hexagonal.
Merci pour l'énigme ! 
 Pour les nombres hexagonales, triangulaires et pentagonales,
Pour les nombres hexagonales, triangulaires et pentagonales,


 *.
*.
Donc 1 est le seul nombre à la fois hexagonal, pentagonal et triangulaire.
Donc problème impossible.
 Bonjour,
Bonjour,
avec les formules n(n+1)/2 , n(3n-1)/2 et n(2n-1) on peut assez facilement trouver (sans se soucier des triangulaires et en limitant la recherche par une réflexion sur la parité), le suivant de ces nombres.
Il s'agit de 40755 qui vérifie T285=P165=H143.
En revanche, après une recherche sur l'oeis on peut s'apercevoir que les suivants sont bien plus éloignés !
(1533776805, 57722156241751, 2172315626468283465, 81752926228785223683195, 3076689623521787481625080301, 115788137209866023854693048367775)
Merci pour l'enigmo.
 Re-salut,
Re-salut,
bon, ma réponse était fausse...
Mais pour la beauté du geste, je rectifie quand même:
40775 est le 143 ème nombre hexagonal, comme 40775=143*285,
, et c'est donc le 285è nombre triangulaire,
et c'est aussi le 165 ème nombre pentagonal, comme 40775=1/2*165*(3*165-1)
Merci pour l'énigme !
 Bonjour,
Bonjour,
40755 = T285 = P165 = H143.
Il est évidemment possible (et même très facile avec Excel) de générer les 3 listes et de les croiser.
Il doit néanmoins être possible de trouver une solution de façon logique. Bien que je n'y sois pas parvenu, voici une approche.
Soient Tn, Pn et Hn les nombres triangulaires, pentagonaux et hexagonaux de rang n.
Tn = n*(n+1)/2
Pn = n*(3n-1)/2
Hn = n*(2n-1)
Mais ce qui nous intéresse davantage sont les propriétés suivantes (qu'on vérifiera aisément avec les formules ci-dessus.
1) Hn = T2n-1; autrement dit les nombres hexagonaux sont les nombres triangulaires de rang impair.
On voit donc que l'énoncé qui semblait imposer 3 contraintes indépendantes revient à chercher un nombre qui soit à la fois pentagonal et triangulaire de rang impair.
2) Pn = T3n-1/3. (En regardant la formule de Tn, ilsaute aux yeux que les triangulaires de rang 3n et 3n-1 sont bien divisibles par 3).
Le problème revient donc à chercher un nombre triangulaire de rang de la forme 3n-1 dont le quotient par 3 soit lui-même un nombre triangulaire de rang impair.
Ainsi, il devient possible de résoudre le problème en se contentant de manipuler la liste des nombres triangulaires.
Il ne reste plus qu'à générer la liste, en examiner un élément sur 3 et voir si son quotient par 3 figure dans la liste.
Voici un petit programme Python qui fait cela (et qui ne se veut pas un exemple de programmation !)
#! /usr/bin/env python
# -*- coding:Utf8 -*-
def tester(nb):
"cherche si nb est un nombre triangulaire de rang impair"
ind = 1
while triang[ind] < nb:
ind = ind + 2
if triang[ind] == nb:
print('Nombre :', triang[ind], 'indice du triangulaire :', ind)
return
#
#Initialisation
n, element, triang = 1,0,[0]
while n < 601: #initialisation de la liste des 600 premiers nombres triangulaires
element = element + n
triang.append(element)
n = n + 1
# fin de l'initialisation
#
#on balaye les elements de la liste dont le rang est de la forme 3n-1.
n=5
while n < 600:
pent = triang[n]//3 # P(n)= 1/3 T(3n-1)
tester(pent)
n=n+3
print ('termine')
A l'exécution, on obtient immédiatement ceci :
Nombre : 40755 indice du triangulaire : 285
Merci pour l'énigme !
 Bonjour tout le monde
Bonjour tout le monde
Je propose: Problème impossible
Formule des nombres
-Triangulaires: (n²+n)/2 Eq.1
-Pentagonaux: (3n²-n)/2 Eq.2
-Hexagonaux: (4n²-2n)/2 Eq.3
Les égalités Eq.1= Eq.2 =Eq.3 donne pour seule valeur 1
 bonjour,
bonjour,
voici ma reponse : 40755
indice dans la suite des nombres triangulaires : 285
indice dans la suite des nombres pentagonaux : 165
indice dans la suite des nombres hexagonaux : 143
 Bonjour
Bonjour
Je propose le nombre 40755 qui est à la fois triangulaire (T285), pentagonal (P165) et hexagonal (H143)
Merci pour l'énigme. 
 Tout nombre triangulaire est de la forme t(t+1)/2 avec t entier > 0
Tout nombre triangulaire est de la forme t(t+1)/2 avec t entier > 0
Tout nombre pentagonal est de la forme p(3p - 1)/2 avec p entier >0
Tout nombre hexagonal est de la forme h(2h - 1) avec h entier >0.
On note que tout nombre hexagonal est nécessairement un nombre triangulaire.En effet, en posant h = (t+1)/2 avec t nombre entier impair, on obtient h(2h - 1) = t(t+1)/2
Dès lors pour résoudre le problème il suffit de trouver des entiers N qui sont en même temps pentagonaux et hexagonaux.
D'où l'équation diophantienne p(3p - 1) = 2h(2h - 1) qui s'écrit encore 4h² - 3p² - 2h + p = 0
Le site de Dario Alpern http://www.alpertron.com.ar/QUAD.HTM donne instantanément les solutions de cette équation qui sont définies par deux formules linéaires de récurrence dans laquelle h(i) et p(i)désignent la i-ème famille des nombres h et p tels que les nombres hexagonaux et pentagonaux correspondants sont égaux entre eux.
h(0) = 1
p(0) = 1
h(n+1) = A h(n) + B p(n) + K
p(n+1) = C h(n) + D p(n) + L
avec
A = 97 B = 84 K = -38
C = 112 D = 97 L = -44
A partir de la solution triviale h(0) = p(0) = 1, on déduit le deuxième couple h(1) = 143 et p(1) = 165 auquel correspond t(1) = 285.
Le nombre N qui est à la fois triangulaire, pentagonal et hexagonal vaut donc:
N = 285*286/2 = 165*494/2 = 143*285 = 40755
On peut poursuivre les calculs et on obtient:
h(2) = 27693 p(2) = 31977 t(2) = 55385 N = 1 533 776 805
h(3) = 5372251 p(3) = 6203341 t(3)= 10744501 N = 57 722 156 241 751
etc...
Si on ignore le site de Darion Alpern, on peut traiter l'équation du 2ème degré en h : 4h² - 2h - 3p² + p = 0 dont le discriminant est nécessairement un carré parfait.
On a alors 1 + 4(3p² - p) = q² ou encore l'équation diophantienne q² = 12p² - 4p - 1.Un tableur donne immédiatement la première solution non triviale avec p et q entiers l'un et l'autre : p = 165 et q = 571. L'obtention des autres solutions est évidemment un peu plus laborieuse.
 Il semble qu'il existe plusieurs nombres vérifiant cette condition on a par exemple :
Il semble qu'il existe plusieurs nombres vérifiant cette condition on a par exemple :
40 755
285 est son rang parmi les nombre triangulaires
165 est son rang parmi les nombre pentagonaux
143 est son rang parmi les nombre hexagonaux
1 533 776 805
55 385 est son rang parmi les nombre triangulaires
31 977 est son rang parmi les nombre pentagonaux
27 693 est son rang parmi les nombre hexagonaux
on prends 1 est le terme de rang 1(précision pour éviter les confusions)
Mathématiquement,
DARK_DUCK
 Problème impossible.
Problème impossible.
Ceux qui posent problème sont les nombres pentagonaux, qui n'ont rien à voir avec les deux autres.
Un nombre triangulaire d'ordre 2k-1 est un nombre hexagonal d'ordre k.
 Bonjour,
Bonjour,
Je propose 40755 qui est le 285ème nombre triangulaire, le 165ème nombre pentagonal et le 143ème nombre hexagonal.
Clôture de l'énigme
Le premier nombre était : T285=P165=H143=40755
Le suivant : T55385=P31977=H27693=1533776805
 Belle énigme
Belle énigme
Comme j'ai 2
J'en donnerais volontiers un à castoriginal car il
n'a que fourché de peu pour les rangs.
Nombre de participations : 0
Temps de réponse moyen : 109:37:20.

 à Louisa!
à Louisa!
