Inscription / Connexion Nouveau Sujet
Enigmo 270 : Les triangles Pythagodécimaux
Bonjour tout le monde,
nous allons nous intéresser dans cette énigme à une famille de triangles que j'ai décidé d'appeler "Pythagodécimaux".
Voici les caractéristiques d'un triangle Pythagodécimal :
- c'est un triangle rectangle dont les longueurs des côtés sont entiers ;
- l'hypoténuse est une puissance de 10 (10, 100, 1000, ...) ;
- les deux petits côtés ne sont pas des multiples de 10.
Voici deux exemples de tels triangles : (6;8;10) et (28;96;100).
En effet, on a bien :
Par contre, le triangle (60;80;100) ne convient pas à cause de la 3ème condition, les petits côtés ne doivent pas être des multiples de 10 (cette condition est là pour éviter de construire de nouveaux triangles à partir d'un autre en simplement multipliant les côtés par 10, 100, etc ...).
Pour l'énigme, je vous propose d'aller jusqu'au million ...
Question : Trouver tous les triangles Pythagodécimaux dont les hypoténuses sont égales à 10, 100, 1 000, 10 000, 100 000 et 1 000 000.
Donner les triangles sous la forme (a;b;c) où c est l'hypoténuse (comme en exemple).
On considérera que les triangles (a;b;c) et (b;a;c) sont les mêmes, inutiles de me les donner en double.
S'il existe d'autres triangles que ceux donnés en exemple dont l'hypoténuse est égale à 10 ou 100, je les veux aussi.
Et si ça se trouve, il n'existe pas d'autres triangles que les deux donnés exemple !
Bonne recherche ! 

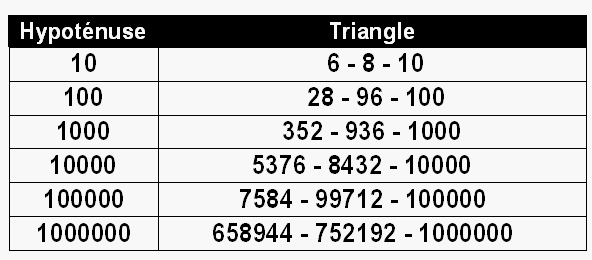
 Avec l'hypothénuse 10, il y a 1 triangle
Avec l'hypothénuse 10, il y a 1 triangle
[6, 8, 10]
Avec l'hypothénuse 100, il y a 1 triangle
[28, 96, 100]
Avec l'hypothénuse 1000, il y a 1 triangle
[352, 936, 1000]
Avec l'hypothénuse 10000, il y a 1 triangle
[5376, 8432, 10000]
Avec l'hypothénuse 100000, il y a 1 triangle
[7584, 99712, 100000]
Avec l'hypothénuse 1000000, il y a 1 triangle
[658944, 752192, 1000000]
 Salut jamo,
Salut jamo,
Je propose les triangles suivants :
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
 J'en ai 6.
J'en ai 6.
(6;8;10)
(28;96;100)
(352;936;1 000)
(5 376;8 432;10 000)
(7 584;99 712;100 000)
(658 944;752 192;1 000 000)
Voilà.
C'était marrant, merci. 
 Bonjour,
Bonjour,
Je propose :
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
 Salut, Jamo, et merci pour l'enigme.
Salut, Jamo, et merci pour l'enigme.
Je propose les triangles suivants:
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
Je croise les doigts pour qu'il n'y en ait pas d'autres...
 Bonjour Jamo
Bonjour Jamo  merci pour l'enigmo
merci pour l'enigmo
10 : (8;6;10)
100 : (28. 96. 100)
1000: (352. 936. 1000)
10'000 : (5376. 8432. 10000)
100'000 : (7584. 99712. 100000)
1'000'000 : (658944. 752192. 1000000)
Voici mon programme sous Scilab ( moins de 2.57 s pour trouver pour 10^6 )
Comme on avait C fixé, mon idée a été d'avoir qu'une seule variable A et apres d'en déduire B, on évite comme ça les deux boucles for et donc du temps, de plus j'ai remarqué que la premiere variable était toujours divisible par 4 :
tic()
C=1000000
for A=0:4:10^6
if A^2>C^2 then
break;
end
B=sqrt(C^2-A^2)
if int(B)==B & modulo(A,10)<>0 & modulo(B,10)<>0 then
disp(C,B,A)
end
end
disp(toc())
 Bonjour,
Bonjour,
j'ai toujours fait mes enigmes à la main ou presque (feuille calcul excel) mais la clairement il faut faire un algorithme!
Je me suis donc lancé avec Algobox et ai un peu galéré pour comprendre que = c'est == et que afficher n affiche n et pas sa valeur...
Au final 15, 20 lignes pour trouver les solutions suivantes:
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
Les solutions ont été trouvées en quelques secondes par la machine: en fait c'est un peu décevant comme brain teaser...
J'attend avec impatience la suivante...
A bientot
 Bonjour Jamo,
Bonjour Jamo,
Il n'y en a qu'un à chaque fois :
(6 ; 8 ; 10) (28 ; 96 ; 100) (352 ; 936 ; 1000) (5376 ; 8432 ; 10000) (7584 ; 99712 ; 100000) (658944 ; 752192 ; 1000000)
 Bonsoir,
Bonsoir,
Il semble qu'il y ait un triplet solution pour chaque puissance de 10 :
( 6 ; 8 ; 10 )
( 28 ; 96 ; 100 )
( 352 ; 936 ; 1.000 )
( 5.376 ; 8.432 ; 10.000 )
( 7.584 ; 99.712 ; 100.000 )
( 658.944 ; 752.192 ; 1.000.000 )
Merci pour l'énigme  !
!
 ( 6 ; 8 ; 10 )
( 6 ; 8 ; 10 )
( 28 ; 96 ; 100 )
( 352 ; 936 ; 1000 )
( 5376 ; 8432 ; 10000 )
( 7584 ; 99712 ; 100000 )
( 658944 ; 752192 ; 1000000 )
Merci pour l'énigme
XCAS :
Pytd(n):={
local c , j , p , x , y , r ;
r:=1;
pour j de 1 jusque n faire
r:=r*10;
y:= floor(r/sqrt(2))+1;
p:=1;
pour x de floor(r/sqrt(2)) jusque r faire
c:=0;
while (x*x + y*y > r*r) {y:=y-1 ;if (c==1){p:=p+1}; c:=c+1}
if ((x*x + y*y == r*r) et (x/10<>floor(x/10)) et (y/10<>floor(y/10))) { afficher(y,x,r);}
y:=y-p;
fpour;
fpour;}:;
 Bonjour Jamo,
Bonjour Jamo,
Sauf erreur(s), et en recopiant les exemples donnés:
(6 ,8 ,10 )
(28 ,96 ,100 )
(352 ,936 ,1000)
(5376 ,8432 ,10000)
(7584 ,99712 ,100000)
(658944,752192,1000000)
Merci pour l'énigmo.
 Bonjour tout le monde !
Bonjour tout le monde !
Chose amusante, je n'en trouve qu'un par puissance de 10 :
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
Merci pour l'énigme
 Bonjour
Bonjour
Je dirais
(6, 8, 10 ) : le premier exemple
(28, 96, 100 ) : le deuxième exemple
(352, 936, 1000 )
(5376, 8432, 10000 )
(7584 , 99712, 100000 )
(658944,752192, 1000000 )
Merci
A+
 Bonjour,
Bonjour,
Je propose:
les deux de l'exemple
10 6 8
100 28 96
avec
1000 352 936
10 000 5376 8432
100 000 7584 99712
1 000 000 658944 752192
 Bonjour à tous,
Bonjour à tous,
Je propose les triplets suivants :
(6,8,10)
(28,96,100)
(352,936,1000)
(5376,8432,10000)
(7584,99712,100000)
(752192,659944,1000000)
Et j'espère ne pas en avoir oublié, je ne suis pas certain cette fois-ci.
Merci pour l'énigme,
Tof
 Bonjour,
Bonjour,
Voici ma réponse :
Je trouve au total 6 triangles Pythagodécimaux, un pour chaque hypoténuse.
(6, 8, 10)
(28, 96, 100)
(352, 936, 1000)
(5376, 8432, 10000)
(7584, 99712, 100000)
(658944, 752192, 1000000)
Merci!
 Bonjour.
Bonjour.
Ma réponse :
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
Cordialement
 Bonjour,
Bonjour,
Stabilité de formes quadratiques:
Tous ces nombres sont des entiers positifs.
Ici, cas particulier:
Alain
 Bonjour,
Bonjour,
Je trouve 1 triangle par hypothénuse
(6; 8; 10)
(28; 96; 100)
(352; 936; 1000)
(5376; 8432; 10000)
(7584; 99712; 100000)
(658944; 752192; 1000000)
10^2 = 6^2 + 8^2
100^2 = 28^2 + 96^2
1000^2 = 352^2 + 936^2
10000^2 = 5376^2 + 8432^2
100000^2 = 7584^2 + 99712^2
1000000^2 = 658944^2 + 752192^2
 Bonjour,
Bonjour,
Encore une fois, le Quick Basic m'a aidé. Mais j'ai des doutes sur ma programmation.
Je trouve qu'un triangle pour chaque valeur de l'hypoténuse. Ce qui donne:
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
 Bonjour
Bonjour
voici la reponse que je propose:
il y a un triangle pythagodécimal pour chaque puissance de 10 donnée (à une permutation près entre les petits cotés !), à savoir:
(6; 8; 10)
(28; 96; 100)
(936; 352; 1000)
(8432; 5376; 10000)
(7584; 99712; 100000)
(752192; 658944; 1000000)
merci pour l'enigme
pour trouver ces triangle, il faut rechercher les couple (x;y) tels que x2 + y2 = 5n en incrémentant n à chaque étape et en utilisant que 5 = 22 + 12 (n=1)
 Salut :
Salut :
*pour 10 :
(6,8,10)
*pour 100:
(28,96,100)
*pour 1000:
(352,936,1000)
*pour 10 000:
(5376,8432,10000)
*pour 100 000:
(2432,37472,100000)
(7584,99712,100000)
(15488,34208,100000)
 Bonjour.
Bonjour.
(6; 8; 10)
(28; 96; 100)
(352; 936; 1000)
(5376; 8432; 10000)
(7584; 99712; 100000)
(658944; 752192; 1000000)
Quand le pgcd du triplet est 1, le plus grand nombre est impair. En l'occurrence, c'est la puissance de 5 la plus grande possible, car autrement, le multiplicateur pour revenir à une puissance de 10 serait divisible par 10.
programme de la macro Visual Basic :
Sub pythagore()
Dim hyp As Long, a As Long, c As Double
hyp = Application.InputBox(prompt:="hypoténuse")
For a = 1 To Int(hyp / Sqr(2))
c = Sqr(hyp ^ 2 - a ^ 2)
If c = Int(c) Then
MsgBox (c & " " & a)
End If
Next a
End Sub
on entre successivement 5, 25, 125, 625, 3125 et 15625 et on multiplie les résultats respectivement par 2, 4, 8, 16, 32 et 64, en omettant les multiples de 5.
 Bonjour jamo,
Bonjour jamo,
Ma solution:
(6; 8; 10)
(28; 96; 100)
(352; 936; 1 000)
(5 376; 8 432; 10 000)
(7 584; 99 712; 100 000)
(658 944; 752 192; 1 000 000)
Et pour le plaisir:
(2 063 872; 9 784 704; 10 000 000)
(42 197 248; 90 660 864; 100 000 000)
(472 103 424; 881 543 168; 1000 000 000)
Merci pour l'énigme ! 
 Bonjour,
Bonjour,
Je trouve un nouveau triangle pour chaque ordre de grandeur :
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
(658944;752192;1000000)
Merci pour l'enigmo !
 Bonjour
Bonjour  ,
,
Je propose:
6²+8²=10²
28²+96²=100²
352²+936²=1000²
5376²+8432²=10000²
7584²+99712²=100000²
658944²+752192²=1000000²
Pour chaque puissance de 10 la solution est unique.
Programme utilisé:
> Pythagodecimaux := proc(n)
local a,b;
for a from 1 to floor((10^n-1)/(sqrt(2))) do
if a mod 10<>0 and frac(evalf(sqrt(100^n-a^2),12))=0 then print(a,sqrt(100^n-a^2),10^n);
fi: od: end;
 Bonjour tout le monde
Bonjour tout le monde
- Je propose ceci:
(6, 8, 10)
(28, 96, 100)
(352, 936, 1000)
(5376, 8432, 10000)
(7584, 99712, 100000)
(658944, 752192, 1000000)
 Bonjour
Bonjour
6 solutions
10 6 8
100 28 96
déja données
----
1000 352 936
10000 5376 8432
100000 7584 99712
1000000 658944 752192
 Bonjour et merci pour l'énigme !
Bonjour et merci pour l'énigme !
Je vais répondre tout en étant très peu certain de ne pas avoir oublié de configurations possibles. Je me suis aidé d'un programme et lorsque l'hypoténuse vaut 1 million c'est trop... Donc voilà, il est très peu probable que je reçoive le smiley mais sait-on jamais !  Donc voici mes propositions :
Donc voici mes propositions :
(6;8;10)
(28;96;100)
(352;936;1000)
(5376;8432;10000)
(7584;99712;100000)
À bientôt 
Clôture de l'énigme
Pour cette article, je me suis inspiré d'un article paru dans un bulletin de l'APMEP, où on cherchait les angles tels que leurs cosinus et sinus soient des nombres décimaux, c'est-à-dire les couples de décimaux (x;y) tels que x²+y²=1.
Ce problème est bien entendu équivalent au problème que je proposais ici.
Dans cet article, il était démontré qu'il existe un seul triangle par "décade". De plus, il me semble bien qu'ils y donnaient des formules permettant de tous les calculer (des formules par récurrence je crois bien).
Enfin bref, bravo à tous ceux qui ont trouvé les solutions !
 Bonjour,
Bonjour,
Pour moi les solutions peuvent se construire
à fur et à mesure à partir des relations connues:
Sur les deux , une convient,
Alain
Nombre de participations : 0
Temps de réponse moyen : 88:30:34.