Inscription / Connexion Nouveau Sujet
Enigmo 280 : La règle incomplète
Bonjour tout le monde,
tout professeur de mathématiques est souvent exaspéré par l'état du matériel de ses élèves, ne serait-ce que pour une simple règle : les règles sont cassées en morceaux, les graduations sont effacées, ...
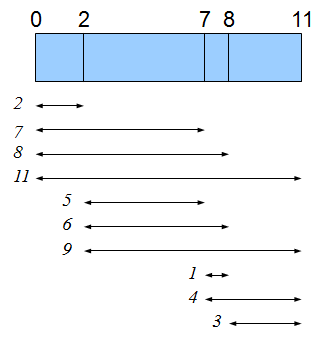
La dernière fois, je suis tombé sur un élève qui avait une règle de 11 cm, de 0 à 11, où il ne restait que les graduations 2, 7 et 8.
Je me suis alors aperçu qu'en prenant tous les écarts entre 2 graduations (y compris le 0 et le 11), on ne trouvait jamais la même valeur !
La figure ci-dessous en donne une illustration.
(d'ailleurs, on remarquera qu'on aurait presque pu avoir toutes les valeurs entre 1 et 11, il ne manque que le 10)
Le voisin de cet élève, qui avait une règle de 25 cm, de 0 à 25, et 5 graduations encore visibles entre les extrémités, présentait exactement la même particularité : tous les écarts entre 2 graduations quelconques étaient différents !
Question : donner les 5 graduations encore visibles sur la règle de 25 cm pour que tous les écarts entre 2 graduations soient différents.
Quelques petites précisions :
- il y a en tout 7 graduations : le 0, le 25, et les 5 autres entre ces deux extrémités ;
- les valeurs des 5 graduations demandées sont entières ;
- vous donnerez la réponse sous la forme : 0 ? ? ? ? ? 25 ;
- inutile de me donner la liste de tous les écarts ;
- s'il existe plusieurs solutions, une seule me suffira ;
- s'il n'existe pas de solutions, alors vous répondrez "problème impossible".
Voilà, je pense ne rien avoir oublié.
Je pense que le principe de l'énigme est assez simple, mais j'ai tout de même décidé de mettre 3 étoiles pour la difficulté, il se pourrait que la recherche d'une éventuelle solution ne soit pas aisée (mais je me trompe peut-être).
Bonne recherche ! 
 Salut Jamo, salut Nofutur!
Salut Jamo, salut Nofutur!
Je trouve la configuration ci-dessous:
0-2-3-10-16-21-25.
J'ai pas vérifié son unicité, mais elle marche si je ne me trompe. Merci beaucoup, celle-ci était très agréable...
 Bonjour à tous,
Bonjour à tous,
Je trouve pas mal de solutions. L'une d'entre elles :
0 / 1 / 4 / 10 / 18 / 23 / 25
Juste une question : Comment faites-vous pour trouver toutes ces idées d'énigmes ? J'en écris moi-même de temps en temps, mais je n'ai pas votre productivité ni votre originalité !
Merci
 Bonjour,
Bonjour,
Voici 5 graduations encore visibles sur la règle de 25 cm pour que tous les écarts entre 2 graduations soient différents :
[0, 1, 4, 10, 18, 23, 25]
Merci pour cette énigme !
 Bonjour,
Bonjour,
voici une solution en image:
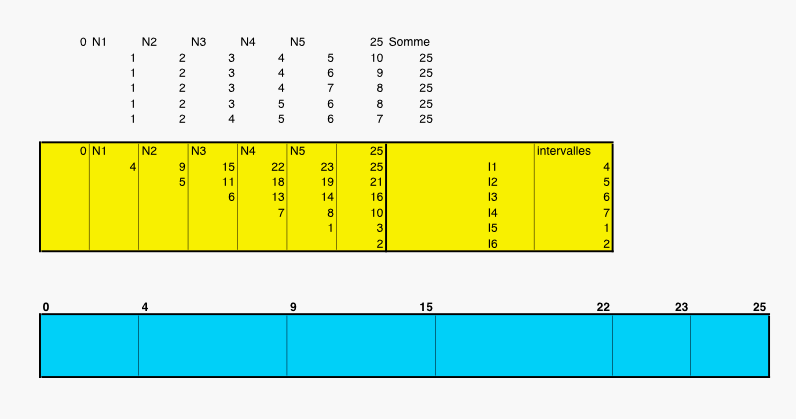
Les premières lignes du tableau représentent les seules possibilités de distribution des intervalles puisque leur somme doit être de 25.
Le cadre jaune montre tous les intervalles différents correspondant à la ligne 5.
Le cadre bleu représente la réglette avec ses dernières graduations
Bien à vous
 Bonjour,
Bonjour,
Voici ma réponse :
1, 2, 3, 5, 9, 14, 25
Sauf erreur de compréhension de l'énoncé de ma part il semblerait qu'il y ait pas mal de solutions !
 Oui il y a bien erreur de ma part (et c'est seulement après avoir poster que je m'en rend compte
Oui il y a bien erreur de ma part (et c'est seulement après avoir poster que je m'en rend compte  )
)
Je n'ai pas tenu compte des nombres 1 et 25 dans ma recherche (seulement des cinq nombres du milieu). Voilà !

 Bonjour,
Bonjour,
Je pense qu'il est impossible e trouver des mesures
sans doublon:
En effet il faudrait trouver 6+5+4+3++1 =21 mesures
différentes en ayant par ailleurs à exclure les nombres
doubles ou moitié exemple 4 exclut 2 et 9 exclut 18
comme il y aura au moins 6 exclusions donc 26-6 =20
possibilités <21
 Après réflexion et donc poisson:
Après réflexion et donc poisson:
Il y a seulement 4 exclusions
donc 21 intervalles avec
4 9 15 22 23 25
 Bonjour,
Bonjour,
Je trouve
0, 1, 11, 16, 19, 23, 25
Démarche :
Il y a 5 graduations, donc 6 intervalles. Le plus grand intervalle possible est 10 et les intervalles ont ces 4 configurations possibles.
1 2 3 4 5 10
1 2 3 4 6 9
1 2 3 4 7 8
1 2 3 5 6 8
J'ai pris la première et grâce à quelques considération simples (1 ne peut pas être collé à 2, 3 ou 4 par exemple) et quelques essais, je suis arrivé à
1 10 5 3 4 2
Merci pour l'énigme. 
 0,1,4,10,18,23,25
0,1,4,10,18,23,25
Merci Jamo
Et bonjour à tous
Je trouve 10 réponses ( ou 5 avec la symétrie)
[[0,1,4,10,18,23,25],[0,1,7,11,20,23,25],[0,1,11,16,19,23,25],[0,2,3,10,16,21,25],[0,2,5,14,18,24,25],[0,2,6,9,14,24,25],[0,2,7,13,21,22,25],[0,2,7,15,21,24,25],[0,3,4,12,18,23,25],[0,4,9,15,22,23,25]]
 Bonjour!
Bonjour!
Je trouve comme solutions :
0 1 4 10 18 23 25
0 1 7 11 20 23 25
0 1 11 16 19 23 25
0 2 3 10 16 21 25
0 2 5 14 18 24 25
0 2 6 9 14 24 25
0 2 7 13 21 22 25
0 2 7 15 21 24 25
0 3 4 12 18 23 25
0 4 9 15 22 23 25
 Un solution serait : 0 1 4 10 18 23 25
Un solution serait : 0 1 4 10 18 23 25
Toutes les solutions avec les écarts :
Graduations : 0 1 4 10 18 23 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 21, 22, 23, 24, 25]
Graduations : 0 1 7 11 20 23 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 16, 18, 19, 20, 22, 23, 24, 25]
Graduations : 0 1 11 16 19 23 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 16, 18, 19, 22, 23, 24, 25]
Graduations : 0 2 3 10 16 21 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16, 18, 19, 21, 22, 23, 25]
Graduations : 0 2 5 14 18 24 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, 16, 18, 19, 20, 22, 23, 24, 25]
Graduations : 0 2 6 9 14 24 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 14, 15, 16, 18, 19, 22, 23, 24, 25]
Graduations : 0 2 7 13 21 22 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 18, 19, 20, 21, 22, 23, 25]
Graduations : 0 2 7 15 21 24 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 13, 14, 15, 17, 18, 19, 21, 22, 23, 24, 25]
Graduations : 0 3 4 12 18 23 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, 15, 18, 19, 20, 21, 22, 23, 25]
Graduations : 0 4 9 15 22 23 25
Ecarts : [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 13, 14, 15, 16, 18, 19, 21, 22, 23, 25]
A+
Torio
 Bonjour et mille mercis Jamo pour ce nouvel enigmo,
Bonjour et mille mercis Jamo pour ce nouvel enigmo,
Je trouve dix solutions. (Encore une fois, avec Quick Basic)
En voici une: 0 1 4 10 18 23 25
Au format demandé. 
 Bonjour
Bonjour
Voici une solution au problème posé :
0 1 4 10 18 23 25
Il en existe plusieurs autres, dont
0 1 7 11 20 23 25
0 1 11 16 19 23 25
0 2 3 10 16 21 25
0 2 5 14 18 24 25
0 2 6 9 14 24 25
0 2 7 13 21 22 25
0 2 7 15 21 24 25
0 3 4 12 18 23 25
0 4 9 15 22 23 25
Merci pour l'énigmo !
 Bonjour,
Bonjour,
histoire de répondre (en trichant, Google, Wikipedia)
il s'agit des règles de Golomb
par exemple
0 2 7 13 21 22 25
________
il y a 5 solutions avec une règle de taille 25 à 7 graduations en tout
Le problème des règles à 27 graduations, de longueur minimale, n'est pas résolu. (c'est actuellement un problème ouvert, qui nécessite une puisance de calcul phénoménale)
Ce problème répond aussi à la question ludique :
je dispose de 7 sacs de 25 pièces de 10g chacune, un d'eux contient des pièces toutes fausses plus légères de 1g, et un autre contient des pièces toutes fausses plus lourdes de 1g.
En une seule pesée déterminer quels sont les sacs de pièces fausses.
 Bonjour Jamo.
Bonjour Jamo.
0 1 11 16 19 23 25
1 : 0-1
2 : 23-25
3 : 16-19
4 : 19-23
5 : 11-16
6 : 19-25
7 : 16-23
8 : 11-19
9 : 16-25
10 : 1-11
11 : 0-11
12 : 11-23
13 : manque
14 : 11-25
15 : 1-16
16 : 0-16
17 : manque
18 : 1-19
19 : 0-19
20 : manque
21 : manque
22 : 1-23
23 : 0-23
24 : 1-25
25 : 0-25
vingt et une distances différentes.
 Bonjour Jamo,
Bonjour Jamo,
Je trouve 10 solutions, en comptant les solutions symétriques par rapport au milieu de la règle.
L'une d'entre elles est : 0 - 4 - 9 - 15 - 22 - 23 - 25
Et merci.
 10 solutions dont (0,2,3,10,16,21,25) qui conduit à la plus petite moyenne des nombres gradués.
10 solutions dont (0,2,3,10,16,21,25) qui conduit à la plus petite moyenne des nombres gradués.
Merci pour l'énigme
 Il y a plusieurs réponses
Il y a plusieurs réponses
en voici une
0, 4, 9, 15, 22, 23, 25
une autre
0,1,7,11,20,23,25
on aurait pu y ajouter un critère du genre faites que la somme des nombres soit minimum pour limiter le nombre de réponses. Je n'ai pas poussé le PC à tout calculer
Fait avec Excel et 'what-if' analyse
Merci pour cette enigme
 0 1 7 11 20 23 25
0 1 7 11 20 23 25
0 2 5 14 18 24 25
0 2 7 13 21 22 25
0 3 4 12 18 23 25
Bon courage pour vérifier... 
 Bonjour,
Bonjour,
Voici une solution : 0 1 4 10 18 23 25
J'ai compté en tout 10 solutions (ou 5 si on ne tient pas compte des symétriques).
Clôture de l'énigme
Ce problème est inspiré de ce qu'on appelle les règles de Colomb : ![]()
Il en existe 10 différentes avec 7 graduations (en fait 5 uniques si on élimine les symétries).
Les règles de Colomb sont aussi liées aux suites de Sidon (ou ensembles de Sidon) : ![]() (on ne trouve pas grand chose en français là-dessus).
(on ne trouve pas grand chose en français là-dessus).
Nombre de participations : 0
Temps de réponse moyen : 81:04:55.


