Inscription / Connexion Nouveau Sujet
Enigmo 290 : Un problème d'intersection
Bonjour tout le monde,
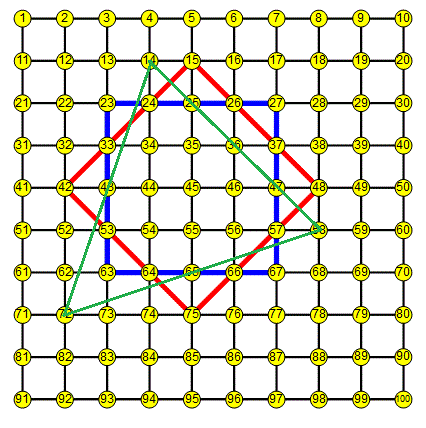
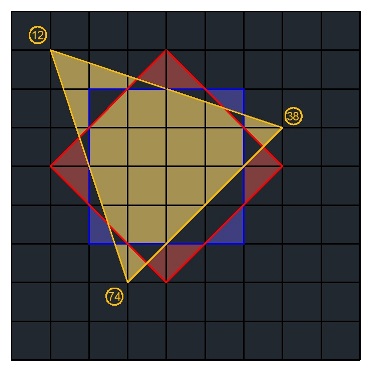
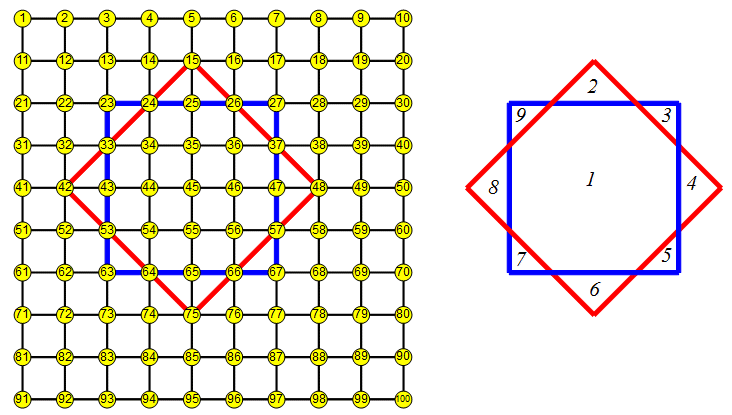
j'ai tracé ci-dessous deux carrés (un rouge et un bleu) qui se croisent et définissent ainsi 9 zones (on appelle une "zone" un polygone non-croisé).
Je souhaite maintenant rajouter à la figure un triangle à placer de telle sorte à obtenir le maximum de zones.
Par contre, surtout pour faciliter le moyen de donner la réponse et la correction, les sommets du triangle ne peuvent être situés que sur les 100 cases numérotées.
Quelques remarques et précisions :
- le triangle peut être quelconque ;
- les sommets du triangle doivent obligatoirement être sur les 100 cases définies, même si on pourrait faire mieux en les plaçant ailleurs ;
- les sommets du triangle peuvent être sur les sommets des carrés ;
- les cases numérotées doivent être considérés comme des points ;
- l'épaisseur des traits a bien entendu été exagéré sur la figure ci-dessous, les côtés des polygones sont des segments.
Question : Quel est le nombre maximal de zones qu'on peut obtenir en ajoutant un triangle aux deux carrés, et comment placer ce triangle ?
Pour la réponse, vous me donnerez tout d'abord le nombre total de zones obtenu, puis les cases des 3 sommets du triangle.
Bonne recherche ! 
 bonjour
bonjour
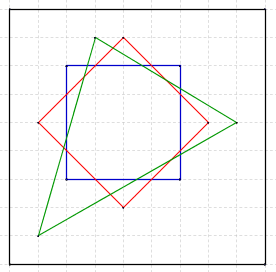
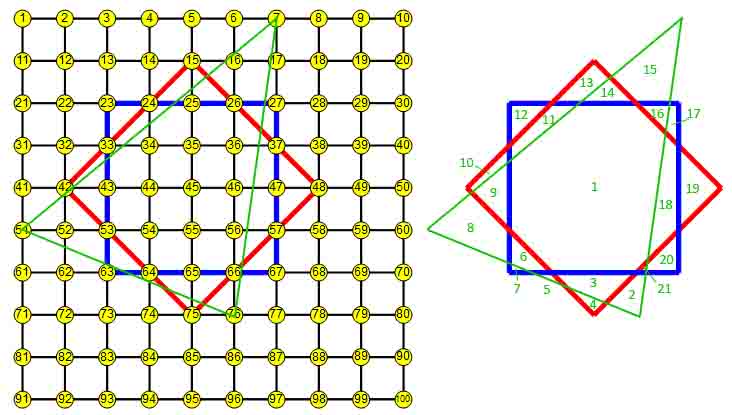
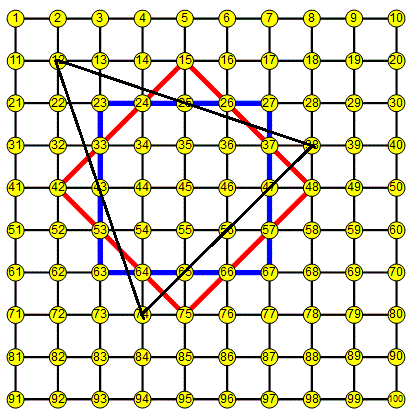
je trouve 21 zones avec le triangle dont les sommets sont placés en (7,54,76).
(voir illustration ci-dessous)
... en espérant bien sûr être encore capable de compter correctement, ce qui est loin d'être sûr un lundi matin 
Merci pour l'énigmo et à bientôt !
 Je pense que l'on ne peut pas ajouter plus de 12 zones aux 9 zones existantes...En fait toute droite ne peut couper les 8 côtés qu'en 4 points au maximum..
Je pense que l'on ne peut pas ajouter plus de 12 zones aux 9 zones existantes...En fait toute droite ne peut couper les 8 côtés qu'en 4 points au maximum..
Le nombre maximal de zones que l'on peut atteindre est donc 21..
Les somments peuvent être par exemple en 18,32 et 85. L'important est de ne jamais passer par une intersection existante.
Tout celà sans aucune certitude ...
 Bonjour
Bonjour
En épèrant que les traits ne soient pas trop épais...
Je trouve 21 zones
Mon triangle à ses sommets en 14 39 81
 Bonjour,
Bonjour,
Le nombre maximal de zones qu'on peut obtenir en ajoutant un triangle aux deux carrés est 21.
Il suffit de prendre le triangle de sommets 1, 38, 74.
Merci pour cette énigme !
 Bonjour à tous,
Bonjour à tous,
J'ai beau chercher, je ne trouve pas mieux que 21 zones.
Voici un placement possible du triangle : 13 - 38 - 86
Merci pour l'énigme
 Bonjour Jamo,
Bonjour Jamo,
Comme une droite ne peut pas subdiviser plus de 3 zones existantes, on arrive au maximum à 12 zones supplémentaires en comptant les trois "pointes" du triangle.
Je réponds donc qu'on peut arriver au total à : 21 zones maximum
Et on peut y arriver avec un tas de triangles différents, et notamment : le triangle 12 - 38 - 74
qui respecte la symétrie du problème :
 Pour chaque côté du triangle, au maximum 4 points d'intersection. Ceci en fait 12, découpant 12 nouvelles frontières sur le bord du triangle : on ne peut pas espérer plus de 21 zones.
Pour chaque côté du triangle, au maximum 4 points d'intersection. Ceci en fait 12, découpant 12 nouvelles frontières sur le bord du triangle : on ne peut pas espérer plus de 21 zones.
On arrive bien à 21 zones en prenant les sommets du triangle en 32 - 18 - 76.
 Bonjour à tous,
Bonjour à tous,
Merci à Jamo pour ce problème.
21 zones définies par le triangle de sommets 12,38,74.
Pas de méthode spéciale pour trouver, obtenue par analyse brutale des 970200 les triangles.
 Bonsoir,
Bonsoir,
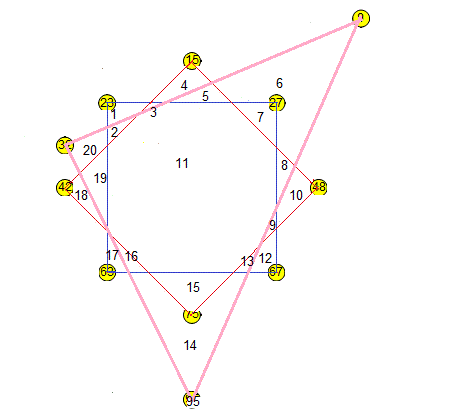
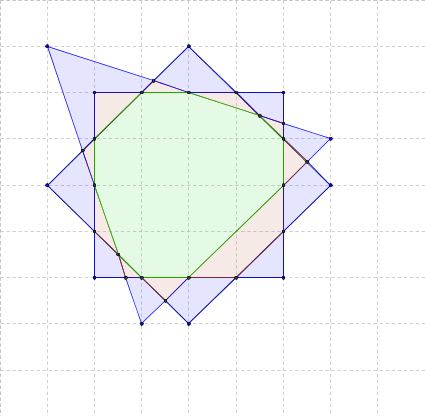
en divisant les 8 zones autour du centre (de 2 à 9) en deux, celle du centre en trois parties supplémentaires et en en créant trois à l'extérieur, on atteint un maximum théorique de 23 zones ( 8×2 + 1×4 + 3 ).
En revanche je pense que les zones comprises entre les deux carrés ne peuvent toutes être simultanément divisées en deux.
J'en arrive à un maximum de 21 avec l'image ci-dessous et le triplet (2;49;74).
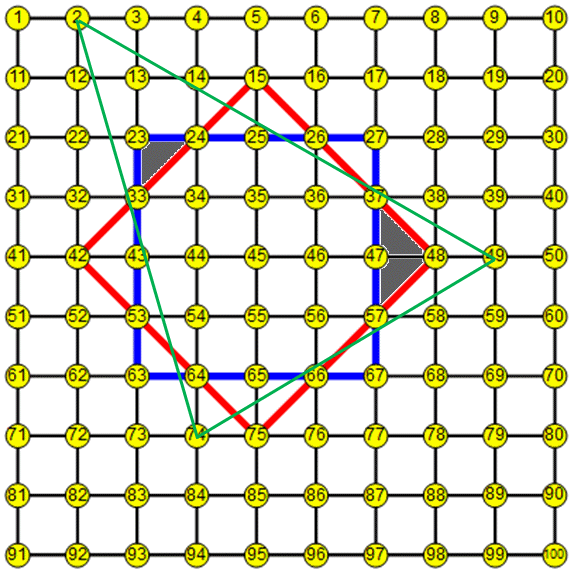
(Les zones grises sont les deux qui n'ont pas été partagées)
NB: Les solutions à 21 sont légions !
Merci jamo pour l'enigmo sur laquelle on ne se précipite pas... 22 ? Nooon !
( et bon courage pour la correction ! Pas facile ! )
 Merci à Jamo pour cette énigme.
Merci à Jamo pour cette énigme.
Le dessin fourni, qui contient 9 zones, donne à penser que les zones n'ont deux à deux aucun point commun autre que ceux de leur bordure commune.
Je remarque aussi que l'énoncé élimine les polygones croisés mais pas les polygones non convexes.
J'obtiens ainsi 21 zones en plaçant les sommets du triangle sur les cases
16,52,78.
 Bonjour Jamo,
Bonjour Jamo,
Dur,dur!
21 zones avec les points: 1-38-47.
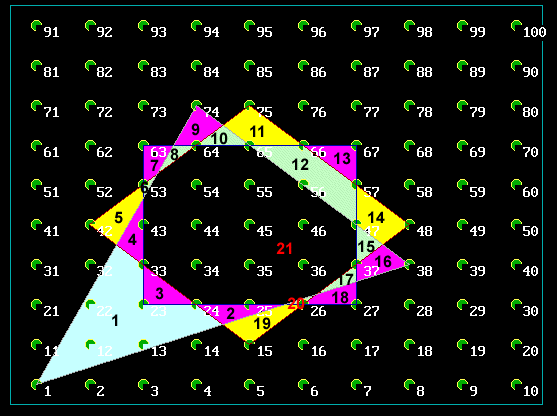
Merci pour la recherche et la programmation.
 Salut jamo,
Salut jamo,
je trouve un maximum de 21 en plaçant les trois sommets du triangle aux points 1, 39 et 74.
Merci.
 Nombre total de zones = 21
Nombre total de zones = 21
Les 3 sommets : 22 - 39 - 74
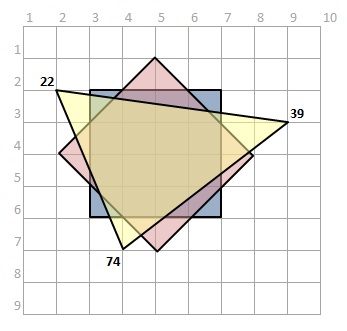
Explication :
On a 9 zones au départ.
Chaque nouvelle intersection de segments rajoute une zone.
Chaque segment peut couper chaque carré 2 fois au plus... car les carrés sont convexes.
Donc en tout les 3 cotés du triangle peuvent couper au plus 3*2*2 = 12 segments.
On peut donc ajouter au plus 12 zones aux 9 de départ.
21 zones est donc le maximum atteignable.
Il suffit donc de trouver un triangle parmi les nombreux qui conviennent.
 Bonsoir,
Bonsoir,
je trouve un maximum de 21 zones en plaçant les sommets du triangle sur les cases 16 - 52 - 78.
Merci pour l'énigme,
Dagon
 Bonjour,
Bonjour,
je trouve 20 cases (enfin je crois...) avec un triangle dont les sommets sont en 52, 16 et 78.
A bientôt et merci!
 c'est moche.... j'avais bien intégré les trois intersections max par coté du triangle, j'ai le bon triangle... mais j'ai du oublier de compter la zone centrale.....
c'est moche.... j'avais bien intégré les trois intersections max par coté du triangle, j'ai le bon triangle... mais j'ai du oublier de compter la zone centrale.....
D'un autre côté on a que 20 doigts en comptant sur les mains et les pieds alors je ne pouvais pas trouver 21
Enfin! je renoue avec mes poissons stupides pas 
 J'aurais une petite question pour les poseurs d'énigme aussi bien que pour les posteurs.
J'aurais une petite question pour les poseurs d'énigme aussi bien que pour les posteurs.
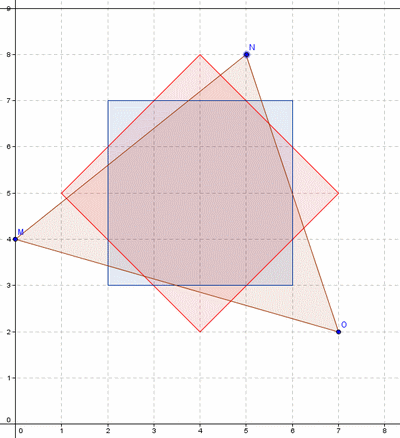
Quel(s) logiciel(s) utilisez-vous pour faire vos dessins ? J'ai fait quelque tentatives avec paint mais c'était un vrai désastre.
 Comme Torio et Pdiophante probablement, j'utilise "Geogebra" qui est gratuit, relativement facile d'utilisation et donne d'assez jolis dessins.
Comme Torio et Pdiophante probablement, j'utilise "Geogebra" qui est gratuit, relativement facile d'utilisation et donne d'assez jolis dessins.
Tape Geogebra sur ton moteur de recherches ...
Je fais mes dessins avec le logiciel "Draw" de la suite OpenOffice.
Il permet de tracer toutes sortes de choses avec précision, d'inclure des images pour faire des montages, ...
Nombre de participations : 0
Temps de réponse moyen : 95:38:37.