Inscription / Connexion Nouveau Sujet
Enigmo 302 : Un triangle différent
Bonjour tout le monde,
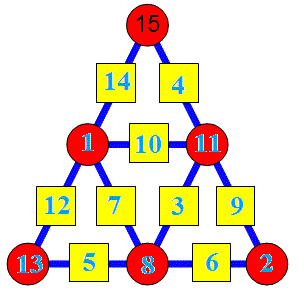
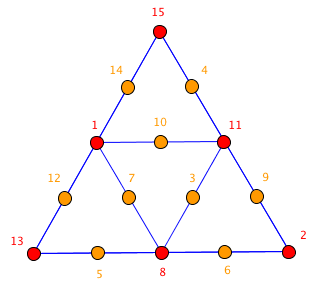
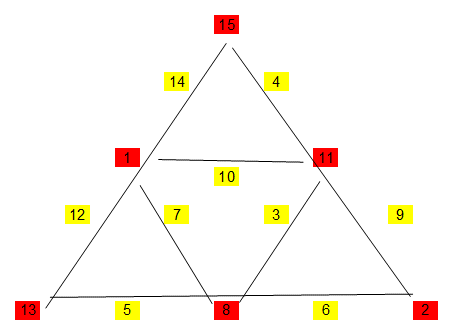
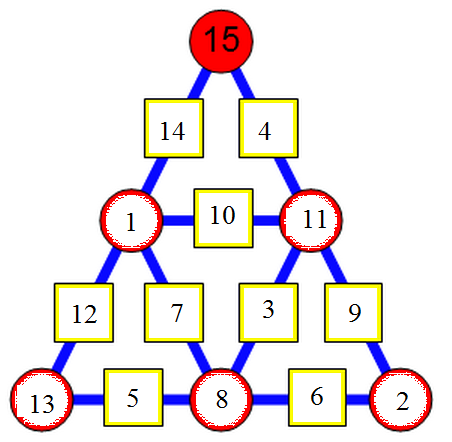
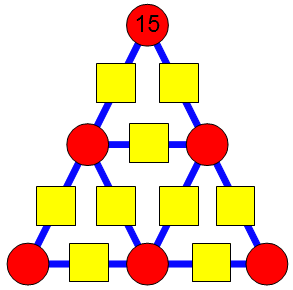
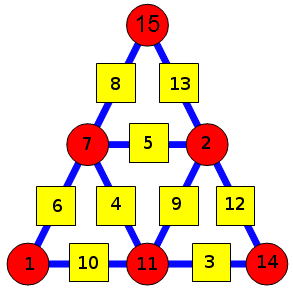
l'objectif de cette énigme est de placer les nombres de 1 à 15, une seule fois chacun, dans les cases du triangle ci-dessous, de telle sorte que chaque nombre écrit dans un carré soit égale à la différence des deux nombres écrits dans les deux cercles qui l'encadre.
Le 15 est déjà placé.
Si vous pensez qu'il n'y a pas de solution, vous répondrez "problème impossible".
S'il existe plusieurs solutions, vous n'en donnerez qu'une seule.
Bonne recherche ! 
 Bonjour jamo,
Bonjour jamo,
Voici une solution ; les nombres sont écrits une ligne après l'autre
[15]
[2, 8]
[13, 6, 7]
[1, 10, 4, 5]
[14, 11, 3, 9, 12]
Merci pour cette énigme de grille triangulaire.
 Bonjour
Bonjour
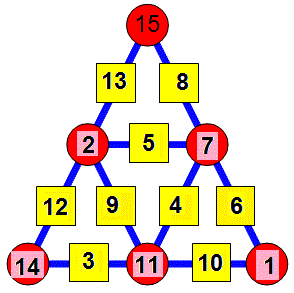
Voici une solution possible :
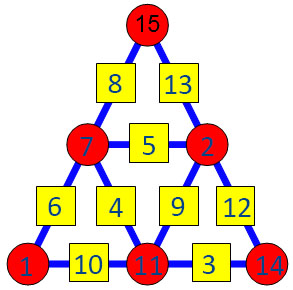
Apparemment il n'en existerait que 4 distinctes (à une symétrie près)
J'aurais -- a priori -- parié sur beaucoup plus, comme quoi...
Merci pour l'énigmo, et à bientôt
 Bonjour !
Bonjour !
Mon ordinateur trouve sans mal du tout la solution suivante :
15
13 8
2 5 7
12 9 4 6
14 3 11 10 1
et c'est loin d'être la seule (si des gens arrivent à trouver combien il y en a...)
Merci pour l'énigme !
 Bonjour!
Bonjour!
Je propose de placer
2 et 8 sur la 2eme ligne
13,6 et 7 sur la 3eme ligne
1,10,4 et 5 sur la 4eme ligne
14,11,3,9 et 12 sur la dernière ligne
Merci à Jamo!
 Bonjour Jamo,
Bonjour Jamo,
On peut déjà dire que si on fixe les nombres à l'intérieur des cercles, les nombres dans les carrés s'en déduisent.
Ma démarche :
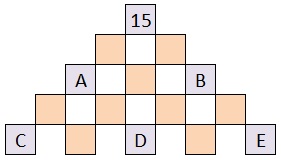
J'appelle A, B, C, D et E les nombres des cercles. Pour moi, ce seront les nombres de la partie grise. J'ai programmé des boucles imbriquées sous Maple qui calculent au fur et à mesure les nombres des carrés et les comparent aux nombres déjà présents.
J'ai écrit la fonction LecteurCourageux qui prend en argument un nombre et une liste, et retourne 1 si le nombre n'est pas dans la liste, 0 sinon.
LecteurCourageux:=proc(X,L)
local compteur,k:
compteur:=1:
for k from 1 to nops(L) do
if X=L[k] then compteur:=0:
fi:
od:
return compteur:
end proc:
Puis les boucles imbriquées, qui à chaque choix de A et B puis de C, .. E, regarde si les valeurs n'ont pas déjà été prises.
Remarques :
- Je précise au début de la boucle B<A, car on voit bien que la situation est, au départ, symétrique en A et B.
- Comme D est réservé à l'opérateur dérivée chez Maple, j'ai changé D en D2.
- Si on réfléchit un peu, il y a moyen de beaucoup le raccourcir.
- Les conditions au début de chaque boucle évitent de perdre beaucoup de temps dans des boucles inutiles (genre 1 1 ..)
Le code (bien sale hein, je ne l'ai pas maquillé) :
for A from 1 to 14 do
for B from 1 to 14 do
if A<>B and B<A and LecteurCourageux(15-A,[B,abs(A-B)])*LecteurCourageux(15-B,[A,abs(A-B)])*LecteurCourageux(abs(A-B),[A,B,15-A,15-B])=1 then
for D2 from 1 to 14 do
if LecteurCourageux(D2,[A,B,abs(A-B),15-A,15-B,abs(D2-A),abs(B-D2)])*LecteurCourageux(abs(D2-A),[A,B,D2,abs(B-A),15-A,15-B,abs(B-D2)])*LecteurCourageux(abs(B-D2),[A,B,D2,abs(B-A),15-A,15-B,abs(A-D2)])=1 then
for C from 1 to 14 do
if LecteurCourageux(C,[A,B,D2,15-A,15-B,abs(A-B),abs(A-D2),abs(B-D2),abs(A-C),abs(D2-C)])*LecteurCourageux(abs(A-C),[A,B,D2,15-A,15-B,abs(A-B),abs(A-D2),abs(B-D2),C,abs(D2-C)])*LecteurCourageux(abs(D2-C),[A,B,D2,15-A,15-B,abs(A-B),abs(A-D2),abs(B-D2),C,abs(A-C)])=1 then
for E from 1 to 14 do
if LecteurCourageux(E,[15-A,15-B,A,abs(A-B),B,abs(A-C),abs(A-D2),abs(B-D2),abs(B-E),C,abs(C-D2),D2,abs(D2-E)])*LecteurCourageux(abs(B-E),[15-A,15-B,A,abs(A-B),B,abs(A-C),abs(A-D2),abs(B-D2),E,C,abs(C-D2),D2,abs(D2-E)])*LecteurCourageux(abs(D2-E),[15-A,15-B,A,abs(A-B),B,abs(A-C),abs(A-D2),abs(B-D2),abs(B-E),C,abs(C-D2),D2,E])=1 then
print(A,B,C,D2,E):
fi: od: fi: od: fi: od: fi: od: od:
Résultats : Maple sort 4 séquences de nombres
1, 11, 13, 8, 2
2, 7, 14, 11, 1
2, 10, 14, 11, 4
7, 13, 12, 3, 14
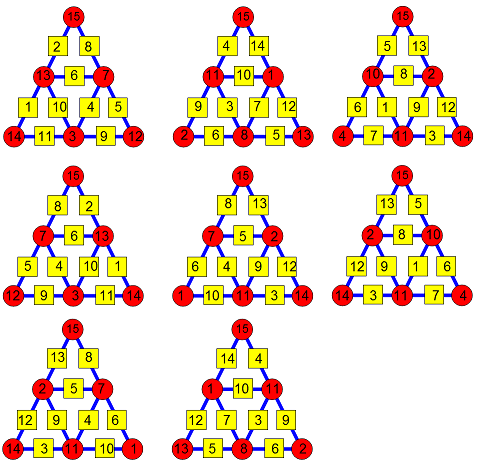
Ce qui donne les 4 triangles différents suivants [il y en a 4 autres ou A et B sont permutés, de même que C et E] :
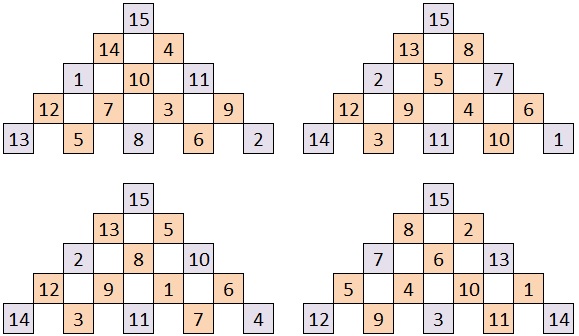
Jamo, si tu dois n'en retenir qu'un, le premier est ma proposition. En tout cas merci pour cette énigme, j'ai pris plaisir à programmer un peu (c'est très modeste) et d'avoir un résultat.

 Je développe un chouïa.
Je développe un chouïa.
J'ai essayé le pseudo-aléatoire et les permutations, ça n'a rien donné. Alors j'ai voulu faire des tests avec des triangles plus petits. Avec 6, ça marche :
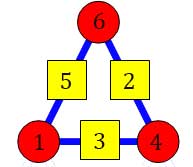
Alors je me suis dit : peut-être que ça ne marche qu'avec des nombres pairs.
Mais j'ai essayé avec 11 et il y a au moins une solution :
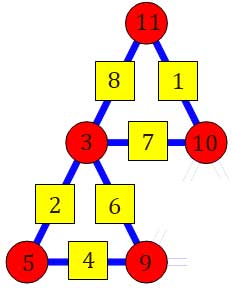
Donc apparemment rien ne prouve qu'il n'y en a pas pour 15, mais je n'en trouve aucune.
Tout au plus il est possible de faire en sorte qu'un seul carré ne respecte pas la condition (en bleu sur l'image) :
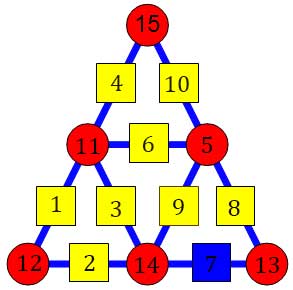
S'il s'avère qu'une solution existe (plus qu'à attendre), il faudra que je remette en question ma manière de programmer...
Peut-être qu'en ne fixant pas le 15 il existe une solution ? Je vais essayer.
 Bonjour,
Bonjour,
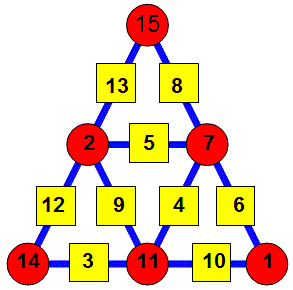
Je trouve 8 solutions (4 si on tient compte des symétries). En voici une (en image, pour une fois).
Merci pour l'énigme. 
 Il semble qu'il y ait 8 solutions en tout :
Il semble qu'il y ait 8 solutions en tout :
1 11 13 8 2 (celle que j'ai proposé)
et les 7 autres :
2 7 14 11 1
2 10 14 11 4
7 2 1 11 14
7 13 12 3 14
10 2 4 11 14
11 1 2 8 13
13 7 14 3 12
(Valeurs des cases rouges de gauche à droite et de haut en bas)
 Bonjour,
Bonjour,
en nommant A, B, C, D et E les valeurs des 5 ronds rouges, les autres valeurs sont déduites par le calcul.
Je trouve 4 combinaisons qui conviennent (en plus des 4 obtenues par symétrie verticale bien sûr).
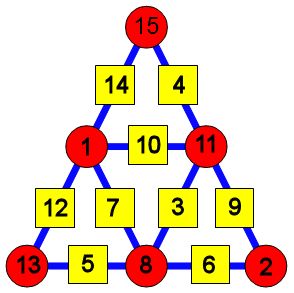
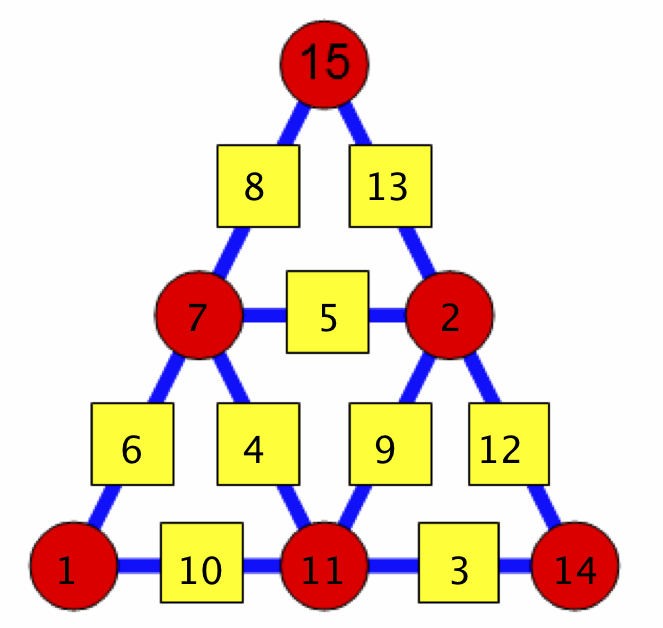
je propose par exemple la première des 4 solutions ci dessous:
A=1; B=11; C=13; D=8 et E=2 !
[img]
Merci et à la prochaine!

J'ai trouvé 4 réponses (+4 symétries). L'une d'elle est :
15
/ \
4 14
/ \
11 - 10 - 1
/ \ / \
9 3 7 12
/ \ / \
2 - 6 - 8 - 5 - 13
Merci pour l'énigme.
 8 solutions tout de même.
8 solutions tout de même. 
Ouais, sur les 14! combinaisons possibles, j'aurais eu du mal avec seulement le pseudo-aléatoire et les permutations. 
Je m'en vais jeter un coup d'il sur les algos de ceux qui ont partagé leur code, je ne vois absolument pas comment s'y prendre.
 @Alishisap,
@Alishisap,
Voici mon programme en fortran 90 :
Il n'est clairement pas optimisé, mais ça marche. Le principe : je place des nombres de 1 à 14 dans les cases en vérifiant que je ne met pas 2 fois le même. Selon le nombre de nombre placés, je vérifie que l'énoncé du problème soit respecté. Si j'ai deux fois le même nombre ou que la différence n'est pas vérifiée alors j'arrête la boucle en cours (grâce à un goto) et j'incrémente la boucle.
program test
implicit none
integer :: b,c,d,e,f,g,h,i,j,k,l,m,n,o
do b=1,14
do c=1,14
if (c==b) then
goto 1
end if
do d=1,14
if ((d==b).or.(d==c).or.(abs(d-15).ne.b)) then
goto 2
end if
do e=1,14
if ((e==b).or.(e==c).or.(e==d)) then
goto 3
end if
do f=1,14
if ((f==b).or.(f==c).or.(f==d).or.(f==e).or.(abs(d-f).ne.e).or.(abs(f-15).ne.c)) then
goto 4
end if
do g=1,14
if ((g==b).or.(g==c).or.(g==d).or.(g==e).or.(g==f)) then
goto 5
end if
do h=1,14
if ((h==b).or.(h==c).or.(h==d).or.(h==e).or.(h==f).or.(h==g)) then
goto 6
end if
do i=1,14
if ((i==b).or.(i==c).or.(i==d).or.(i==e).or.(i==f).or.(i==g).or.(i==h)) then
goto 7
end if
do j=1,14
if ((j==b).or.(j==c).or.(j==d).or.(j==e).or.(j==f).or.(j==g).or.(j==h).or.(j==i)) then
goto 8
end if
do k=1,14
if ((k==b).or.(k==c).or.(k==d).or.(k==e).or.(k==f).or.(k==g).or.(k==h).or.(k==i).or.(k==j).or.(abs(d-k).ne.g)) then
goto 9
end if
do l=1,14
if ((l==b).or.(l==c).or.(l==d).or.(l==e).or.(l==f).or.(l==g).or.(l==h).or.(l==i).or.(l==j).or.(l==k)) then
goto 10
end if
do m=1,14
if ((m==b).or.(m==c).or.(m==d).or.(m==e).or.(m==f).or.(m==g).or.(m==h).or.(m==i).or.(m==j).or.(m==k).or.(m==l) &
& .or.(abs(m-k).ne.l).or.(abs(m-d).ne.h).or.(abs(m-k).ne.l).or.(abs(m-f).ne.i)) then
goto 11
end if
do n=1,14
if ((n==b).or.(n==c).or.(n==d).or.(n==e).or.(n==f).or.(n==g).or.(n==h).or.(n==i).or.(n==j).or.(n==k).or.(n==l).or.(n==m)) then
goto 12
end if
do o=1,14
if ((o==b).or.(o==c).or.(o==d).or.(o==e).or.(o==f).or.(o==g).or.(o==h).or.(o==i).or.(o==j).or.(o==k).or.(o==l).or.(o==m) &
& .or.(o==n).or.(abs(o-f).ne.j).or.(abs(m-o).ne.n)) then
goto 13
end if
print*,15,b,c,d,e,f,g,h,i,j,k,l,m,n,o
13 continue
enddo !o
12 continue
enddo !n
11 continue
enddo !m
10 continue
enddo !l
9 continue
enddo !k
8 continue
enddo !j
7 continue
enddo !i
6 continue
enddo !h
5 continue
enddo !g
4 continue
enddo !f
3 continue
enddo !e
2 continue
enddo !d
1 continue
enddo !c
enddo !b
end program
 Bonjour Alishisap
Bonjour Alishisap
Non, en force brute on remplit les ronds rouges, (5 nombres) avec 5 boucles imbriqués avec les nombres restant libres. A chaque étape on vérifie la possibilité de remplir les carrés jaunes.
Au pire 14*13*12*11*10 possibilités,
mais comme on remplit les cases jaunes au fur et a mesure:
au pire 14*12*9*6*3 possibilités.
en pratique, beaucoup moins.
 Voici mon programme en Java, si ça intéresse quelqu'un. Comme d'habitude, j'utilise la récursivité.
Voici mon programme en Java, si ça intéresse quelqu'un. Comme d'habitude, j'utilise la récursivité. 
public class Enigmo302UnTriangleDifferent {
// Tableau des cases du triangle, de haut en bas et de gauche à droite
private static int[] triangle = new int[15];
private static List<Integer> utilises = new ArrayList<>();
public static void main(String[] args) {
triangle[0] = 15;
resoudre(1);
}
// noeud = numéro de la case à remplir
private static void resoudre(int noeud) {
for (int i = 1; i < 15; i++)
if (!utilises.contains(i)) {
triangle[noeud] = i;
utilises.add(i);
// Pour les oases rondes, on teste si les différences sont correctes
switch (noeud) {
case 3 :
if (correct(0, 1, 3))
resoudre(noeud + 1);
break;
case 5 :
if (correct(0, 2, 5) && correct(3, 4, 5))
resoudre(noeud + 1);
break;
case 10 :
if (correct(3, 6, 10))
resoudre(noeud + 1);
break;
case 12 :
if (correct(10, 11, 12) && correct(3, 7, 12) && correct(5, 8, 12))
resoudre(noeud + 1);
break;
case 14 : // Dernière case
if (correct(12, 13, 14) && correct(5, 9, 14))
afficherSolution();
break;
default : // Cases carrées, pas de test
resoudre(noeud + 1);
}
utilises.remove(utilises.size() - 1);
}
}
// Renvoie true si la case j est la différence entre les cases i et k.
private static boolean correct(int i, int j, int k) {
return Math.abs(triangle[k] - triangle[i]) == triangle[j];
}
private static void afficherSolution() {
int k = 0;
for (int i = 0; i < 5; i++) {
for (int j = 0; j <= i; j++) {
System.out.print(triangle[k++]+" ");
}
System.out.println();
}
}
}
 Merci !
Merci ! 
Donc si j'ai bien compris, le mieux c'est de :
- Remplir les 5 ronds avec 5 nombres différents.
- On en déduit les nombres dans les carrés.
- On vérifie que les nombres sont tous différents : si oui c'est bon, sinon on modifie les nombres dans les ronds et on reprend.
 Bonjour rijks,
Bonjour rijks,
Il reste encore des programmeurs en fortran! 
D'ici peu on retrouvera des programmeurs 2 ligneurs en APL.
J'ai utilisé la même méthode:
CONST Faux = (0 = 1)
CONST Vrai = NOT (Faux)
CONST ord = 15
DIM SHARED Tri(15) AS INTEGER, nbsol AS LONG
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER, t AS INTEGER, u AS INTEGER
OPEN "c:\_enigmo\302\302.sol" FOR OUTPUT AS #1
CALL Init
CALL Traiter
CLOSE #1
END
FUNCTION notInTri% (p AS INTEGER)
DIM ret AS INTEGER, i AS INTEGER
ret = Vrai
FOR i = 1 TO ord
IF Tri(i) = p THEN
ret = Faux
EXIT FOR
END IF
NEXT i
notInTri% = ret
END FUNCTION
SUB Traiter
DIM i2 AS INTEGER, i3 AS INTEGER, i4 AS INTEGER, i5 AS INTEGER, i6 AS INTEGER
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER
Tri(1) = ord
LOCATE 1, 21: PRINT Tri(1)
CALL Boucle1
END SUB
SUB Boucle1
DIM i2 AS INTEGER
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER
FOR i2 = 1 TO ord - 1
IF notInTri%(i2) THEN
Tri(4) = i2
x = ABS(15 - Tri(4))
IF notInTri%(x) THEN
Tri(2) = x
CALL Boucle2
Tri(2) = 0
END IF
Tri(4) = 0
END IF
NEXT i2
END SUB
SUB Boucle2
DIM i3 AS INTEGER
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER
FOR i3 = 1 TO ord - 1
IF notInTri%(i3) THEN
Tri(6) = i3
x = ABS(Tri(6) - Tri(4))
IF notInTri%(x) THEN
Tri(5) = x
y = ABS(15 - Tri(6))
IF notInTri%(y) THEN
Tri(3) = y
CALL Boucle3
Tri(3) = 0
END IF
Tri(5) = 0
END IF
Tri(6) = 0
END IF
NEXT i3
END SUB
SUB Boucle3
DIM i4 AS INTEGER
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER
FOR i4 = 1 TO ord - 1
IF notInTri%(i4) THEN
Tri(11) = i4
x = ABS(Tri(11) - Tri(4))
IF notInTri%(x) THEN
Tri(7) = x
CALL Boucle4
Tri(7) = 0
END IF
Tri(11) = 0
END IF
NEXT i4
END SUB
SUB Boucle4
DIM i5 AS INTEGER
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER
FOR i5 = 1 TO ord - 1
IF notInTri%(i5) THEN
Tri(13) = i5
x = ABS(Tri(13) - Tri(11))
IF notInTri%(x) THEN
Tri(12) = x
y = ABS(Tri(13) - Tri(4))
IF notInTri%(y) THEN
Tri(8) = y
z = ABS(Tri(13) - Tri(6))
IF notInTri%(z) THEN
Tri(9) = z
CALL Boucle5
Tri(9) = 0
END IF
Tri(8) = 0
END IF
Tri(12) = 0
END IF
Tri(13) = 0
END IF
NEXT i5
END SUB
SUB Boucle5
DIM i6 AS INTEGER
DIM x AS INTEGER, y AS INTEGER, z AS INTEGER
FOR i6 = 1 TO ord - 1
IF notInTri%(i6) THEN
Tri(15) = i6
x = ABS(Tri(15) - Tri(13))
IF notInTri%(x) THEN
Tri(14) = x
y = ABS(Tri(15) - Tri(6))
IF notInTri%(y) THEN
Tri(10) = y
CALL SeeTri
Tri(10) = 0
END IF
Tri(14) = 0
END IF
Tri(15) = 0
END IF
NEXT i6
END SUB
FUNCTION Net3$ (p AS INTEGER)
Net3$ = RIGHT$(SPACE$(3) + STR$(p), 3)
END FUNCTION
SUB SeeTri
SHARED Tri() AS INTEGER, nbsol AS LONG
DIM i AS INTEGER, f AS STRING
nbsol = nbsol + 1
f = STR$(nbsol) + ":" + CHR$(13)
f = f + SPACE$(3) + SPACE$(3) + SPACE$(3) + SPACE$(3) + Net3$(Tri(1)) + CHR$(13)
f = f + SPACE$(3) + SPACE$(3) + SPACE$(3) + Net3$(Tri(2)) + SPACE$(3) + Net3$(Tri(3)) + CHR$(13)
f = f + SPACE$(3) + SPACE$(3) + Net3$(Tri(4)) + SPACE$(3) + Net3$(Tri(5)) + SPACE$(3) + Net3$(Tri(6)) + CHR$(13)
f = f + SPACE$(3) + Net3$(Tri(7)) + SPACE$(3) + Net3$(Tri(8)) + SPACE$(3) + Net3$(Tri(9)) + SPACE$(3) + Net3$(Tri(10)) + CHR$(13)
f = f + Net3$(Tri(11)) + SPACE$(3) + Net3$(Tri(12)) + SPACE$(3) + Net3$(Tri(13)) + SPACE$(3) + Net3$(Tri(14)) + SPACE$(3) + Net3$(Tri(15)) + CHR$(13)
f = f + CHR$(13)
PRINT f
PRINT #1, f
END SUB
SUB Init
SHARED Tri() AS INTEGER, nbsol AS LONG
DIM i AS INTEGER
nbsol = 0
FOR i = 1 TO ord
Tri(i) = 0
NEXT i
n = 0
END SUB
 Bonjour,
Bonjour,
>>>Alishisap
Si on décide de déterminer les 6 nombres dans les ronds rouges ( sauf le 15), donc 5 nombres parmi les 14 restants, on a un nombre de solutions qui vaut le nombre d'arrangements A145= n!/(n-k)! =14!/9!= 240240 solutions possibles théoriquement.Les nombres dans les carrés étant automatiquement déterminés.
Personnellement, j'ai cherché "à la main" avec Excel.
1°) j'ai choisi de déterminer les 2 nombres dans les ronds rouges en-dessous du 15 donnés par les arrangements A142=14!/12! = 182 solutions possibles - réduites avec les impossibilités à +/- 160 - Ainsi 6 nombres étaient déterminés !
2°) ensuite j'ai déterminé les solutions pour le nombre dans le rond rouge inférieur gauche - Il restait 9 nombres. Pour ce nombre il y avait
A91= 9!/8! = 9 possibilités à multiplier par 160 soit 1440 solutions théoriques. Après échantillonnage il restait 891 solutions. Etaient alors déterminés 9 nombres
3°) j'ai déterminé le nombre de solutions pour le rond inférieur central
le nombre de solutions possibles était de A71 soit 7 solutions à multiplier par 891 = 6237 solutions
4°) 12 nombres étaient déterminés. Pour chacune des solutions possibles parmi les 6237 il était facile de trouver les 3 possibilités restantes
Ce fut long mais raisonnable
Amitiés
 Bonjour,
Bonjour,
avec un programme super basique (parce que je ne sais toujours pas faire autre chose qu'algobox!):
1 VARIABLES
2 a EST_DU_TYPE NOMBRE
3 b EST_DU_TYPE NOMBRE
4 c EST_DU_TYPE NOMBRE
5 d EST_DU_TYPE NOMBRE
6 e EST_DU_TYPE NOMBRE
7 f EST_DU_TYPE NOMBRE
8 g EST_DU_TYPE NOMBRE
9 h EST_DU_TYPE NOMBRE
10 i EST_DU_TYPE NOMBRE
11 j EST_DU_TYPE NOMBRE
12 k EST_DU_TYPE NOMBRE
13 l EST_DU_TYPE NOMBRE
14 m EST_DU_TYPE NOMBRE
15 n EST_DU_TYPE NOMBRE
16 p EST_DU_TYPE NOMBRE
17 q EST_DU_TYPE NOMBRE
18 r EST_DU_TYPE NOMBRE
19 s EST_DU_TYPE NOMBRE
20 t EST_DU_TYPE NOMBRE
21 u EST_DU_TYPE NOMBRE
22 DEBUT_ALGORITHME
23 POUR a ALLANT_DE 1 A 14
24 DEBUT_POUR
25 POUR b ALLANT_DE 1 A 14
26 DEBUT_POUR
27 POUR c ALLANT_DE 1 A 14
28 DEBUT_POUR
29 POUR d ALLANT_DE 1 A 14
30 DEBUT_POUR
31 POUR e ALLANT_DE 1 A 14
32 DEBUT_POUR
33 f PREND_LA_VALEUR abs(15-a)
34 g PREND_LA_VALEUR abs(15-b)
35 h PREND_LA_VALEUR abs(b-a)
36 i PREND_LA_VALEUR abs(c-a)
37 j PREND_LA_VALEUR abs(d-a)
38 k PREND_LA_VALEUR abs(b-d)
39 l PREND_LA_VALEUR abs(b-e)
40 m PREND_LA_VALEUR abs(c-d)
41 n PREND_LA_VALEUR abs(e-d)
42 p PREND_LA_VALEUR (a-b)*(a-c)*(a-d)*(a-e)*(a-f)*(a-g)*(a-h)*(a-i)*(a-j)*(a-k)*(a-l)*(a-m)*(a-n)
43 q PREND_LA_VALEUR (b-c)*(b-d)*(b-e)*(b-f)*(b-g)*(b-h)*(b-i)*(b-j)*(b-k)*(b-l)*(b-m)*(b-n)
44 r PREND_LA_VALEUR (c-d)*(c-e)*(c-f)*(c-g)*(c-h)*(c-i)*(c-j)*(c-k)*(c-l)*(c-m)*(c-n)
45 s PREND_LA_VALEUR (d-e)*(d-f)*(d-g)*(d-h)*(d-i)*(d-j)*(d-k)*(d-l)*(d-m)*(d-n)
46 t PREND_LA_VALEUR (e-f)*(e-g)*(e-h)*(e-i)*(e-j)*(e-k)*(e-l)*(e-m)*(e-n)*(f-g)*(f-h)*(f-i)*(f-j)*(f-k)*(f-l)*(f-m)*(f-n)
47 u PREND_LA_VALEUR (g-h)*(g-i)*(g-j)*(g-k)*(g-l)*(g-m)*(g-n)*(h-i)*(h-j)*(h-k)*(h-l)*(h-m)*(h-n)*(i-j)*(i-k)*(i-l)*(i-m)*(i-n)*(j-k)*(j-l)*(j-m)*(j-n)*(k-l)*(k-m)*(k-n)*(l-m)*(l-n)*(m-n)
48 SI (p*q*r*s*t*u*!=0) ALORS
49 DEBUT_SI
50 AFFICHER p
51 AFFICHER ";;;"
52 AFFICHER a
53 AFFICHER b
54 AFFICHER c
55 AFFICHER d
56 AFFICHER e
57 AFFICHER "--------------------------------------"
58 FIN_SI
59 FIN_POUR
60 FIN_POUR
61 FIN_POUR
62 FIN_POUR
63 FIN_POUR
64 FIN_ALGORITHME
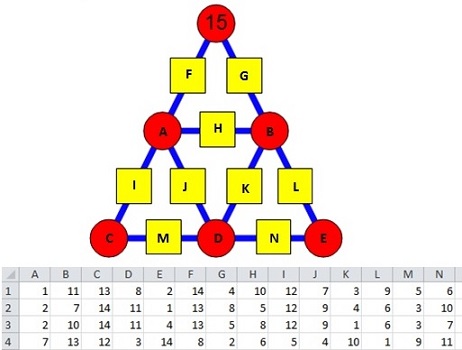
 Puisque vous en êtes à expliquer comment vous avez fait, je vous montre ma solution.
Puisque vous en êtes à expliquer comment vous avez fait, je vous montre ma solution.
J'ai simplement fait sous Excel la grille suivante :
Avec rien pour l'instant dans les cases jaunes (sauf le 15) et dans les cases blanches, des formules genre =ABS(F1-D3) (pour E2 par exemple).
Et puis
Avec dans la colonne L une copie des valeurs de toutes les cases
et dans la colonne O une formule =NB.SI($L$1:$L$15;N1) (pour O1) qui compte le nombre de fois où le chiffre de la colonne N apparaît. On a trouvé la solution quand toutes ces valeurs valent 1.
Puis j'ai écris la petite macro suivante :
Sub processus()
Dim I, J, K, L, M, N, P As Integer
Dim Oui As Boolean
For I = 1 To 14
Cells(3, 4) = I
For J = 1 To 14
If J <> I Then
Cells(3, 8) = J
For K = 1 To 14
If K <> J And K <> I Then
Cells(5, 2) = K
For L = 1 To 14
If L <> K And L <> J And L <> I Then
Cells(5, 6) = L
For M = 1 To 14
If M <> L And M <> K And M <> J And M <> I Then
Cells(5, 10) = M
Calculate
Oui = True
For P = 1 To 15
If Cells(P, 15) <> 1 Then Oui = False
Next P
If Oui Then Stop
End If
Next M
End If
Next L
End If
Next K
End If
Next J
Next I
End Sub
Voilà, ça tourne 20 seconde et ça affiche la solution.
salut
juste une question :: la fonction "calculate" effectue les formules de ta feuille, si je comprends bien la chose ?
merci par avance ...

Nombre de participations : 0
Temps de réponse moyen : 87:44:05.