Inscription / Connexion Nouveau Sujet
Enigmo 41 : Ma courbe bien-aimée 


Bonjour,
voici une petite énigme d'un nouveau genre. Si elle a du succès, on pourra en envisager de similaires.
Même si l'énigme semble très "mathématique", elle ne demande pas de connaissances très évoluées : si on comprend l'énoncé, on doit pouvoir la résoudre.
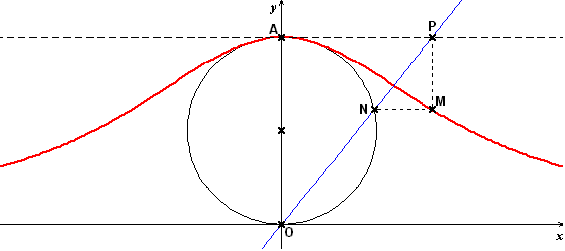
Dans un repère orthonormal d'origine O, on considère le point A de coordonnées (0;a) avec a>0, le cercle C de diamètre [OA], et la droite horizontale D d'équation y=a.
Pour toute droite non horizontale passant par le point O (en bleu sur le dessin), on définit le point N sur le cercle C et le point P sur la droite D.
On définit ensuite le point M en prenant l'abscisse du point P et l'ordonnée du point N.
Lorsque la droite bleue "tourne" autour du point O, le point M se balade donc sur une courbe, en rouge sur le dessin.
Question : donner l'équation de la courbe rouge. Cette équation doit être donnée sous forme explicite, où y est exprimé en fonction de x et du paramètre a : y=f(x,a). Aucun autre paramètre ne doit donc intervenir.
Bonne recherche ! 
Question subsidiaire : quel est le nom de cette courbe ?
 Soient (t,r) les coordonnées polaires du point N: on a donc r=asint. P a donc pour coordonnées (a/tant, a) et M: (x=a/tant,y=a(sint)^2. et comme (sint)^2/(tant)^2=1-(sint)^2
Soient (t,r) les coordonnées polaires du point N: on a donc r=asint. P a donc pour coordonnées (a/tant, a) et M: (x=a/tant,y=a(sint)^2. et comme (sint)^2/(tant)^2=1-(sint)^2
yx^2/a^2=a-y, donc
y=a^3/(a^2+x^2)
Je pense que c'est une cubique circulaire, mais mes souvenirs sont loin...
 bonjour
bonjour
on arrive à y = a^3/(a²+x²)
qui est la cubique d'Agnesi,( Maria Gaetana Agnesi est une des premières femmes mathématiciennes italienne du 18° )
Elle ressemble à la versiera ou la visiera ou à la conchoïde de Külp
Cependant, cette courbe avait été préalablement étudiée par Fermat

 salut Jamo,
salut Jamo,
Personnellement j'ai adoré cette énigme, j'espère que il y en aura d'autre 
Allé pour la peine je me lance dans une demo 
N appartient au cerle de centre et et rayon
Donc les coordonnées de N obeissent a :
La droite (D) à pour équation : y = bx or N appartient à (D) et a C
Donc N vérifie :
Car yM = yN
Or P appartient à (D) et à y = a, donc :
On conclut : , donc
Car xM = xP
(1) et (2) =>
Donc M décrit la fonction :

 Bonjour,
Bonjour,
Je trouve ; après une petite recherche, cette courbe s'appelle la cubique d'Agnesi, ou witch of Agnesi en anglais (http://www.mathcurve.com/courbes2d/agnesi/agnesi.shtml)... ce qui explique le titre de l'énigme !
Quelques étapes du calcul :
Soit (x,y) les coordonnées de M, et soit x_N l'abscisse de N.
On a d'abord : .
Et comme N est un point du cercle C, on a : .
Reste à extraire y de l'expression.
BA.
 Salut jamo.
Salut jamo.
L"équation de la courbe rouge est
Quant au nom de la courbe, je n'en sais rien, je vais aller voir sur Wiki...
@+ et merci pour l'énigme!
 bonjour jamo
bonjour jamo
je vais essayer de ne pas me laisser déborder ce mois ci
pour équation de la courbe en rouge je trouve
c'est la cubique (sorcière) de Maria Agnesie
merci et bonnes vacances
 Bonjour Jamo, et merci pour cette jolie courbe!
Bonjour Jamo, et merci pour cette jolie courbe!
Ayant formé l'équation du cercle, on a sans problème les coordonnées de N en fonction de celles de P. Comme l'abscisse x de M est celle de P et l'ordonnée y de M est celle de N on a immédiatement l'équation de la courbe:
.
Il s'agit de la cubique d'Agnesi (du nom d'une mathématicienne italienne).
 Bonjour,
Bonjour,
rapido (et bourrin), en passant par les coordonnées de N et P en fonction d'un paramètre b (issu de la droite d'équation y=bx), on a:
N() et P(
)
D'où M() puis finalement en éliminant le paramètre b, l'équation cartésienne y=
.
Merci pour l'exercice !
 Re-bonjour jamo,
Re-bonjour jamo,
Les coordonnées des points N et P sont:
Les coordonnées du point M sont donc:
or
L'équation de la courbe est donc:
Pour ce qui est de son nom, je l'appellerais bien "attention où tu mets les pieds, y a une bosse dans le tapis".
 Bonjour,
Bonjour,
On pose x et y les coordonnées du point M.
Le triangle OAP est rectangle en A, donc OA² + AP² = OP²
Le triangle OAN est rectangle en N, donc ON² + NA² = OA²
Le triangle ANP est rectangle en N, donc AN² + NP² = AP²
On sait aussi que ON + NP = OP soit ON² + NP² + 2.ON.NP = OP²
On a également OA = a et AP = x
donc :
a² + x² = OP²
ON² + NA² = a²
AN² + NP² = x²
soit ON² + 2NA² + NP² = OP²
et comme ON² + NP² + 2.ON.NP = OP²
on peut en déduire que NA² = ON.NP
Si on définit un point H, intersection des droites (OA) et (MN), on a un triangle OHN rectangle en H, avec OH = y
Et si on note  l'angle formé par les droites (OA) et (OP), les relations trigonométriques dans les triangles rectangles OAN et OHN nous donnent la relation suivante :
l'angle formé par les droites (OA) et (OP), les relations trigonométriques dans les triangles rectangles OAN et OHN nous donnent la relation suivante :
cos =
= =
soit ON² = a.y
Sachant que les droites (MN) et (AP) sont parallèles, le théorème de Thalès nous donne la relation suivante dans le triangle OAP :
=
soit
=
soit y =
a
En élevant au carré cette relation, on obtient :
y² = a²
Sachant que ON² = a.y et que OP² = a² + x²
on obtient la relation suivante :
Et pour ce qui est du nom de la courbe... j'espère que la subsidiaire n'est pas éliminatoire 
 bonjour
bonjour
soit g l'angle POX
AP = a*cos(g)
les angles OAN et POX ayant les côtés perpendiculaires chacun à chacun sont égaux : ON = a*sin(g)
l'ordonnée de N est ON*sin(g) = a*sin²(g)
pour tout x, g = arccos(x/a)
y = f(x,a) = a * sin²(arccos(x/a))
 soit X=AP
soit X=AP
f(X,a)=a-PM
on cherche l'ordonnée du point N
=> intersection du cercle et de la droite
cercle: x^2+(y-a/2)^2=(a/2)^2
droite: y=(a/X)x
=> x^2(1+a^2/X^2)-a^2x/X=0 => x(x(1+a^2/X^2)-a^2/X)=0
=> x=0 ou x=(a^2X)/(X^2+a^2)
la deuxieme solution est interessante
elle a pour ordonnée: y=a^3/(x^2+a^2)
Donc f(a,x)=a^3/(x^2+a^2)
 Bonjour
Bonjour 
La courbe rouge a pour équation
Le cercle a pour équation paramétrique
Ainsi la droite
L'équation de la droite
Elle coupe la droite
Puisque le point
En reportant
Or on a
Elevons cette égalité au carré :
Par ailleurs
On reporte dans l'égalité précédente :
La courbe correspondant à cette équation est tracée en rouge pointillé sur le graphique ci-dessous et coïncide bien avec le lieu de points représenté en jaune. La fonction est bien paire par symétrie, vaut
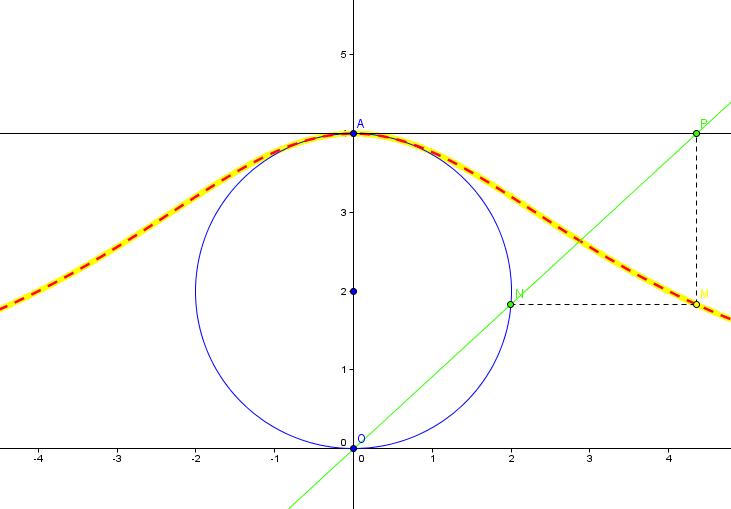
On peut s'amuser à calculer l'aire sous la courbe
Par conséquent
On peut également calculer la courbure au point
On trouve pour
On en déduit que le cercle bleu est le cercle de courbure au point
Quant au nom de la courbe en question je n'en ai aucune idée, ça me fait penser à une enveloppe

Merci pour l'énigme fort intéressante !

 salut,
salut,
bon en utilisant talès(ou bien les cos et les sin dse triangles rectangles) et l'equation d'un cercle je trouve: y=a^5/(x²-a^4).
cordialement;
Lotfi
 Soit x l'abscisse de P et y l'ordonnée de N
Soit x l'abscisse de P et y l'ordonnée de N
Et M a pour coordonnées (x ; y)
On cherche y = f(x)
La droite pivotante a pour équation aX = xY
Le cercle C a pour équation X² + (Y - a/2)² = a²/4
L'intersection des 2, c'est N de coordonnées :
(xN = 0 et y = 0) ou (xN = a²x/(a²+x²) et y = a^3/(a²+x²))
On trouve donc y = a^3 /(x²+a²)
 je défini les angles w1 et w2 (voir schéma)
je défini les angles w1 et w2 (voir schéma)
on a alors :
et
la relation entre w1 et w2 est:
donc en remplaçant on obtient:
soit
Cette courbe fait partie des courbes de Gauss
 Bonsoir,
Bonsoir,
J'ai trouvé
On pourrait aussi écrire de façon plus homogène :
J'ignore le nom de cette courbe !

à mon avis l'équation de la courbe des points M a pour équation :
f(x,a): y = a^3 /(x² + a²)
par contre aucune idée pour ce qui est du nom !
 Bonsoir:
Bonsoir:
Personnellement j'aime bien ce genre de problèmes! Bingo!
alors sans être vraiment explicatif, soit une fonction f qui définit la courbe représentée: pour tout x réel:
Bonnes continuation!
 Bonjour,
Bonjour,
La droite D a pour équation : avec m réel
Le cercle C a pour équation :
Les coordonnées de N sont obtenues par résolution du systéme :
De même pour le point P avec :
Soit :
Le point M a donc pour coordonnées :
Après quelques essais, on arrive très vite à trouver la relation suivante :
D'où finalement l'équation finale :
Question subsidiaire : Il me semble qu'une telle courbe est appelée courbe serpentine, mais sans conviction 
Voilà, sauf erreur de ma part. Merci pour l'énigme 
 J'ai dû faire une bêtise ça colle pas finalement... Tant pis c'est le jeu.
J'ai dû faire une bêtise ça colle pas finalement... Tant pis c'est le jeu.
Voilà sinon j'ai adoré cette énigme  donc en ce qui me concerne j'approuve le :
donc en ce qui me concerne j'approuve le :
voici une petite énigme d'un nouveau genre. Si elle a du succès, on pourra en envisager de similaires.
A bientôt
 Et voilà, j'aurais dû attendre au lieu d'avoir peur que l'énigme soit clôturée...
Et voilà, j'aurais dû attendre au lieu d'avoir peur que l'énigme soit clôturée...
Tant pis au moins pour pas être ridicule je mets le résultat pour le fun :
Dommage ...
 Salut!
Salut!
Je sais que c'est la sorcière d'Agnesi mais de là à donner son équation... c'est bizard, je connais le nom et pas l'équation!?
c'est bizard, je connais le nom et pas l'équation!?
Je crois que je vais aller sur wikipédia
A+
 La courbe a pour équation
La courbe a pour équation .
Il s'agit de la Cubique d'Agnesi.
Je dois bien avouer, je l'ai trouvée sur le net. Perso, j'arrivais à la courbe paramétrée mais j'avais du mal à repasser en expression explicite.
 Bonjour tout le monde,
Bonjour tout le monde,
bon, je me lance, j'essaye d'insérer une image.
celle ci apparait bien en dessous du message mais pas dans l'aperçu.
j'ai seulement défini un point H qui est la projection de N (ou de M) sur l'axe Oy:
OH = y HN = z HM = x
je pars de l'équation classique du cercle dans un repère ayant pour origine le centre du cercle.
soit R le rayon du cercle avec
soit z et y les coordonnées de N
x et y étant les coordonnées de M
dans le repère l'équation de notre cercle devient
d'où je tire
d'autre part avec les triangles OAP et OHN (merci Thalès) on a :
j'obtiens donc 2 équations:
en remplaçant R par j'obtiens la formule finale et ma réponse:
Question subsidiaire:
entre les tractoires, les tractrices, la courbe de l'âne et tout ce qui est en ...oïde j'ai pas trouvé.
 Appelons
Appelons  l'angle que fait la droite D avec l'axe des abscisses.
l'angle que fait la droite D avec l'axe des abscisses.
L'équation en coordonnées polaires du cercle C est R=a sin( ). Les coordonnées de N seront Xn=a sin(
). Les coordonnées de N seront Xn=a sin( )cos(
)cos( ) et Yn=a sin²(
) et Yn=a sin²( )
)
Les coordonnées de P sont Xp=a/tg( ) et Yp=a
) et Yp=a
Les coordonnés de M sont donc Xm=XP=a/tg( ) et Ym=Yn=a sin²(
) et Ym=Yn=a sin²( )=a(1-cos(2
)=a(1-cos(2 ))/2
))/2
Appelons tg( )=t , d'après la formule de l'angle moitié on a cos(2
)=t , d'après la formule de l'angle moitié on a cos(2 )=(1-t²)/(1+t²)
)=(1-t²)/(1+t²)
On a ainsi Ym=a(1-(1-t²)/(1+t²))/2=at²/(1+t²)
Or Xm=a/tg( )=a/t d'où t=a/x
)=a/t d'où t=a/x
En remplaçant on obtient Ym=a3/(a²+x²)
Question subsidiaire
Selon les sources cette courbe s'appelle la cubique (ou la versière) d'Agnesi, les anglais parlent de « Witch of Agnesi », les italiens de « Versiera d'Agnesi » (versiera=diablesse en italien)
 Bonjour,
Bonjour,
L'équation de la courbe rouge est
Question subsidiaire : On appelle cette courbe sorcière d'Agnesi ou verseau.
Merci et A+, KiKo21.
 Bonjour,
Bonjour,
Une courbe de Gauss?  n'importe quoi!
n'importe quoi!
De plus, j'ai oublié le point A: pour x = 0, y = a, of course 
Encore un mois de juillet qui sent le 
A+, 
Cloture de l'énigme
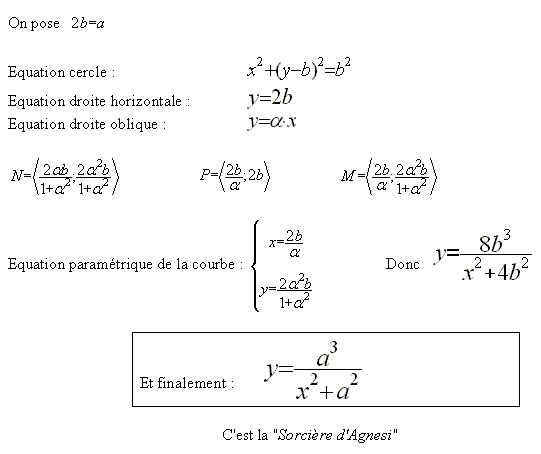
Il s'agissait donc de la "Sorcière d'Agnesi", ce qui expliquait le titre de l'énigme 
On peut trouver des infos ici par exemple : ![]()
J'ai accepté la réponse de plumemeteore car elle est correcte (un smiley spécial "pourkouafersimplekanonpeufercompliké" ) 
Par contre, la réponse de totti1000 est fausse : j'ai essayé de tracer sa fonction, et ça ne marche pas.
Et voilà l'image que je n'avais pas osé mettre dans le sujet de l'énigme, cela aurait été un indice trop important.

 Bonjour,
Bonjour,
> Jamo
voici une petite énigme d'un nouveau genre. Si elle a du succès, on pourra en envisager de similaires.
Alors on pourra... C'était vraiment très intéressant à étudier.
Et voilà l'image que je n'avais pas osé mettre dans le sujet de l'énigme, cela aurait été un indice trop important.
Effectivement !!
Encore merci et A+, KiKo21.
 bonjour
bonjour
>kévin
Dans tes suppléments, tu peux alors chercher à calculer le volume du solide de révolution obtenu en faisant tourner la courbe autour de son asymptote horizontale...
A toi

 Dommage que d'excellents sites dont les liens ont été donnés dans les réponses des participants ( ceux de Serge MEHL ou Robert FERRÉOL ou ... ) référencent toutes ces courbes avec même, pour certaines, le détail d'obtention des équations
Dommage que d'excellents sites dont les liens ont été donnés dans les réponses des participants ( ceux de Serge MEHL ou Robert FERRÉOL ou ... ) référencent toutes ces courbes avec même, pour certaines, le détail d'obtention des équations 

Nombre de participations : 0
Temps de réponse moyen : 91:59:23.

 0,
0,