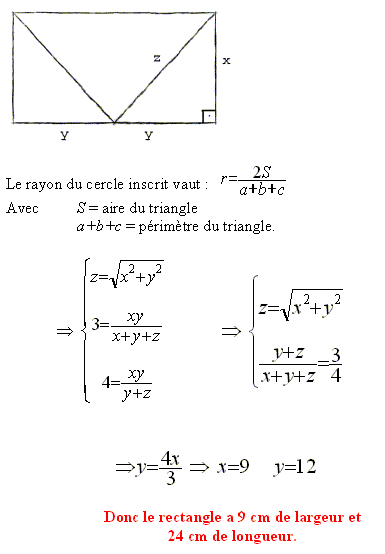Inscription / Connexion Nouveau Sujet
Enigmo 8 : Les souris géomètres 


Bonjour,
toutes les carottes de mon jardin ont été dévorées par des souris qui ont creusées des tunnels sous la terre !
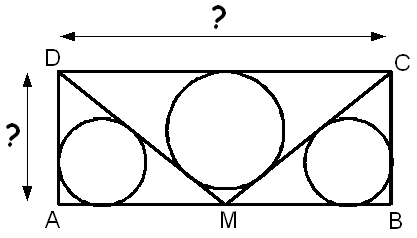
En creusant, j'ai découvert que les souris se déplaçaient dans trois petits tunnels : le plus gros, au milieu, fait 4cm de rayon, et les deux plus petits, de part et d'autre, font 3cm de rayon.
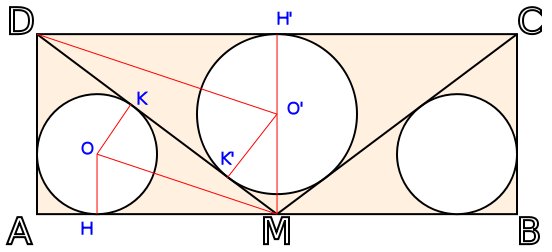
Chose étonnante : les trois tunnels sont tangents aux côtés d'un rectangle ABCD, et tangents aux segments [MC] et [MD], où M est le milieu de [AB] (voir figure ci-dessous).
Si vous me donnez les dimensions exactes du rectangle (la longueur et la largeur), alors peut-être que j'épargnerai ces satanées souris ...
Facultatif : une petite démonstration du résultat serait intéressante, dans le but de comparer les différentes méthodes.

 Bonjour,
Bonjour,
On note la largeur du rectangle et
sa longueur.
Le rayon du cercle inscrit dans un triangle est donné par la formule
où S est l'aire du triangle et P son périmètre.
(formule trouvée sur Wikipédia  )
)
Ce qui nous donne les deux équations suivantes :
pour les triangles AMD et CMB,
pour le triangle DMC.
Après simplifications, on obtient :
Ce qui donne :
La solution étant exclue, on arrive donc à la relation
.
En remplaçant par
dans une des équations de départ, on obtient :
Donc, les dimensions exactes du rectangle sont :
 J'ai utilisé une méthode analytique en mettant le centre du repère en M.
J'ai utilisé une méthode analytique en mettant le centre du repère en M.
Soient 2X et Y la longueur et la largeur du rectangle.
Je calcule l'équation des deux droites DM et CM et je traduis le fait que les points de coordonnées (-X+3,3) et par symétrie (X-3,3) sont à une distance de 3 par rapport à ces droites.
J'obtiens la relation : 6X+6Y=18+XY
Je traduis aussi que le point de coordonnées (0,Y-4) est à une distance de 4 par rapport à ces droites. J'obtiens la relation X2Y-8X2=16Y
En combinant ces deux équations, j'obtiens une équation du 3ème degré en X dont la solution est 12, ce qui donne Y=9.
Les dimensions du rectangle sont donc 24 cm et 9 cm.
 Bonjour à toutes et à tous!
Bonjour à toutes et à tous!
Je trouve pour le rectangle
une longueur de 24 cm et une largeur de 9cm.
Je n'ai pas vérifié (il faut vivre dangereusement)!
(j'ai quand même fait un dessin à l'échelle, qui a l'air de coller)
Je fais cela analytiquement, en choisissant le repère d'origine A qui me tend les bras.
La droite DM a une équation de la forme
, avec
En écrivant que sa distance au centre du petit cercle est 3, je détermine d en fonction de .
En écrivant que sa distance au centre du grand cercle est 4, je forme l'équation donnant :
, qui n'a qu'une solution (évidente?) :
et
Je reporte dans les coordonnées de D et M pour avoir la largeur et la demi-longueur.
Le résultat est si simple que je me demande si il n'y a pas une méthode plus simple. Je vais chercher...
 Salut,
Salut,
Ma réponse:
Le rectangle mesure exactement 9cm de large pour 24 cm de long
Pourquoi? D'abord heuseusement que c'est facultatif, parce que c'est un peu au pif, et deuxièmement car j'ai suposé que l'angle ADM était Tg(-1) de 3/4 étant donné le rapports entre les cercles.
On verra si c'est ca!
J'espere en tout cas
@ plus, Chaudrack
 Bonjour
Bonjour
On sait que l'aire d'un triangle est donnée par pr avec p le demi-périmètre et r le rayon du cercle inscrit
soit N le point de contact du cercle de rayon 4 avec DC
soient AB = DC = 2AM = 2DN = x et AD = MN = BC = y et DM = MC = (x²/4 + y²)
(x²/4 + y²)
on a
aire DCM = (DC/2 + DM)*4 = DC.MN/2 => (x/2 + DM)*4 = xy/2 => DM = (xy - 4x)/8
aire ADM = [(AD + DM + AM)/2].3 = AM.AD/2 => (y + DM + x/2).3 = (x/2).y => DM = (xy/2 - 3y -3x/2)/3
=> (xy - 4x)/8 = (xy/2 - 3y -3x/2)/3 => 3xy - 12x = 4xy - 24y - 12x => x = 24
et avec DM =  (x²/4+y²) = x(y-4)/8 on a
(x²/4+y²) = x(y-4)/8 on a  (24²/4+y²) = 3(y-4) => 144 + y² = 9(y² - 8y + 16) => 8y² - 72y = 0 => y² - 9y = 0 => y = 9
(24²/4+y²) = 3(y-4) => 144 + y² = 9(y² - 8y + 16) => 8y² - 72y = 0 => y² - 9y = 0 => y = 9
=>
AB = x = 24 et AD = y = 9
ET Cabri 2+ me l'a confirmé.
A+
 Bonjour,
Bonjour,
Enigme interessante, mais les calculs sont épouvantables. Je suppose que des considérations géométriques m'auraient aidé 
Soit L la longueur (L=AB) et h la largeur (h=AD) du rectangle en cm.
la droite MC admet pour équation y=-(2h/L)x+h, si on place l'origine en A.
Le cercle tangent aux segments AD et AM admet pour équation (x-3)²+(y-3)²=9
Ecrivons que la droite MC et le cercle sont tangents l'un à l'autre.
(x-3)²+(-(2h/L)x+h-3)²=9 admet une solution unique.
x²(1+(2h/L)²)+x(-6+12h/L-4h²/L)+(h²+9-6h)=0
La solution est unique si
(-6+12h/L-4h²/L)²-4(1+(2h/L)²)(h²+9-6h)=0
Le cercle de rayon 4 admet pour équation (x-L/2)²+(y-h+4)²=16
L'équation (x-L/2)²+(-(2h/L)x+4)²=16 admet une solution unique.
x²(1+(2h/L)²)-x(L+16h/L)+L²/4=0
La solution est unique si
(L+16h/L)²-L²(1+(2h/L)²)=0
A l'aide d'un solveur, je trouve AB=24cm et AD=9cm
Il faudra que je réfléchisse à une méthode moins brutale
 bonjour,
bonjour,
je donne d'abord ma réponse,je trouve
AB=24cm ,BC=9cm
je pose CB=x,MB=y
a)dans le triangle rectangle MBC:
longueurs des segments de tangentes au cercle de rayon 3cm
CI et CJ issues de C : ( x-3 )cm
BI et BK issues de B :3cm
MK et MJ issues de M : (y-3) cm
MC=MJ+JC=(y-3)+(x-3)=x+y-6 (1)
mais MC²=MB²+BC²= y²+x² (2)
(1) et(2)=> (x+y-6)²=x²+y² soit 2xy-12(x+y)+36=0 xy-6(x+y)+18=0 (3)
M'......................C
. .
. .
. .(x-3)
. .
. .
. J .
. I
. .3
. .
M..............K......B
< y >
b) dans le triangle MCD
M' est le milieu de DC
CM' et CH sont tangents au cercle de rayon 4cm de centreO
CH=CM'=MB=y
MH²=MO²-4²=(x-4)²-4²=x²-8x
mais MH=MC-CH=(x+y-6)-y=(x-6)
d'où
x²-8x=(x-6)²<=>4x=36
x=9cm
en reportant dans (3) on en déduit y=12cm donc AB=24cm
D.................M'................C
. .
. . .
O .
. .
. H .
. . .
. .
M..................B
merci pour cet exercice de géométrie
 Bonjour,
Bonjour,
Le rayon du cercle inscrit dans un triangle est
avec la surface du triangle et
les côtés.
Appelons la longueur du rectangle et
la largeur.
Ici, on a {i}
et {ii}
En extrayant des deux expressions, on trouve
qui équivaut finalement à
On en déduit en fonction de
et en remplaçant dans {i},
on obtient une équation du second degré d'où on tire et donc
Réponse à l'énigme: longueur du rectangle: 24 cm, largeur 9 cm.
Merci pour l'énigme.
A+, 
 Salut!
Salut!
La longueur du rectangle est de 24cm, sa largeur est de cm, soit environ 9.09cm en valeur approchée. Ma démonstration s'appuie sur les triangles semblables (ayant des rapports de longueurs égaux). J'ai fait un dessin avec ces longueurs trouvées et les 3 cercles sont bien tangents comme il faut, donc je pense que c'est correct (mais rien ne t'empêche de tuer ces souris jamo
 )
)
@+ et merci pour l'énigme!
 bonjour Jamo
bonjour Jamo
la longueur DC = 24
la largeur DA = 9
le triangle DAM est égal à la moitié du triangle DMC, ce qui permet de résoudre le problème dans un triangle rectangle unique ayant pour côtés la demi-longueur et la largeur du problème, ayant un cercle inscrit de 3 cm et un demi-cercle inscrit, dont le diamètre de 8 cm est compris entre le sommet de l'angle et un point du côté 'largeur'
soient ABC ce triangle rectangle en C, CB et CA étant respectivement la demi-longueur et la largeur du rectangle; I le centre du cercle inscrit et H sa projection sur [BC]; O le centre du demi-cercle inscrit de rayon 4 cm, O étant sur [AC]; J la projection de O sur [AB]
les points B, I, O sont alignés sur la bissectrice de l'angle ABC; les triangles BIH et BOC sont semblables et leur rapport de similitude = IH/OC = 3/4
BH/BC = 3/4; HC/BC = 1/4; BC = 4*HC = 4*3 = 12 -> longueur du rectangle = 24
les triangles rectangles AOJ et ABC sont semblables car ils ont un angle aigu commun en A; leur rapport de similitude = JO/BC = 4/12 = 1/3
soit x = OA
AB = 3OA = 3x
AB² = 9x² = BC²+AC² = BC²+(OC+OA)² = 12²+(4+x)² = 144+16+8x+x²
8x²-8x-160 = 0; x²-x-20 = 0; x = 5
AC = OC+AO = 4+5 = 9 -> largeur du rectangle = 9
 Bonjour à tous !
Bonjour à tous !
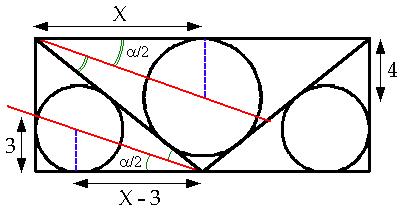
Voici ma solution :
Tout d'abord ces 3 cercles sont inscrits dans les 3 triangles, leur centre est donc situé à l'intersection des bissectrices.
Je prends ensuite  l'angle AMD (ou MDC ou MCD ou BMC) et
l'angle AMD (ou MDC ou MCD ou BMC) et  la longueur AM.
la longueur AM.
On déduit les équations suivantes :
tan ( /2)
/2) (
( -3)=3
-3)=3
tan ( /2)
/2)
 =4
=4
d'où :
tan ( /2)
/2) (
( -3)+1 = tan (
-3)+1 = tan ( /2)
/2)

<=> tan ( /2)=1/3
/2)=1/3
AM = 4/tan ( /2) = 12 cm
/2) = 12 cm
d'où: CD = 2 AM = 24 cm
AM = 24 cm
et: AD = AM * tan ( ) = 9 cm
) = 9 cm
Donc les dimensions du rectangle sont CD = 12 cm et AD = 9cm.
Voici le dessin qui va avec :
 Bonsoir
Bonsoir
En utilisant une méthode purement trigonometrique (que j'ai pas trop aimé d'ailleur) je trouve:
longueur = 24cm
largeur = 9cm
merci pour l'énigme  .
.
je developperai ma démo un peu plus tard
 Bonjour jamo
Bonjour jamo 
Petit rappel : si S est l'aire d'un triangle, p son demi-périmètre et r le rayon du cercle inscrit, on a la relation S = rp.
Soit a = AD la largeur du rectangle et 2b = AB sa longueur.
Dans le triangle ADM cette relation s'écrit :
Dans le triangle DCM, elle s'écrit :
On en déduit
d'où
Puis
Conclusion :
La largeur du triangle est égale à 9 cm, sa longueur est égale à 24 cm
Cordialement
Frenicle
 Bonjour
Bonjour
En voici ma démo:
La = L + d2 +3
or tg = (d1+3)/L ==> L = (d1+3)/tg
= (d1+3)/L ==> L = (d1+3)/tg et on a cos
et on a cos = d1/3 ==> d1=3cos
= d1/3 ==> d1=3cos
d'ou L= (3cos +3)/tg
+3)/tg
et on a d2 = 3sin on obtient donc La=(3cos
on obtient donc La=(3cos +3)/tg
+3)/tg + 3 sin
+ 3 sin + 3 = 3.(cos
+ 3 = 3.(cos +sin
+sin +1)/sin
+1)/sin (1)
(1)
on a tg = (Lo/2)/La =d/La ==> d = tg
= (Lo/2)/La =d/La ==> d = tg *La ==> d=3.(cos
*La ==> d=3.(cos +sin
+sin +1)/cos
+1)/cos (2)
(2)
D'autre part on a tg( /4 -
/4 -  /2) = 4/d ==> tg(
/2) = 4/d ==> tg( /4 -
/4 -  /2) . d = 4 (3)
/2) . d = 4 (3)
après quelques calculs trigonometrique je trouve tg( /4 -
/4 -  /2) = (1+cos
/2) = (1+cos -sin
-sin )/(1+cos
)/(1+cos +sin
+sin )
)
(3) donne donc 3.(1+cos -sin
-sin )/cos
)/cos = 4
= 4
on pose x=cos ==> sin
==> sin =
= 1-x² la résolution de l'équation si dessus est très simple ça donne x = cos
1-x² la résolution de l'équation si dessus est très simple ça donne x = cos = 3/5 , sin
= 3/5 , sin =4/5
=4/5
en remplacant dans (1) on obtient La=9cm et (2) donne d=12 cm==> Lo=24cm
désolé pour l'image manqué, j'ai pas pu l'insérer en totalité car ses dimensions depassent, mais bon la partie qui doit être vu est bien visible  .
.
 largeur : 24
largeur : 24
hauteur : 9
Appelons l la demi-largeur, h la hauteur
du fait de la symétrie de la configuration, le cercle de 4 centimètres est centré à l'intérieur du rectangle.
Son centre est à égale distance de [CD] et de [MC] (cette distance est le rayon du cercle : 4), donc il est sur la bissectrice. Soit l'angle que fait cette bissectrice avec [CD].
Cet angle est aussi celui que fait la bissectrice de avec [MB], sur laquelle est le centre du cercle de rayon 3.
Posons
Alors en appelant a=4, b=3 :
De ces équations, on obtient
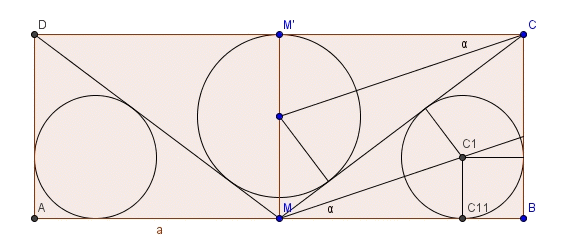
 Il y a plusieurs triangles rectangles dans la figure ci-dessous :
Il y a plusieurs triangles rectangles dans la figure ci-dessous :
DMH' et DMA
DH'O et DO'K'
MOH et MKO
On en déduit l'égalité des angles H'DO, O'DK', KMO et HMO
Si on pose x = AM, on a :
OH = 3, MH = x-3
O'H' = 4, DH' = x
DH'O' et MOH ont donc deux angles en commun donc les longeurs de leurs côtés respectifs sont proportionnels et on a :
x/4 = (x-3)/3
Ce qui donne x = 12
Ensuite, Tan H'DM = y/x
et l'angle H'DM est le double de l'angle H'DO'
d'où : Tan(2*Cotan(4/x)) = y/x
Ce qui nous donne y = 9
Puisque M est milieu de [AB] et que AM = x, on a AB = 2*x = 24
Le rectangle est large de 24 cm et haut de 9 cm.
 Bonjour,
Bonjour,
Longueur du rectangle: 24cm.
Largeur du rectangle : 9cm.
Sur la figure donnée :
Soit le point M' milieu de DC . Donc MM'//AD//BC.
Les triangles ADM,M'MD, M'MC et BCM sont égaux.
Soit le point S milieu de DM et par symétrie par rapport à ce point on construit le cercle de rayon 3cm dans le triangle M'MD.(on peut le construire par l' intersection des bissectrices du triangle M'MD)
La tangente au premier cercle //à AD est tangente au deuxième cercle.
DM' = 6+6= 12cm donc DC = 24cm.
La droite qui passe par les 2 centres des cercles donnés de 3cm sur la figure est tangente aux figures construites par symétrie donc AD = 6+3= 9cm.

Dimensions du rectangle
longueur 24cm
largeur cm
axe de symétrie de la figure  NM)
NM)
Considérons les triangles DAM et DAC
les cercles étant tangents aux cotés des triangles,sont inscrits dans les triangles et ont pour centre O1 et O2 , points de rencontre des trois bissectrices intérieures des triangles.
notation angle KDO1=(1/2)angle KDM=xet angle MDO2=(1/2 )angle MDN=y
angle HMO1=(1/2)angle HMD=(1/2angle )MDN puisque les angles HMD et MDH sont alternes-internes par rapport aux droites parallèles (DN) et (AM) et la sécante (DM)
par suite angle HMO1=y
Or l'angle ADN=90° donc x+y=45°
tanx=KO1/DK=3/(DA-3)
tan y=NO2/DN=4/DN
tany=HO1/HM=3/(AM-3)=3/(DN-3)
4/DN=3/(DN-3)===>4(DN-3)=3DN===>DN=12 et longueur du rectangle AB=2*12=24 cm
tany=4/12=1/3
tan(x+y)=tan45°=1
tan(x+y)= (tanx+tany)/(1-tan x*tany)
1=(3tanx+1)/(3-tanx)===> tanx=1/2
1/2=3/(DA-3)===>6=DA-3===>DA=9 largeur du rectangle 9 cm
 Posons:
Posons:
i l'angle (DCM),
N, le milieu de DC,
O, le projeté orthogonal sur (DC) de l'intersection du grand cercle avec la droite (CM),
P, le projeté orthogonal sur (AB) de l'intersection du petit cercle de droite avec la droite (CM),
R, le rayon du grand cercle,
r, le rayon des p'tits cercles,
L, la longueur du rectangle,
l, sa largeur.
On pose x = NO, y = PM.
La magie des équations triangulaires nous donne:
((L/2)-x)/(R.(1+cos i)) = tg i,
((L/2)-r-y)/(r.(1+cos i)) = tg i,
x = R.sin i,
y = r.sin i.
On obtient donc:
L = 2.R.(1+cos i)/sin i = 2.r.(1+cos i+sin i)/sin i
Soit:
(R-r).(1+cos i) = r.sin i
On pose:
K = (R-r)/r,
sin i = s
Cela nous donne:
cos²i = 1-s²
d'où:
K.(1+(1-s²)½) = s
K.(1-s²)½ = s-K
On élève au carré:
K².(1-s²) = s²-2.K.s+K²
(K²+1)s²-2.K.s = 0
s étant nécessairement différent de 0, on obtient:
s = 2.K/(K²+1)
Soit s = 3/5
On reprend:
L = 2.R.(1+(1-s²)½)/s = 2.R.(1+4/5)/(3/5) = 6.R
Or, R = 4cm, d'où L = 24cm
Calculons l:
l/(L/2) = (1-s²)½/s = 4/3
D'où:
l = 2.L/3
AN: l = 16cm
 Bonsoir,
Bonsoir,
bon, je me lance : le rectangle doit mesurer 24 de long et 9 de large.
J'ai utilisé les propriétés des cercles inscrits dans les triangles, et notamment le fait que le rayon = le double de la surface du triangle divisée par la somme des côtés.
Pour le cercle de rayon 3 j'ai considéré :
AM = b
AD = c
DM = a ou
La surface S du triangle ADM est alors égale à
Donc, première équation :
ou encore
Pour le cercle de rayon 4 j'ai considéré :
DC = 2b (car M est au milieu)
MC = a ou
DM = a ou
La surface S du triangle DMC est de toute façon le double de celle du triangle ADM
Donc, seconde équation :
ou encore
Après résolution des équations j'obtiens :
b = 12
c = 9
a = 15
Et donc un rectangle de 9 * 24.
 CB=9cm et DC=24cm
CB=9cm et DC=24cm
P sur MC tg au cercle(4), Q sur MC tg au cercle(3), N milieu de DC, NM coupe le cercle(4) en N'.
MB=x, BC=y
MC=(x-3)+(y-3)=x+y-6
MC=MP+x
donc MP=y-6
MP²=MN'*MN
donc (y-6)²=y*(y-8) => y=9
Aire MBC = x*y/2=3*(y-3)+3*(3-3)+3*3 avec y=9 => x=12
 pour commencer, on remarque que ce sont des cercles inscrits...
pour commencer, on remarque que ce sont des cercles inscrits...
Pour faciliter mes calculs, j'ai posé AM = x et BC = y
Une formule du cercle inscrit est r = 2S/(a+b+c) avec r le rayon du cercle inscrit, S la surface du triangle, et a b c les longueurs du triangle
Si on l'applique au triangle CDM
on a CD = 2x
et CM = DM =  (x2+y2) (Pythagore dans le triangle MBC...)
(x2+y2) (Pythagore dans le triangle MBC...)
et r = 4
et S = 2xy/2
donc 4 = 2xy/(2x+2 (x2+y2))
(x2+y2))
d'où  (x2+y2) = xy/4 - x
(x2+y2) = xy/4 - x
Pour le triangle MBC
on a MB = x, CB = y et CM =  (x2+y2)
(x2+y2)
r = 3
S = xy/2
donc 3 = 2xy/(2(x+y+ (x2+y2)))
(x2+y2)))
soit  (x2+y2) = xy/3 - x - y
(x2+y2) = xy/3 - x - y
DONC xy/4 - x = xy/3 - x - y
ce qui donne y(12-x) = 0
y 0
0
donc x = 12
on remplace ensuite le x dans l'une des égalités et on trouve y = 9
Longueur du rectangle : 24 cm
Largeur du rectangle : 9 cm
Epargne ces pauvres petites bêtes !!! ^^
 Soit AD=a, AM=b, DM=c, c^2=a^2+b^2, et en exprimant l'aire des triangles comme le produit du demi-périmètre par le rayon du cercle inscrit, il vient:
Soit AD=a, AM=b, DM=c, c^2=a^2+b^2, et en exprimant l'aire des triangles comme le produit du demi-périmètre par le rayon du cercle inscrit, il vient:
a*b=3(a+b+c)=4(b+c) d'où l'on déduit b+c=3a, donc b=12, c=3a-12 donc a=9.
Dans le rectangle, AD=9 et CD=24
 Bonjour,
Bonjour,
Les cercles sont inscrits aux triangles. Nommons comme mis sur la figure les pieds des hauteurs partant des centres des cercles, qui sont donc sur le cercle.
KR=KS=KT=3
JH=JU=4
Maintenant, exprimons l'aire du triangle HDM. Rectangle en H, on peut dire qu'elle est égale à (car HD=x/2)
Or,
====>
=> (1)
De la même manière, on a :
D'après (1) :
(x 4)
y différent de 0 (sinon, vive le problème ^^)
=> x = 24
On remplace tout simplement dans (1) et ça se simplifie très bien, pour donner y = 9 (je ne détaille pas celui-là, parce que j'ai beaucoup galéré pour texiser tout ça  )
)
 La longueur du rectangle est 24cm. Sa largeur est 9cm.
La longueur du rectangle est 24cm. Sa largeur est 9cm.
Pour arriver à ce résultat, j'ai superposé l'angle à l'angle
. (Le cercle de rayon 4cm a suivi).
Nous avons ainsi les deux cercles inscrits à l'angle .
Comme le lieu des centres des cercles inscrits à un angle est la bissectrice de cet angle et puisqu'on connait la position exacte des centres des deux cercles, on peut trouver la tangente de l'angle .
.
AM vaut donc .
Comme
AD vaut donc
Le rectangle fait donc bien 24cm par 9cm.
 bon je n'ai sans doute pas pris la méthode la plus simple...mais ca fonctionne...
bon je n'ai sans doute pas pris la méthode la plus simple...mais ca fonctionne...
j'ai considéré A comme centre du repère, D(0,h), et M (l/2,0)...
le cercle de rayon 3 a pour équation:
(x-3)²+(y-3)²=3²
et la droite BM a pour équation y=h-2h/l*x
sur l'intervalle qui nous intéresse l'équation de cercle peut s'écrire :y=3+(6x-x²)^(1/2)
Vu que DM est tangent au cercle de rayon 3, il n'y a qu'une seule solution à 3+(6x-x²)^(1/2)=h-2h/l*x
donc il faut que le discriminant s'annule.
d'où h=6*(l-6)/(l-12).
On réitère la même méthode avec un cercle rayon 4 (cf image jointe): (y-4)²+x²=4², et la même droite y=h-2h/l*x.
Le discriminant doit aussi s'annuler vu qu'il y a tangence.on trouve alors h=8l²/(l²-64)
on obtient alors une équation de degré 3:
8l²/(l²-64)= 6*(l-6)/(l-12) et on fait un tableau de variation avec étude de la dérivée pour trouver la solution:
on a alors l=24cm, et h=9cm
J'espère avoir été assez explicite et j'espère surtout ne pas avoir fait d'erreur...
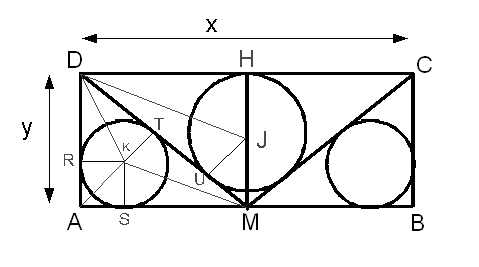
 Bonjour,
Bonjour,
Vu que les cercles inscrits se trouvent sur les bissectrices, on en déduit facilement quelques égalités de longueurs (voir dessin).
Il faut ensuite trouver x et y.
Avec les notations de mon dessin on a :
b2+z2 = (x-b)2
x2+y2 = (y+z)2
reste à déterminer z :
x-a + y-a = y+z
z = x-2a
d'où :
b2+(x-2a)2 = (x-b)2
x = 2a2 / (2a-b)
y = (x2-z2) / 2z
y = a.b / (b-a)
a = 3 cm
b = 4 cm
x = 9 cm
y = 12 cm
AB = 24 cm
AD = 9 cm
 Dsl pour l'indexation des equations du systeme je l'ai inversée.
Dsl pour l'indexation des equations du systeme je l'ai inversée.
L'equation (1) c'est celle en bas et (2) est celle en haut la solution reste la meme sans changement merci
Enfin voila la version finale de ma solution proposée:
 Définitions
Définitions
Le rectangle est nommé ABCD en partant en haut à droite et dans le sens des aiguilles d'une montre
E est le milieu du segment CD.
F est le milieu du segment AB
O est le centre du cercle central
P est le centre du cercle de droite
J est la projection orthogonale de P sur CD
N est la projection orthogonale de O sur EB
 est l'angle PEJ, moitié de l'angle CEB
est l'angle PEJ, moitié de l'angle CEB
s est le rayon du cercle central = 4cm
r est le rayon du cercle de droite = 3cm
Méthode :
Expression des segments en fonction de 
Elimination de 
Expression de EC en 
EC est égal à la moitié de la longueur
EC = EJ + JC
Le cercle étant tangent aux deux cotés du rectangle du sommet C, JC = r
Le triangle EJP est rectangle en J, aussi PJ = EJ * tan( )
)
PJ étant le rayon du cercle, PJ = r et EJ = r/tan( )
)
Ainsi
Expression de EF en 
EF est la largeur du rectangle
Nous appliquons le même calcul que précédamment au triangle ENO (rectangle en N)
L'angle EON est  , identique à PEJ
, identique à PEJ
EF = EO + OF = s/cos( ) + s
) + s
EF = (1 + 1/cos()) * s
Expression de EB en 
Nous appliquons le même calcul que précédemment au triangle ONB (rectangle en N)
L'angle NBO est aussi 
EB = EN + NB = s * tan( ) + s / tan(
) + s / tan( )
)
EB = (tan( ) + 1/tan(
) + 1/tan( )) * s
)) * s
Calcul de 
Nous appliquons la règle de trigonométrie sur le triangle OFB (rectangle en F)
L'angle FBO est 
OF = FB * tan( ) avec OF = s et FB = EC = (1 + 1/tan(
) avec OF = s et FB = EC = (1 + 1/tan( )) * r
)) * r
Ainsi
et
LONGUEUR rectangle : 2 * EC
En valeur numérique :
Calcul de la largeur : EF
Nous appliquons la régle de trigonométrie au triangle EFB (rectangle en F)
L'angle FBE est 2
FB est la moitié de la longueur du rectangle :
On a
Remplaçons par les valeurs précédemment calculées
.... FB est égal à EC précédemment calculé
[tex]LARGEUR = 2 * FB * \tan(2\alpha)
 Je n'ai pas pu mettre l'image avec, je vais donc décrire le découpage.On effectue le decoupage suivant:
Je n'ai pas pu mettre l'image avec, je vais donc décrire le découpage.On effectue le decoupage suivant:
W milieu de [DC].
O centre du cercle inscrit dans DMA, Q celui du cercle inscrit dans CBM et I celui du cercle inscrit dans DMC.
X sur [CB] tel que (QX)perpendiculaire(CB).
Y sur [AB] tel que (QY)perpendiculaire(AB).
Z sur [CM] tel que (QZ)perpendiculaire(CM).
V sur [CM] tel que (IV)perpendiculaire(CM).
U sur [DM] tel que (IU)perpendiculaire(DM).
Il est bon de noter qu'on a des cercles inscrits et que donc a posteriori, les points Q,O,I sont les points de rencontres des bissectrices (c'est à dire angle(WCI)=angle(ICM) etc...).
Notons ensuite les longueurs L et l tel que L=WC et l=CB.
On a alors les egalités suivantes:
Aire(CBM)=(l*L)/2=Aire(QXYB)+Aire(CZQX)+Aire(MZQY)=3*3+3*(l-3)+3*(L-3).
On a une première égalité:
(1) L*l=6*l+6*L-18.
On procède de la même facon dans DMC et on obtient:
Aire(DMC)=Aire(DCI)+Aire(MIC)+Aire(DIM)
Soit L*l=4*sqrt(l²+L²)+4*L.
On a une deuxième égalité:
(2) L²=(16*l)/(l-8)
En remplacant L par sa valeur en (1) on obtient une equation de degré 3 qui est:
20*l^3-312*l²+1476*l-2592=0
Elle a deux valeur complexe et une réelle qui est l=9.
Il vient alors la valeur de L qui est L=12.
Au final on a un rectangle de longueur 24cm et de largeur 9cm...
J'espère que les souris seront alors épargnées...
PS: Je m'excuse de devoir expliquer le découpage du rectangle au début, au lieu de mettre une image (plus parlante)... Mais je n'ai pas pu mettre cette image...
 Bonjour,
Bonjour,
DC = 24 cm et AD = 9 cm.
J'ai posé l'angle
, r le rayon de 3, R le rayon de 4 et P le projeté de M sur [DC].
Je me suis occupé du côté gauche (triangle ADM et cercle de rayon r) et j'ai trouvé ceci :
Ensuite je me suis occupé du côté droit (triangle DPM et du cercle de rayon R) et j'ai trouvé ceci :
ensuite, pour résoudre DP = AM ça fait mal ... donc j'ai approché la valeur de avec excel (résolution graphique) et j'ai regardé quelle valeur de AM ça donnait, comme on demande 'dimensions exactes' j'ai regardé si tout collait avec AM = 12 cm et oui !
 Bonjour,
Bonjour,
les dimensions du rectangle sont 24 x 9 cm
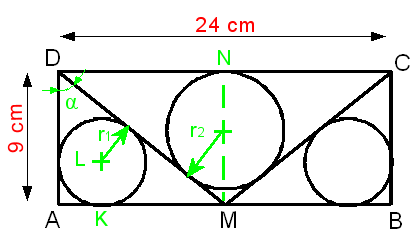
AD = r1 + r1.sin + (r1 + r1.cos
+ (r1 + r1.cos )/tan
)/tan = r1.[1 + sin
= r1.[1 + sin + (1 + cos
+ (1 + cos )/tan
)/tan ]
]
MN = r2 + r2.sin + (r2.cos
+ (r2.cos )/tan
)/tan = r2.[1 + sin
= r2.[1 + sin + cos
+ cos /tan
/tan ]
]
AM = tan .AD = r1.[tan
.AD = r1.[tan + tan
+ tan .sin
.sin + cos
+ cos + 1]
+ 1]
DN = tan .MN = r2.[tan
.MN = r2.[tan + tan
+ tan .sin
.sin + cos
+ cos ]
]
On pose X = tan + tan
+ tan .sin
.sin + cos
+ cos
AM = r1.(X + 1)
DN = r2.X
AM = DN  r1.(X + 1) = r2.X
r1.(X + 1) = r2.X  (X + 1)/X = r2/r1
(X + 1)/X = r2/r1
r1 = 3 ; r2 = 4 ; (X + 1)/X = 4/3 = (3 + 1)/3  X = 3
X = 3
On obtient = AM = DN = 3.(3 + 1) = 12 d'où la longueur du rectangle est égale à 24 cm
Soit  l'angle en M du triangle AMD, on a :
l'angle en M du triangle AMD, on a :
AD = tan .AM
.AM
tan = 2.tan(
= 2.tan( /2)/(1-tan²(
/2)/(1-tan²( /2))
/2))
tan( /2) = KL / KM = r1/(AM - r1) = 3/(12 - 3) = 1/3
/2) = KL / KM = r1/(AM - r1) = 3/(12 - 3) = 1/3
d'où tan = 3/4
= 3/4
d'où AD = 9 soit la hauteur du rectangle est de 9 cm
Merci et A+, KiKo21.
Nombre de participations : 0
Temps de réponse moyen : 94:57:32.