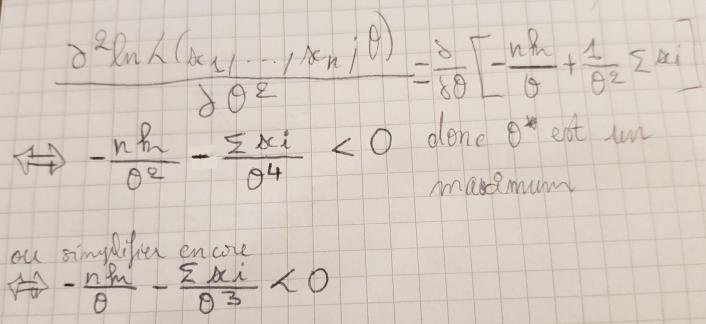Inscription / Connexion Nouveau Sujet
Estimation Ponctuelle / Maximum de Vraisemblance
**Bonjour**
On dispose d?un échantillon aléatoire (X1,...,Xn) de taille n d?une variable aléatoire X suivant une loi dont la fonction densité de probabilité s?écrit :
f(x;
) = P (X = x) = x
x
si x>0
sinon = 0
où est un paramètre réel positif, k un entier naturel non nul et 
une constante réelle. Le paramètre étant inconnue, on se propose de l?estimer ponctuellement.
-Déterminer la constante ? .
-Calculer la fonction de vraisemblance, de l?échantillon aléatoire au point d?observation (x1, · · · , xn).
-Déduire la log-vraisemblance associée à cette fonction de vraisemblance.
-Calculer l?estimateur du maximum de vraisemblance (EMV ) du paramètre .
-Cet estimateur est-il convergent ? Justifier.
-Cet estimateur est-il efficace ? Justifier.
-Quelle(s) autre(s) méthode(s) d?estimation ponctuelle peut-on proposer ?
-Calculer la moyenne théorique et la variance théorique de la variable aléatoire X
.
la FAQ du forum
moteur de recherche
page de choix du forum
fiches du siteBonjour j'ai essayé de répondre au sujet puis-je joindre des photos de mes brouillons dans la conversation ?
habituellement, non : 
Sujet ancien- ne plus donner ce lien-merci
en raison de la fin d'année perturbée, et à la condition expresse que ce soit propre comme le serait un devoir rédigé, oui pour aujourd'hui
Voilà la réponse que j'ai obtenue pour la question 1 :
Je vais mettre dans un autre commentaire celui de la question 2 et 3. Merci de votre compréhension.
malou edit > ** image autorisée** image tournée**tiens ton téléphone à 90°**
Hello !
Pas mal ln(0) = 1 !
Le lambda doit être choisi de sorte que f soit une densité de probabilité.
Dans quellle licence tu es?
Bonjour emeline97.
Pour que f soit une densité de probabilité il faut que
Comme dans ce cas f est nulle sur ]-
;0] on détermine avec la relation :
Voici ma réponse à la question 2 et 3.
Je suis en licence d'économie Lionel.
malou edit > * image autorisée*
Pour la question 4 je sais que je dois faire la dérivé 1er de la log de vraisemblance par rapport à téta est égale à zéro.
Pour la question 5 je dois faire la dérivée seconde de la log de vraisemblance par rapport à téta.
Mais je suis coincé à la question 4.
Je suis d'accord avec ton résultat à la question 3.
Pour dériver par rapport à , on se rappelle que la dérivée d'une somme est la somme des dérivées des termes de la somme.
Et que la dérivée d'une constante est nulle.
Les termes et
ont donc une dérivée nulle par rapport à
.
Il reste à dériver qui est de la forme
si on remplace
par x.
Merci pour votre réponse Verdurin. Je reviens vers vous avec ma dérivée ce soir ou demain matin. J'ai encore d'autres matières à voir !
Bonne soirée à vous tous, et merci pour votre aide .
Bonjour voilà ce que j'ai fais hier soir suite à l'aide de Verdurin pour la question 4, dites moi si il y a une erreur dans l'une des lignes. J'ai eu des hésitations mais au final voilà ce que j'ai trouvé !
malou edit > * image tournée*
Je suis d'accord jusqu'à
après le au dénominateur de la seconde fraction disparaît sans raison et la suite est fausse.
Petit rappel : un produit est nul si et seulement si un des facteurs est nul.
Pour continuer il faut mettre au même dénominateur ce qu'il y a dans les crochets puis regarder pour quelle valeur de le numérateur s'annule.
Je ne suis pas sur si c'est correcte mathématiquement :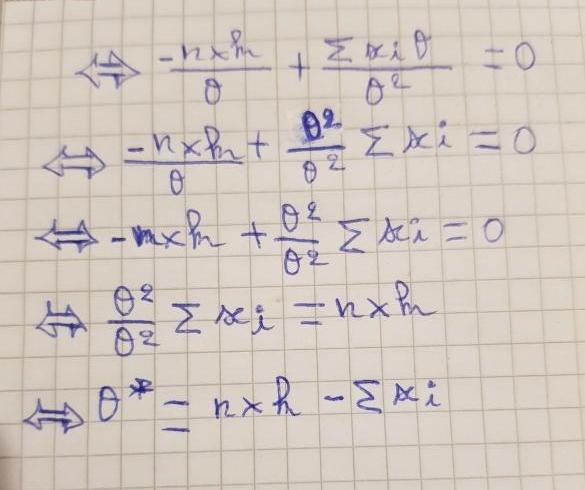
malou edit > * image à nouveau tournée, tiens ton téléphone à 90° comme déjà dit ! *
Voilà j'ai retourné l'image sur mon ordinateur car j'arrête pas de les prendre dans le mauvais sens !
Il y a une erreur que je n'avais pas vue.
La dérivée par rapport à de
est
.
Tu peux remarquer que dans ton calcul disparaît du numérateur ce qui revient à dire que la dérivée ne s'annule jamais et donc qu'il n'y a pas de maximum de vraisemblance en fonction des observations. Ce qui est très étonnant.
Reprends tes calculs à partir de
Bonjour emeline97.
Il y a encore des erreurs dans le calcul de la dérivée.
De façon générale quelque soit
( Sous réserve que la fonction soit définie. )
Ensuite il suffit de vérifier que la dérivée seconde est strictement négative en
Bonjour verdurin
je crois que je vais ajouter quelque part dans la FAQ que ce n'est pas parce qu'on se désinscrit, que le sujet disparaît....
Annuler
connectez vous