Inscription / Connexion Nouveau Sujet
Exercice math systémes d'inéquations
Le sujet :
Pour une réception de 40 personnes, il faut au minimum 5 petits fours, 2 glaces et 3 confiseries par personne.
Un pâtissier propose des assortiments A composés de : 50 petits fours, 8 glaces et 15 confiseries.
Un autre pâtissier propose des assortiments B composés de : 20 petits fours, 16 glaces, 20 confiseries.
On commande x assortiments A et y assortiments B.
1) Traduire les contraintes de la commande sous la forme d'un système d'inéquations portant sur x et y.
2) A tout couple ( x;y) de nombres réels, on associe le point M de coordonnées ( x;y)dans un repère orthonormé (0;i;j)
Résoudre graphiquement le système : x > 0
y > 0
5x + 2y > 20
x + 2y > 10
3x + 4y > 24
Hachure la partie du plan qui ne convient pas.
3) Le prix d'un assortiment A est de 40 euros, celui d'un assortiment B est de 60 euros.
a) Exprimer, en fonction de x et y, le coût C d'une commande.
b) Les couples (x;y) correspond à un coût C, sont les coordonnées des points d'une droite delta C dont on donnera une équation sous la forme y = ax+b.
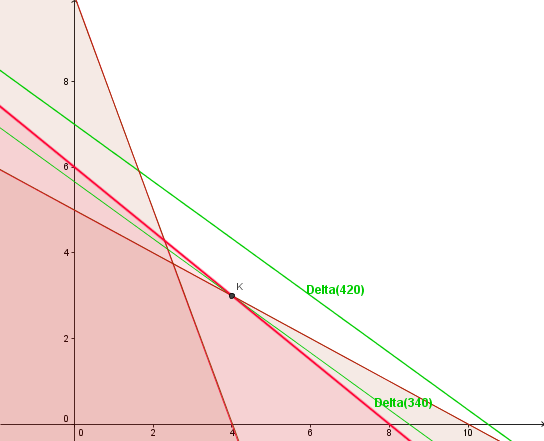
c) Tracer la droite delta 420, correspond au cas particulier où C = 420 euros.
4) Déterminer à l'aide du graphique le point par lequel doit passer la droite Delta C pour que le coût soit minimal.En déduire les nombre d'assortiments A et le nombre d'assortiments B correspondants. Calculer ce coût minimal.
Je pense avoir réussit l'exercice mais je n'arrive pas à trouver la question 4 car ma droite Delta 420 se trouve en dessous de toute mes autres droites donc dans la partie hachuré.Merci d'avance pour votre aide.
Bonjour Tweety,
La droite Delta(420), qui a pour équation 2x+3y = 420/20 , n'est pas "au-desous de toutes les autres" ; de toutes façons, cela n'aurait pas d'importance vu que la question 4 te demande de déterminer la droite Delta(C) d'équation 2x+3y = C/20 telle que C soit minimum tout en ayant au moins un point dans le domaine non hachuré : c'est la droite Delta C qui passe par le point d'intersection des deux droites de contrainte : 3x+4y = 24 et x+2y = 10 .
NB : tes > sont en fait des  ("il faut au minimum 5 petits fours, ...")
("il faut au minimum 5 petits fours, ...")
Bonjour,
Tout d'abord, pour le signe " > " je suis d'accord avec vous que c'est pas celui là, le probléme c'est que je suis nouvelle et je ne sais pas comment on fait le bon.
Pour ce qui est de savoir où se situe la droite est importante car nous devons trouver le point graphiquement et par pas un calcul comme le veux notre prof.
De plus,je ne comprend pas comment vous avez trouvé C/20.
Pour la question j'ai mis :
a) C = 40x+60y
b) 60y = - 40x + c
ce qui fait -2/3x + c/60
c) C = -2/3 x + 420/60 ce qui fait -2/3x + 7
Cette droite est en dessous des autres du coup le point recherché est dans la partie hachuré ce qui n'est pas possible.
1) Delta(420), d'équation 40x+60y = 420 soit encore y = 7-2/3x n'est pas "en dessous de toutes les droites de contrainte" (et même si elle l'était, ça n'aurait aucune importance, l'énoncé ne disant pas qu'elle passe dans la zone non hachurée).
2) La solution à la question 4) n'a rien à voir avec Delta(420), mais avec la droite parallèle qui passe par le point K, car elle correspond à la valeur minimum de C telle que Delta(C) ait encore au moins un point dans le domaine autorisé.
Jusqu'à preuve du contraire, les miennes sont celles de l'énoncé (du moins de l'énoncé que tu nous a donné).
Pour les droites le prof nous a dit de les résoudre par exemple :
5x + 2y > 20 SOIT 2y = -5x+20 soit y = -5/2x + 20, ce n'est pas comme cela ? Merci
1) 5x+2y=20 n'est pas équivalent à y = -5/2x + 20 mais à y = -5/2x + 10
2) Quoi qu'il en soit, l'équation 5x+2y=20 donne y=10 pour x=0 (point de la droite sur l'axe des ordonnées) et x=4 pour y=0 (point de la droite sur l'axe des abscisses) .
Ce que je ne comprend pas c'est pourquoi 5x+2y=20 n'est pas équivalent à y = -5/2x + 20 mais à y = -5/2x + 10.C'est le y = -5/2x + 10 que je ne comprend pas.


