Annuler
connectez vous
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Exercice type olympiade
Posté par Ahmat
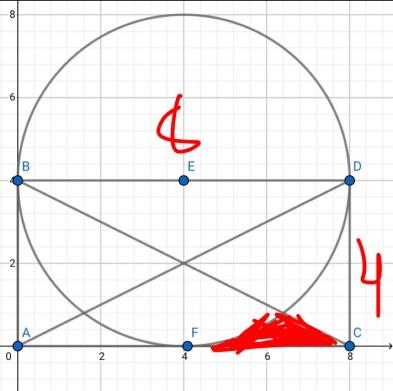
Bonjour mes chers amis passionnés de mathématiques. Notre professeur nous a donné un exercice pour les volontaires à chercher. Avec des collègues de ma classe nous avons dûment sans toutefois trouver. Alors je m'en remet à vous pour nous aider (solutions ou pistes peu importe). L'ennoncé est très simple : calculer l'aire en rouge de la figure ci jointe.
Bonjour,
déja ajouter des noms de points et au besoin le segment EF et quelques rayons utiles
ensuite on remarquera par exemple que
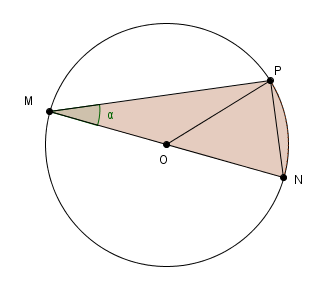
les triangles OMP et ONP ont même aire ...
ce qui permet de calculer l'aire curviligne MNP en fonction du rayon et de l'angle α
Je vous remercie pour votre réponse aussi rapide mais je n'ai pas trop compris la dernière partie de votre message. Pouvez-vous m'expliquer plus en détail ? Merci d'avance.
l'aire peinte de ma figure (figure précédente) est formée :
du secteur ONP, fraction d'un disque proportionnelle à l'angle au centre β
la formule est très simple si on exprime β en radians :
on vérifiera que si β = 2π on on obtient bien l'aire du disque entier (façon mnémotechnique de retenir cette formule)
plus l'aire du triangle OMP,
c'est à dire celle du triangle ONP dont l'aire se calcule avec une célèbre formule en sin β
aire d'un triangle etc par permutation circulaire
on est tout de même au niveau Terminale, et en olympiades même !
c'est à dire que un certain nombre de formules doivent venir immédiatement à l'esprit.
quel est le lien avec ce qu'on demande ?
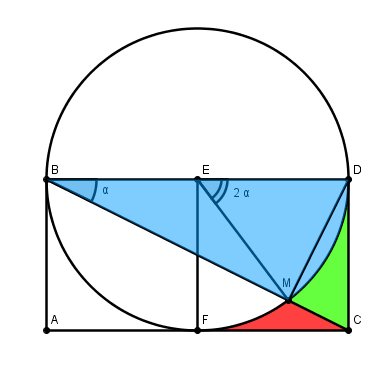
l'aire rouge demandée est obtenue par des sommes et différences d'aires dans cette figure :
même remarque pour les capacités d'imagination nécessaires pour des problèmes d'olympiade ... 
ce n'est certainement pas la seule façon de la calculer, mais c'est à mon avis l'une des plus simples.
Bonjour,
Autre méthode qui permet d'avoir immédiatement les lignes trigonométriques de et
et l'aire demandée:
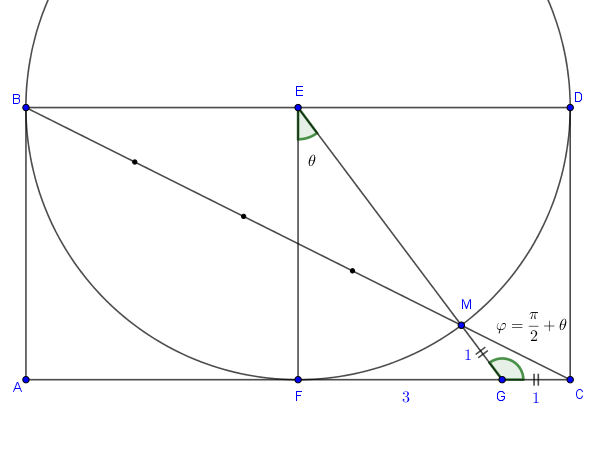
avec ma méthode mon angle avec tan(α) = 1/2 est encore plus instantané et on n'utilise que cet angle là (et son double) dans les calculs, qui ne sont de toute façon pas plus compliqués que ceux à partir de et
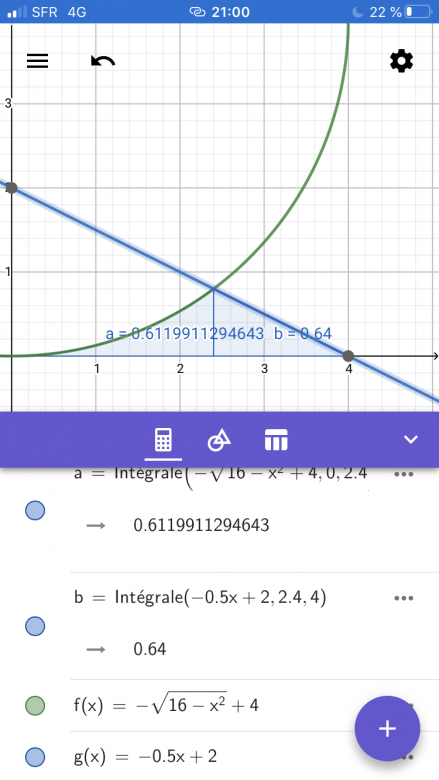
Il y a plusieurs façon de faire cet exercice, une que j'aime bien utilise les intégrales .
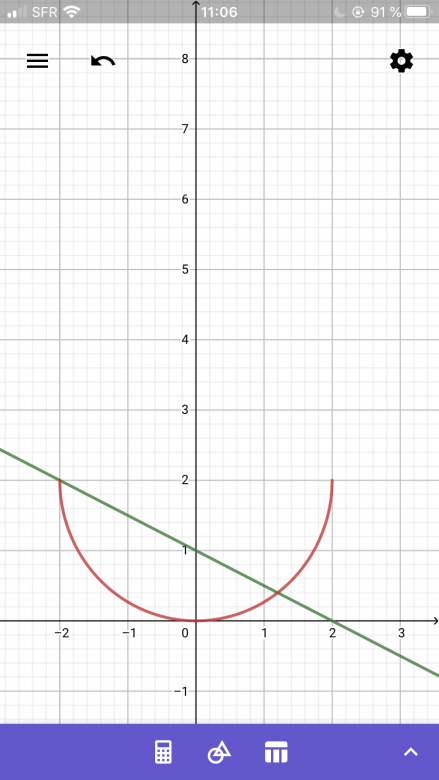
Le cercle a un rayon de 2 et on sait que :
Or on veut un demi cercle tourner vers le bas donc :
Ps : pour faciliter les calculs j'ai déplacé le cercle sur l'axe des ordonnées, et donc la droite également(voir image)
représente la droite qui coupe le cercle et dont on doit calculer l'aire en dessous à un moment.
On cherche donc le point d'intersection entre et
.
On a donc , le point d'intersection.
On peut donc faire l'aire d'un triangle rectangle en bas à droite. De côté :
L'aire est donc de 0.16 Unité d'aire.
L'autre aire consiste à résoudre cela :
Les bornes :
Et :
=
=
=
Si on connait la trigo :
On a :
On a donc :
=
=
=
On peut revenir plus loin dans x :
=
On aurait pu s'arrêter là mais :
Environ...
est l'aire en rouge total.
Environ, c'est une méthode un peu longue mais je l'aime bien.
Aie, j'avais pas fait gaffe, ton dessin est sur une unité de 2 au lieu de 1 mdr, super...
Mon unité d'aire est de 1*1, la tienne de 2*2,
1 carrée pour moi, 4 pour toi, sois l'aire :
De ton unité d'aire.
Autre méthode
Par un système à 4 équations
Les 4 inconnus sont le secteur rouge et les trois secteurs qui sont au voisinage.
On remarque que si on somme deux par deux on aura 4 équations.
Bonjour FerreSucrre,
J'ai l'impression qu'il y a quelque chose qui ne va pas.
La figure de 09h48 permet immédiatement d'avoir l'aire cherchée:
Soit environ .
Ne me demande pas où tu t'es planté...
Bonjour lake,
Citation :
La figure de 09h48 permet immédiatement d'avoir l'aire cherchée:
La figure de 09h48 permet immédiatement d'avoir l'aire cherchée:
il ne manque pas l'aire du triangle
Yes pirho je sais j'ai fais une rectification du calcul à la fin, j'ai fais comme si son 2j(vecteur) = J(vecteur)
2i(vecteur) = I (vecteur)
Donc à la fin j'ai multiplié par 4 mon résultat car il faut retourner sur du 1, donc 2*2, 4 carrée = 1 unité d'air pour moi, donc *4 = Son unité d'aire.
salut,
@FerreSucre
si tu veux que ton logiciel te donne un resultat exact, il faut entrer non 2.4 mais 12/5, non 0.5 mais 1/2
Est ce un logiciel de calcul formel ?
Bonsoir,
>>Pihro,
Je fais référence à ma figure de 09h48:
L'aire du triangle rectangle vaut
.
L'aire du secteur angulaire vaut
.
>>FerreSucre,
Citation :
Je maintiens mon résultat, après vérification il me semble que mon résultat est juste.
Je maintiens mon résultat, après vérification il me semble que mon résultat est juste.
Et moi, je maintiens le mien soit approximativement
Oui et Pihro l'avait bien vu: j'avais oublié le triangle .
Ce qui donne
Désolé d'avoir lourdement insisté