Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Bonjour à tous 
Un petit exercice rigolo :
Citation :
Soit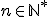 , déterminer tous les morphismes continus de
, déterminer tous les morphismes continus de ) dans
dans ) .
.
Soit
(exercice tombé à un oral d'Ulm)
Bonne chance, réponses en blanké svp.
Fractal

Bonjour,
 Cliquez pour afficher
Cliquez pour afficherApres y avoir réfléchit 2 minutes, l'ensemble des éléments d'ordre fini engendrant topologiquement S1, il suffit de regarder leur image par le dit morphisme, Il envoie donc un element d'ordre n sur une matrice diagonalisable dont le spectre est des racines n-ième de l'unité. Comme tout ce petit monde commute, on peut tous les diagonaliser dans une meme base. On se ramène donc à étudier les représentations de degré 1 du cercle.
Or un morphisme de S1 dans C^* c'est un morphisme de S1 dans S1, car sinon les elements se barrent vers 0 ou vers l'infini, ce qui ne vas pas car S1 est compact, donc son image aussi. Je posterai la suie quand j'ai le temps (si on connait un peu de théorie des representations, l'exo est facile.)
Or un morphisme de S1 dans C^* c'est un morphisme de S1 dans S1, car sinon les elements se barrent vers 0 ou vers l'infini, ce qui ne vas pas car S1 est compact, donc son image aussi. Je posterai la suie quand j'ai le temps (si on connait un peu de théorie des representations, l'exo est facile.)
Salut à tous
 Cliquez pour afficher
Cliquez pour afficherJe trouve que les morphismes continus de ce type sont de la forme =Pdiag(z^{k_1},z^{k_2},...z^{k_n})P^{-1}}) où les
où les 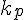 sont des entiers relatifs quelconques et P une matrice complexe inversible quelconque.
sont des entiers relatifs quelconques et P une matrice complexe inversible quelconque.
Voici comme j'ai abouti à ce résultat :
Tout d'abord, il est évident qu'une telle application définit un morphisme continu de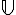 dans
dans })
On considère donc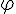 un tel morphisme.
un tel morphisme.
Tout d'abord, je commence par m'intéresser à l'image des complexes qui sont des racines de l'unité, c'est-à-dire aux complexes de la forme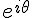 avec
avec 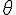 rationnel. Il existe donc un entier m tel que
rationnel. Il existe donc un entier m tel que 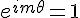 et donc, cela implique que
et donc, cela implique que ^m=I_n}) . En particulier, la matrice
. En particulier, la matrice }) est diagonalisable (car elle possède un polynôme annulateur scindé à racines simples).
est diagonalisable (car elle possède un polynôme annulateur scindé à racines simples).
Ainsi, toutes les matrices de la forme}) avec
avec 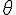 rationnel sont diagonalisables et leur valeurs propres sont des racines de l'unité (en particulier, elles sont de module 1).
rationnel sont diagonalisables et leur valeurs propres sont des racines de l'unité (en particulier, elles sont de module 1).
Par ailleurs, ces matrices commutent entre elles (car le groupe des complexes de module 1 est commutatif et donc son image par le morphisme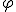 est un sous-groupe commutatif de
est un sous-groupe commutatif de }) ) donc ces matrices sont codiagonalisables et il existe donc une matrice inversible P tel pour tout rationnel
) donc ces matrices sont codiagonalisables et il existe donc une matrice inversible P tel pour tout rationnel 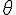 ,
, P}) est une matrice diagonale dont les coefficients diagonaux sont des complexes de module 1.
est une matrice diagonale dont les coefficients diagonaux sont des complexes de module 1.
Considérons maintenant un réel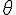 quelconque, alors il existe une suite de rationnels
quelconque, alors il existe une suite de rationnels }) qui converge vers
qui converge vers 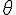 . Par continuité du morphisme
. Par continuité du morphisme 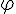 ,
,P}) converge vers
converge vers P}) et donc
et donc )}) converge vers
converge vers P}) . Cela entraîne donc que
. Cela entraîne donc que P}) est une matrice diagonale dont les coefficients diagonaux sont des complexes de module 1. Ainsi, il existe des fonctions
est une matrice diagonale dont les coefficients diagonaux sont des complexes de module 1. Ainsi, il existe des fonctions  définies sur
définies sur 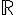 à valeurs dans
à valeurs dans 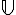 avec j compris entre 1 et n tel que pour tout réel
avec j compris entre 1 et n tel que pour tout réel 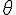 ,
, =Pdiag(\varphi_1(\theta),...,\varphi_n(\theta))P^{-1}}) . Comme P est inversible et que
. Comme P est inversible et que 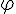 est un morphisme continu, alors les
est un morphisme continu, alors les  sont des morphismes continus de
sont des morphismes continus de 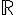 à valeurs dans
à valeurs dans 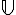 . De plus, ces n fonctions sont
. De plus, ces n fonctions sont 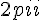 -périodiques. On va montrer que pour tout j, il existe un entier
-périodiques. On va montrer que pour tout j, il existe un entier 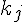 tel
tel =e^{i k_j \theta}}) , ce qui permettra de conclure.
, ce qui permettra de conclure.
On considère donc f un morphisme continu de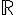 à valeurs dans le cercle unité complexe et
à valeurs dans le cercle unité complexe et 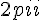 -périodiques. f est donc une fonction continue, non identiquement nulle et
-périodiques. f est donc une fonction continue, non identiquement nulle et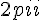 -périodique donc elle possède un coefficient de Fourier non nul et donc il existe un entier k tel que :
-périodique donc elle possède un coefficient de Fourier non nul et donc il existe un entier k tel que :
e^{-ik t}dt\neq 0})
Considérons l'intégrale=\Bigint_{0}^{2\pi}f(t)e^{-ik (t-\theta)}dt}) .
.
Tout d'abord, on a=e^{ik\theta}\Bigint_{0}^{2\pi}f(t)e^{-ikt}dt}) .
.
Par ailleurs, en effectuant le changement de variable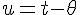 , on obtient :
, on obtient :
=\Bigint_{0}^{2\pi}f(u+\theta)e^{-iku}du=f(\theta)\Bigint_{-\theta}^{2\pi-\theta}f(u)e^{-iku}du=f(\theta)\Bigint_{0}^{2\pi}f(u)e^{-iku}du}) (car l'intégrale d'une fonction
(car l'intégrale d'une fonction 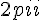 -périodique sur un intervalle de longueur de
-périodique sur un intervalle de longueur de 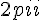 ne dépend pas de l'intervalle).
ne dépend pas de l'intervalle).
On a donc l'égalité\Bigint_{0}^{2\pi}f(u)e^{-iku}du=e^{ik\theta}\Bigint_{0}^{2\pi}f(t)e^{-ikt}dt}) pour tout réel
pour tout réel 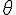 . Comme on a
. Comme on a e^{-ik t}dt\neq 0}) par hypothèse, alors on a
par hypothèse, alors on a =e^{ik\theta}}) , d'où le résultat.
, d'où le résultat.
Voici comme j'ai abouti à ce résultat :
Tout d'abord, il est évident qu'une telle application définit un morphisme continu de
On considère donc
Tout d'abord, je commence par m'intéresser à l'image des complexes qui sont des racines de l'unité, c'est-à-dire aux complexes de la forme
Ainsi, toutes les matrices de la forme
Par ailleurs, ces matrices commutent entre elles (car le groupe des complexes de module 1 est commutatif et donc son image par le morphisme
Considérons maintenant un réel
On considère donc f un morphisme continu de
Considérons l'intégrale
Tout d'abord, on a
Par ailleurs, en effectuant le changement de variable
On a donc l'égalité
Kaiser
Répondre à ce sujet
Un modérateur est susceptible de supprimer toute contribution qui ne serait pas en relation avec le thème de discussion abordé, la ligne éditoriale du site, ou qui serait contraire à la loi.Seuls les membres peuvent poster sur le forum !
Vous devez être connecté pour poster :
Connexion / Inscription Poster un nouveau sujet-
Ce topic
-
-
Fiches de maths
Menu
Espace membre
Changer d'île
-
Cours et Exercices de maths
- 6ème
- 5ème
- 4ème
- 3ème
- brevet
- seconde
- 1ère
- terminale
- bac
- post-bac
- bts
- capes
- Agregation
-
Outils de maths
- Calculatrice
- Calcul Crédit
- Tables de multiplication
- Tables d'additions
- Calcul de moyenne
- Addition de fractions
- Soustraction de fractions
- Produit de fractions
- Division de fractions
- Mise en fraction
- Inverse d'une fraction
- Puissance d'une fraction
- Partie entière d'une fraction
- Valeur décimale d'une fraction
-
Pages les plus populaires
- Théorême de Thalès et réciproque
- Trigonométrie et triangle rectangle
- Fonction exponentielle
- Cours sur les suites
- Exercices sur les suites
- Géométrie dans l'espace
- Produit scalaire
- Equation et mise en équation (Exos 4eme)
- Mise en équation (Exos 3eme)
- Probabilités
- Fonction Logarithme
- Equations différentielles
- Exercices calcul de pourcentages
- Formules dérivées
Mentions légales - Retrouvez cette page sur l'île des mathématiques
© digiSchool 2025


