Inscription / Connexion Nouveau Sujet
Factorisation
Bonjour, je poste ici car j'ai besoin d'aide pour une révision sur la factorisation pour mon boulot, j'ai une série d'expression à factoriser, et je ne m'en sors pas, forcément, 10 ans après la 3ème, on oubli vite..
Pourriez vous m'aider et m'indiquer les étapes de chaque expressions factoriser afin que je puisse comprendre? Merci d'avance
Voici les expressions: 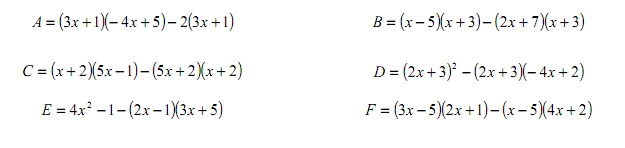

édit Océane : forum modifié
Je ne suis pas en maths sup, j'ai mis cela par erreur et d'ailleurs je ne sais pas comment modifier cela!
Tu devrais alors aller ici ![]() [lien]. L'on t'aidera sans problème !
[lien]. L'on t'aidera sans problème !
Cette île est immense !
A +
Bonjour, je poste ici car j'ai besoin d'aide pour une révision sur la factorisation pour mon boulot, j'ai une série d'expression à factoriser, et je ne m'en sors pas, forcément, 10 ans après la 3ème, on oubli vite..
Pourriez vous m'aider et m'indiquer les étapes de chaque expressions factoriser afin que je puisse comprendre? Merci d'avance
Voici les expressions: 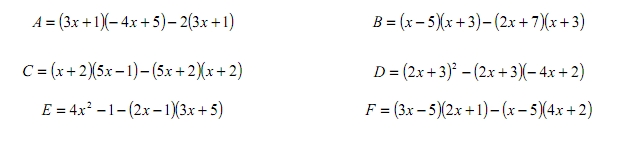

*** message déplacé ***
* Océane > le multi-post n'est pas toléré sur le forum ! *
J'ai posté, mais j'ai vraiment besoin d'aide pour ces expressions, je bloque énormément dessus et je ne suis pas très forte en maths, tout sa est a faire pour demain.. Je n'ai pas tous ce temps pour moi, je dois aussi m'occuper de mon fils ce soir.
Merci d'avance, c'est vraiment u-rgent
bonjour
le principe d'une factorisation est le suivant :
on sait que la multiplication est distributive sur l'addition et la soustraction...
autrement dit:
X (Y+Z) = X
(Y+Z) = X Y + X
Y + X Z
Z
X (Y-Z) = X
(Y-Z) = X Y - X
Y - X Z
Z
ces formules utlisées "dans l'autre sens" nous donnent des procédés pour catoriser:
si on a une somme et différences de produits et que dans chacun d'entre eux il y a un facteur commun (X dans la formule), alors on peut factoriser ce facteur commun et transformer la somme en produit
par exemple
A=(3x+1)(-4x+5)-2(3x+1) = (3x+1)[(-4x+5) - 2] = (3x+1)(-4x+5-2) = (3x+1)(-4x+3)
pour le D il faut se souvenir que (2x+3)²=(2x+3)(2x+3)
pour le E, une petite identité remarquable : X²-Y²=(X-Y)(X+Y) donc 4x²-1=(2x)²-1²=(2x-1)(2x+1)
pour le F on remarquera que (4x-2)=2(2x-1)
pour les deux derniers, il faut avoir l'oeil mais il me semble que ce sont des carrés arfait (identités remarquables : (X+Y)²=X²+2XY+Y²
et (X-Y)²=X²-2XY+Y²
bon courage et n'hésite pas à proposer tes solutions, je les corrigerai (une transformation par ligne, cela permet de repérer les erreurs éventuelles plus aisément)
mm
*** message déplacé ***
Merci pour cette aide et j'y vois plus claire pour le A, en revanche pour tout le reste, c'est le néant total...
Pour les deux derniers, j'ai compris le principe, mais la racine carré et le 1/4 me complique la raisonnement...
*** message déplacé ***
Pour le B, j'ai trouvé comme résultat (-x-12)(x+3) mais je doute que ce soit sa..
*** message déplacé ***
pour le B c'est correct
je pense que c'est bon mais il faut l'écrire correctement (mets les signes multipliés) : (x+2) (-3)
(-3)
tu vois que ce n'est pas si dur !
*** message déplacé ***
ou si tu ne mets pas le multiplié, mets des parenthèses (l'idéal c'est "les deux" !)
car si on lit (x+2)-3
ça fait
x+2-3
ou encore
x-1
et là c'est faux !
*** message déplacé ***
Merci beaucoup, mais pour le reste je ne comprend pas, et j'ai beau chercher, je n'y arrive pas
*** message déplacé ***
ben si, pour la D, avec ma remarque, essaye au moins de commencer (écris moi le détail)
*** message déplacé ***
(2x+3)²-(2x+3)(-4x+2)
(2x+3)(2x+3)-(2x+3)(-4x+2)
(2x+3) [(2x+3)-(2x+3)] (-4x+2)
(2x+3)(2x+3-2x-3)(-4x+2)
(2x+3)(-4x+2)
??
*** message déplacé ***
effectivement il y a un problème !
on ne garde que les deux premières lignes
tu as deux termes dans ta différence
chaque terme est un produit
et à chaque fois on retrouve le même facteur (2x+3)
dans le premier terme, ce facteur commun y est 2 fois ... mais une fois aurait suffit... donc on en factorise un des deux et on laisse l'autre !
Tu prends une seul fois le facteur (2x+3) dans chaque produit
c'est une structure XY - XZ = X(Y-Z)
avec X=2x+3
Y=2x+3
Z=-4x+2)
reprends à partir de la deuxième ligne
*** message déplacé ***
E = 4x²-1-(2x-1)(3x+5)
(2x-1)(2x+1)-(2x-1)(3x+5)
(2x-1)(2x+1)-(2x-1)(3x+5)
(2x-1)((2x+1)-3x+5))
(2x-1)(2x+1-3x-5)
(2x-1) (-x-4)
??
*** message déplacé ***
le E est bon... sauf qu'il manque une parenthèse ouvrante juste devant le "3x" à la quatrième ligne
*** message déplacé ***
D= (2x+3)²-(2x+3)(-4x+2)
(2x+3)(2x+3)-(2x+3)(-4x+2)
(2x+3) ((2x+3)-(-4x+2))
(2x+3) (2x+3+4x-2)
(2x+3)(6x+1)
*** message déplacé ***
Merci  Le F je viens d'essayer et les deux dernier aussi, mais je n'y arrive pas du tout...
Le F je viens d'essayer et les deux dernier aussi, mais je n'y arrive pas du tout...
Peux-tu me donner les étapes s'il te plait? car je ne comprend pas sur ces 3 là
*** message déplacé ***
essaye le F avec ma remarque de tout à l'heure (et continue à détailler)
ensuite je t'aiderai pour les deux identités remarquables
*** message déplacé ***
F = (3x-5)(2x+1)-(x-5)* 2(2x+1)
(2x+1)((3x-5)-(x-5))*2
(2x+1)(3x-5-x+5)*2
(2x+1)(2x)*2
??
*** message déplacé ***
c'est faux à partir de la deuxième ligne... le "*2" est "attaché au terme qui contient (x-5) et il n'est pas en facteur du tout...
F= (3x-5)*(2x+1) - (x-5)*2*(2x+1)
= (2x+1) [ (3x-5) - (x-5)*2 ]
continue
*** message déplacé ***
quand tu factorise, tu prélève UN facteur commun dans chaque produit... tu le mets en facteur pour tout le monde... et pour chaque produit, les autres facteurs restent en place
*** message déplacé ***
F= (3x-5)*(2x+1) - (x-5)*2*(2x+1)
= (2x+1) [ (3x-5) - (x-5)*2 ]
= (2x+1) ( 3x-5-2x+10 )
= (2x+1) (x+5)
??
*** message déplacé ***
pour les deux derniers c'est plus siouxe...
il faut repérer la structure (A+B)²=A²+2AB+B² pour la "C"
alors pour avoir A² = 2x² et B²=3, que faudrait-il prendre pour A et B ?
*** message déplacé ***
très bien
prenons A=( 2).x et B=
2).x et B= 3)
3)
(en appuyant sur le  en bas de la fenêtre de saisie, tu as des tas de symboles)
en bas de la fenêtre de saisie, tu as des tas de symboles)
et si on prend ces valeurs là, que vaut 2.A.B ?
*** message déplacé ***
je vais devoir quitter mais je reviens tout à l'heure...
essaye de voir si 2AB=( 24).x
24).x
*** message déplacé ***
Donc cela me fait ( 2+
2+ 3)² ?
3)² ? 
Merci beaucoup, il me manque plus que l'expression D 
*** message déplacé ***
Je me suis creusée pour le D et j'ai réussi  En tout cas merci beaucoup de ton aide et merci d'avoir pris le temps de m'aider et de me répondre!
En tout cas merci beaucoup de ton aide et merci d'avoir pris le temps de m'aider et de me répondre! 
*** message déplacé ***

 :?
:?

