Annuler
connectez vous
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
fonction
Posté par oumy1
Bonjour, en plus du DM le prof nous a envoyé 2 exercices. j'ai des difficultés pour les questions 4) et 5). Merci de bien vouloir m'aider.
Camille lance, à l'instant t=0, une balle de la fenêtre de sa chambre qui est à trois mètres du sol. on note h(t) la hauteur de la balle, en mètre, t secondes après avoir été lancée. on admet que la courbe représentative de la fonction h est une parabole de sommet S(2,5; 6,125).
1. déterminer sous forme canonique l'expression de h(t) en fonction de t.
2. développer et factoriser h(t).
3. pendant combien de temps la balle restera-t-elle au-dessus de 5 m de hauteur ?
4. la sœur de Camille, qui mesure 1,5 m, se trouve à 5,5 m de la maison. La balle l'atteindra-t-elle ?
5. si aucun obstacle ne se place sur la trajectoire de la balle, à quelle distance de la maison retombera-t-elle au sol ?
1)on a: la fenêtre est à 3m de hauteur.
S(2.5;6.125)
la forme canonique est: a(x-
)2 +
h(o)=3 alors je résous l'équation:
a(0+2.5)2+6.125=3
6.25a=3-6.125
a=
a=-0.5
La forme canonique de h(t) est: h(t)=-0.5(t-2.5)2+6.125
2)Développement de h(t)
h(t)=-0.5(t-2.5)2+6.125
=-0.5(t2-5t++6.125
=-0.5t2+2.5t+3
on calcule le discriminent pour la factorisation:
=12.25
>0 alors deux racines. t1=6 et t2=-1
donc h(t)= -0.5(t-6)(t+1)
3)On résous l'inéquation h(t)
5
-0.5t2+2.5t+35
-0.5t2+2.5t-20
=2.25 et
2.25=1.5
>0 donc 2 racines t1=4 et t2=1
La balle restera au dessus de 5 m de hauteur sur [1;4] donc 3 secondes
4)je ne sais pas comment faire.
5)je ne sais pas comment faire.
Merci d'avance de votre aide.
bonjour,
q4) cet énoncé contient une incohérence : l'axe des abscisses a tantôt une unité de temps, tantôt une unité de distance.
dans cette question, x = 5,5.
que vaut h(5,5) ? ca te dira à quelle hauteur passe la balle quand x=5,5..
est ce plus haut ou moins haut que 1,50 m ? autrement dit, la balle touchera-t-elle la soeur de Camille ou passera-t-elle au dessus ?
Bonsoir Leile etkenavo27 merci pour votre aide.
pour le 4) c'est bizarre pour l'axe des abscisses:
j'ai calculer : h(5.5) =-0.5(5.5-2.5)+6.125=1.625
Donc la balle n'atteindra pas la sœur de Camille qui mesure 1.50m.
pour le 5) graphiquement la balle retomberai au sol au bout de 6 secondes.
Pouvez vous me guider et m'aider merci.
bonjour,
q4) : ok
q5) la lecture graphique est insuffisante.
quand la balle est au sol, h(x) = 0. Utilise la question 2 pour résoudre..
(NB : pour cette question aussi, l'unité des abscisses est le mètre).
Cette incohérence dans l'énoncé existe depuis longtemps, mais ça n'a pas l'air de gêner puisque cet exercice continue d'être donné tel quel.
Bonjour Leilemerci de ton aide
si je prends la forme factorisée de h(t), h(t)=-0.5(t-6)(t+1)donc je conclus que c'est a 6 mètres de la maison que la balle arrivera au sol et non pas au bout de 6 secondes
AU SECOURS EST CELA???
oumy1
oui, on te demande à quelle distance, donc 6m. Tu peux préciser pourquoi tu ne retiens que la racine positive.
NB : inutile de crier au secours en majuscules 
Désolé Leile , je ne voulais pas être agressif,
il suffit donc d'expliquer pourquoi on ne prend que la racine positive. il n'y a aucun calcul.
j'aimerai savoir pourquoi cet exercice existe toujours puisqu'il est quelque peu absurde.
Merci pour ton aide
il y a quand même un calcul :
quand la balle retombe au sol, sa hauteur est à zero donc h(t)=0
soit -0.5(t-6)(t+1)=0
c'est une équation produit nul ==>
t-6 = 0 OU t+1 = 0
t=6 ou t =-1
et là, tu expliques pourquoi tu retiens t=6
pourquoi cet exercice existe toujours ? Je suis comme toi, j'aimerais savoir pourquoi..
Peut-être ton professeur aura un avis (pose lui la question si tu penses qu'il ne s'en sentira pas agressé !).
Bonjour,
pour montrer l'absurdité des questions 4 et 5 auxquelles on peut répondre absolument ce qu'on veut
une petite animation : 
lien Geogebra
on peut modifier la composante horizontale de la vitesse
deux copies d'écran avec des réglages différents de cette vitesse horizontale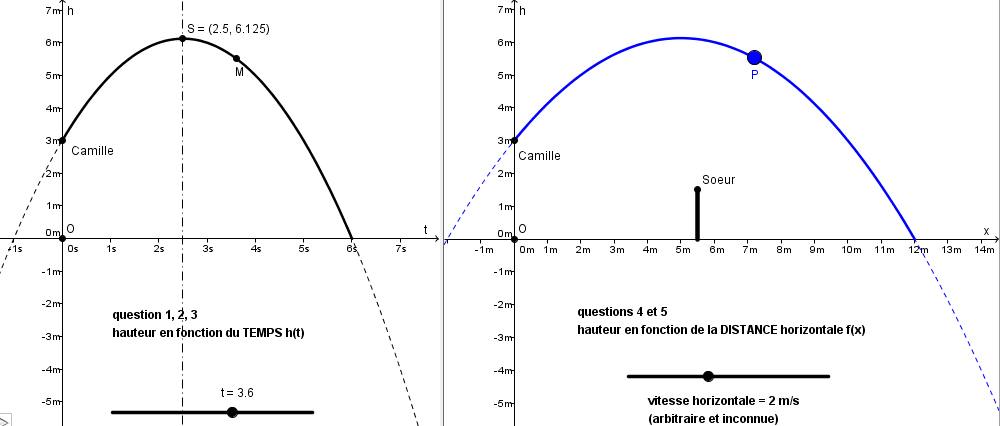
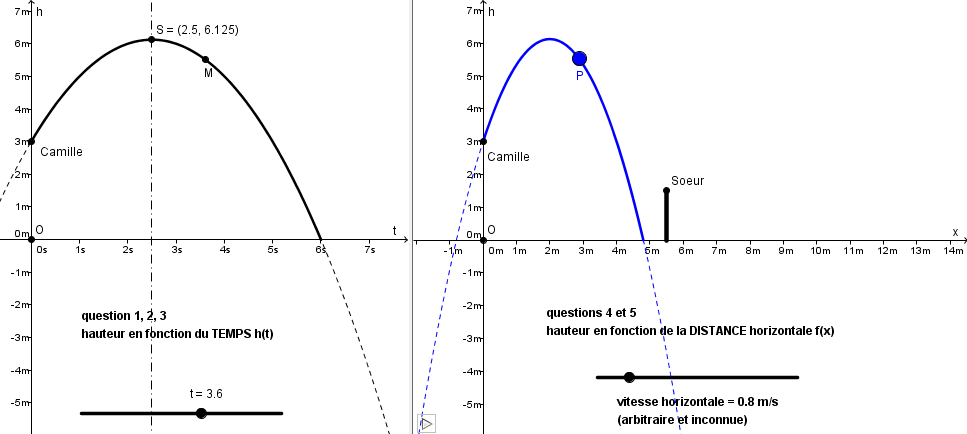
à transmettre au(x) prof(s) de maths concerné(s) pour qu'ils en parlent avec le prof de physique !
et corrigent enfin cet énoncé récurrent
(au lieu de se contenter de celui "du livre" qui est faux)