Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

fonction de transfert

Posté par
superpat 03-12-13 à 18:47

Bonjour,
Je suis nouveau sur ce site, j'aime le modélisme ''do it yourself'' et mon niveau en math n'est pas assez bon pour comprendre certaines fonctions.

Je dois m'intéresser aux filtres numériques pour filtrer les données lues d'un gyroscope.
Voici une fonction d'un filtre passe bas que je comprends (voir 1er fichier attaché)
avec y() la valeur de sortie x() la valeur d'entrée et a et b des coefficients

Mais je voulais comprendre comment calculer ces coefficients, et dans toute la littérature parlant de filtres numériques je tombe à chaque fois sur ce genre de formule (voir img2)

Je comprends que h(f) est la somme de tous les h(l) pour l variant de 0 à n-1 * par e qui est le logarithme népérien exposant -2PI * le nombre complexe j * la fréquence * la période d'échantillonnage .

Mais que représente numériquement  e^2PIjflTe pour pouvoir le représenter sur un graphique ?
Merci d'être indulgent dans vos réponses

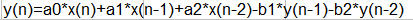
fonction de transfert

fonction de transfert

Posté par
kluxre : fonction de transfert 04-12-13 à 14:40

Bonjour,

e^{2\pi jflT_e}=\cos(2\pi flT_e)+j\sin(2\pi flT_e) : c'est donc l'affixe d'un point dans le plan complexe...

Posté par
superpatre : fonction de transfert 04-12-13 à 16:27

Bonjour,
la formule s'éclairci, merci.

Mais si c'est égal à cos(2PI*f*l*Te)+j*sin(2PI*f*l*Te) comment quantifier la valeur que cette réponse représente ?

Dois-je remplacer j par racine de -1 ?

=cos(2PI*f*l*Te)+ racine(-1)*sin(2PI*f*l*Te)

je mets tout au carré et je pose 2PI*f*l*Te = x

=cos²(x)- sin²(x)

comme cos²(x) + sin²(x) = 1 => sin²(x) = 1-cos²(x) => cos²(x) - sin²(x) = cos²(x) - (1-cos²(x)) = 2cos²(x) - 1

donc ma formule devient : 2cos²(2PI*f*l*Te) - 1

J'ai du me planter quelque part ?

Posté par
kluxre : fonction de transfert 04-12-13 à 16:51

J'ai parlé d'affixe.

C'est équivalent à parler de coordonnées.

M a pour affixe a+jb est équivalent à dire que M a pour coordonnées (a;b).

Ne t'embête donc pas avec ce j si tu veux représenter cela graphiquement.

Un point qui a pour affixe e^{2\pi jflT_e} est un point qui a pour coordonnées (\cos(2\pi flT_e);\sin(2\pi flT_e)).

Est-ce plus clair ?

Posté par
superpatre : fonction de transfert 04-12-13 à 17:06

Ca c'est vraiment beaucoup plus clair.

si je comprends bien, comme 2PI = 0° et/ou 360° si f=0 l=0 et Te=0
mon point se trouve aux coordonnées cos(0°) et sin(0°) ? soit 1 sur l'axe des x et 0 sur l'axe des Y ?

Mais dans ce cas, que vaut mon H(f) dans ma formule de départ ?
Il ne représente pas une valeur mais représente un point de coordonnées x et y à une fréquence f ?

Merci

Posté par
kluxre : fonction de transfert 04-12-13 à 17:15

Citation :
si je comprends bien, comme 2PI = 0° et/ou 360° si f=0 l=0 et Te=0
mon point se trouve aux coordonnées cos(0°) et sin(0°) ? soit 1 sur l'axe des x et 0 sur l'axe des Y ?


C'est bien ça

Mais dans ce cas, que vaut mon H(f) dans ma formule de départ ? \\ Il ne représente pas une valeur mais représente un point de coordonnées x et y à une fréquence f ?

H(f) représente bien une valeur, mais une valeur complexe.

Et, comme tout complexe, on peut le voir comme un point avec une abscisse et une ordonnée.

Il est courant d'utiliser les complexes pour faire des calculs en électronique (on peut sommer facilement des grandeurs).

Sauf que ce qui nous intéresse, ce sont des grandeurs réelles (et non pas complexes).

Pour un filtre, lorsque qu'on parle de fonction de transfert, c'est son gain G = |H(f)| (module de H(f)) et sa phase = arg(H(f)) (argument de H(f)) qui nous intéresse.

Une représentation graphique de H(f) n'a donc aucun sens physique.

Ce qui a un sens, par contre, c'est de tracer le gain G en fonction de f (ou de log(f), le logarithme décimal de la fréquence) et la phase   en fonction de f (ou de log(f).

C'est ce qu'on appelle un diagramme de Bode. Je ne sais pas si tu en as déjà entendu parler...

Posté par
superpatre : fonction de transfert 04-12-13 à 17:35

C'est vraiment super, j'ai bien compris le sens qu'il faut donner à H(f).

J'ai déjà vu des diagrammes de bode, mais je dois avouer que je cale sur les formules.
J'aimerais encore profiter de ces questions pour en revenir à mon filtre passe bas:
j'ai calculé mon filtre suivant ma formule ci-dessus y(n)=a0*x(n) ..... (img1A.jpg)
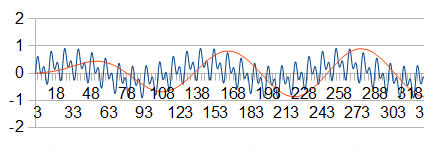
Il a l'air de répondre convenablement aux fréquences voulues:
Fréquence d'échantillonnage : 1000 Hz
Fréquence de coupure : 5 Hz
Facteur de qualité : 3

Que me faut-il pour tracer ce diagramme de bode ?

fonction de transfert

Posté par
kluxre : fonction de transfert 04-12-13 à 17:40

Rien de très compliqué, ne t'inquiète pas

(1) Calcule (puis trace) le gain G(f) = 20log(|H(f)|). Il suffit de calculer le module de H(f). Ensuite, tu prends 20log du résultat.

(2) Calcule (puis trace) la phase (f) = arg(H(f)). Il suffit de calculer un argument de H(f).

Posté par
superpatre : fonction de transfert 04-12-13 à 17:49

Ouppps

Tu vois je cale encore un peu
ce que j'ai c'est toutes les coordonnées (x,y) de mon signal filtré (en rouge)
x est donc mon module et y mon argument ?

Et si c'est correct, mes ordonnées sont en db et mes abscisses en Hz ?

Posté par
kluxre : fonction de transfert 04-12-13 à 17:55

Par définition, la fonction de transfert est le rapport entre la sortie et l'entrée : H = \dfrac{s}{e}. Ta courbe doit donc correspondre à |s| = |H||e| (je présume...).

Mais avec ta formule H(f)=\dfrac{1}{n}\dfrac{\sin(2\pi f n T_e/2)}{\sin(2\pi f T_e/2}e^{-2\pi j f (n-1)T_e/2}, tu peux calculer le gain (en calculant le module) et la phase (en calculant un argument). Non ?

Posté par
superpatre : fonction de transfert 04-12-13 à 18:49

La fonction de transfert H(f) était un exemple pour que je puisse bien comprendre ce fameux logarithme e exposant 2PIflTe
Et je crois avoir bien compris la façon de calculer un module et un argument.

Mais pour comprendre mon filtre, je vais devoir détailler ce que j'ai trouvé sur le net pour pouvoir le calculer.
Ce site est http://www.earlevel.com/main/2011/01/02/biquad-formulas/ et est vraiment super.

j'ai donc générer un signal quelconque sur excel (open office) qui représente la somme de 3 sinusoïdes de 100 50 et 30Hz (trace bleue).
Ma formule pour mon filtre est y(n)=a0*x(n)+a1*x(n-1)+a2*x(n-2)-b1*y(n-1)-b2*y(n-2) qui donne ma trace en rouge.
Pour une fréquence de coupure de 10Hz je dois d'abord calculer 2 valeur communes:

K=tan(PI*fc/fe) avec fe=1000Hz et fc=10Hz
L=1/(1+(K/Q)+K²) avec Q qui est le facteur de qualité.

mes coefficient pour ce passe bas sont :
a0 = K²*L
a1 = 2*a0
a2 = a0
b1 = 2*(K²-1)*L
b2 = (1-(K/Q)+K²)*L

Suivant les coefficients, il pourrait s'agir d'un passe haut, passe bande, etc ..
Est ce qu'avec ces données, je peux tracer le diagramme de bode ?

Posté par
kluxre : fonction de transfert 04-12-13 à 19:57

Qu'appelles-tu formule de ton filtre ? y est la sortie et x l'entrée ?

Désolé, mais j'ai de sérieux problèmes de connexion...

Je te conseille d'aller exposer ton problème sur forum.prepas.org dans la section Physique. Tu tomberas sûrement sur des personnes plus spécialistes.

Posté par
superpatre : fonction de transfert 04-12-13 à 20:09

C'est exact, x(n) est l'entrée et y(n) est la sortie.
C'est un filtre biquad

A chaque point x (signal d'entrée venant d'un gyroscope) j'obtiens le signal y représentant mon signal filtré à 10Hz.

Et j'aimerais visualiser la réponse en fréquence de ce filtre.

Je vais me diriger vers le site que tu me proposes.

Je te remercie vraiment pour le temps passé ensemble qui m'a fait comprendre cette fonction de transfert.
Cette convivialité n'est pas toujours identique sur d'autres sites surtout quand le niveau est bien supérieur au mien.

Merci beaucoup

Patrick

Posté par
kluxre : fonction de transfert 04-12-13 à 20:15

Je t'en prie

Je suis actuellement en dernière année d'école d'ingénieurs et mes connaissances sur les filtres remontent à ma prépa.

Je n'ai pas le temps de me plonger dans ton lien ce soir et mes problèmes de connexions n'aident pas...

J'espère que tu trouveras la réponse à ta question sur le forum que je t'ai conseillé. Il y a des professeurs de prépa et des ingénieurs qui répondent, donc il ne devrait pas y avoir de souci.

Si jamais tu n'obtiens pas ta réponse, j'essaierai de me plonger là-dedans.

Bonne recherche.

Posté par
kluxre : fonction de transfert 04-12-13 à 20:33

Je viens de trouver que la fonction de transfert pour un filtre Biquad est :

H(z) = \dfrac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}.

Avec z=e^{2\pi j f}, on se ramène à une fonction de transfert complexe (je ne connaissais pas la transformée en Z !).

Donc après on peut calculer le gain et la phase comme je l'expliquais plus haut.

Posté par
kluxre : fonction de transfert 04-12-13 à 20:42

z=e^{2\pi jT_e f} pardon.

Posté par
kluxre : fonction de transfert 04-12-13 à 20:48

Je suis tombé sur ces documents :

- , , (pour la fonction de transfert d'un filtre Biquad et la transformée en Z) ;

- (page 6 pour le diagramme de Bode).

Posté par
superpatre : fonction de transfert 05-12-13 à 16:47

Bonjour,
Merci beaucoup pour ces références.
Surtout http://www.louis-armand.uha.fr/btsSE/acrobat-modules/filnum.pdf
où il y a des exemples avec les solutions
Je préfère les exemples à la théorie.

Je cherche encore comment passe-t-on de

y(n)=a0*x(n)+a1*x(n-1)+a2*x(n-2)-b1*y(n-1)-b2*y(n-2)

à

H(z) = (a0 + a1 z-1 + a2 z-2) / (1 + b1 z-1 + b2 z-2)

je reviendrai vers vous de temps en temps pour de petites questions

Merci encore

Posté par
kluxre : fonction de transfert 05-12-13 à 18:06

H(z) = \dfrac{a_0+a_1z^{-1}+a_2z^{-2}}{1+b_1z^{-1}+b_2z^{-2}}=\dfrac{y(z)}{x(z)}

donc y(z)+b_1y(z^{-1})+b_2y(z^{-2})=a_0x(z)+a_1x(z^{-1})+a_2(z^{-2}).

On utilise ensuite le transformée inverse de Z (similaire à la transformée inverse de Laplace) :

y(n)+b_1y(n-1)+b_2y(n-2)=a_0x(n)+a_1x(n-1)+a_2x(n-2).

Posté par
superpatre : fonction de transfert 05-12-13 à 20:08

ouppps
le produit des extrêmes par le produit des moyens ...
Bon, je crois avoir assimilé la transformée en Z.
Reste le diagramme de Bode pour mon filtre.
J'ai regardé sur le net, et j'ai trouvé cette formule
Je vais essayer de l'appliquer à mon signal de sortie.
Patrick

fonction de transfert

Posté par
kluxre : fonction de transfert 05-12-13 à 20:13

Ces deux formules donnant le gain et la phase de déduisent directement de la formule de la fonction de transfert que tu avais donnée plus haut :

H(f)=\dfrac{1}{n}\dfrac{\sin(2\pi f n T_e/2)}{\sin(2\pi f T_e/2}e^{-2\pi j f (n-1)T_e/2}.

Posté par
kluxre : fonction de transfert 05-12-13 à 20:15

G(f)=20\log(|H(f)|) et \varphi(f)=\text{Arg}(H(f)).


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1760 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !