- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Fonction dérivée
Bonjour, quelqu'un pourrais m'aider et m'expliquer pour l'exo suivant ?
Partie A - Étude d'une fonction.
On considère la fonction f définie et dérivable sur l'intervalle [0;120] d'expression: f(x)=10/20+x.
Soit C sa courbe représentative dans un repère donné.
On admet que la fonction dérivée de la fonction f sur [0;120] est définie par f'(x)=-10/(20+x)².
1) Après avoir déterminé le signe de f'(x), dresser le tableau de variations de la fonction f sur l'intervalle [0;120].
2) Déterminer une équation de la tangente T à la courbe C au point d'abscisse 0.
Partie B - Application.
On réalise des expériences dans lesquelles une quantité de 1dm3 de substrat se transforme en un produit, sous l'action d'une enzyme.
On admet que la vitesse d'apparition du produit en µmol.s-1, en fonction de la concentration x, exprimée en mmol, peut-être modélisée par la fonction f définie à la partie A. Une représentation graphique de la fonction f est donnée sur la feuille annexe à rendre avec la copie.
1)En laissant apparents les traits de construction, déterminer graphiquement la vitesse de réaction pour une concentration de 15 mmol.
2) En laissant apparents les traits de construction, déterminer graphiquement pour quelle concentration la vitesse d'apparition du produit aura diminuée de 60%.
Je n'arrive pas à déterminé le signe de f'(x).
Pour le tableau je sais que (20+x)2 > 0 car il est au carré.
Mais après je bloque.
Le numérateur est négatif car il y a un moins devant 10.
Mais pour le mettre dans le tableau il faut que je face une équation ?
le numérateur est toujours négatif , le dénominateur toujours positif
donc est toujours
sur
Pourquoi faire un tableau ? et quelle équation voulez-vous résoudre
pas besoin d'équation ici.
on te demande quel est le signe de la dérivée :
le numérateur est toujours négatif, le dénominateur est toujours positif
--> le quotient (la dérivée) est toujours négative.
==> quel est donc le sens de variation de f ?
regarde dans les exemples du cours comment construire ton tableau de variation pour y consigner tes réponses
Pour ce qui est de la question 2 j'ai fait ceci :
T : y = f'(x0)(x - x0) + f(x0)
y = f'(0)(x - 0) + f(0)
y = -0,025 (x - 0) + 1/2
y = -0,025x + 1/2
Est-ce cela ?


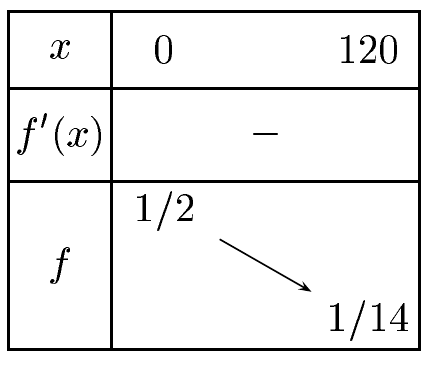 sans le ?
sans le ?
