- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
fonction dérivée
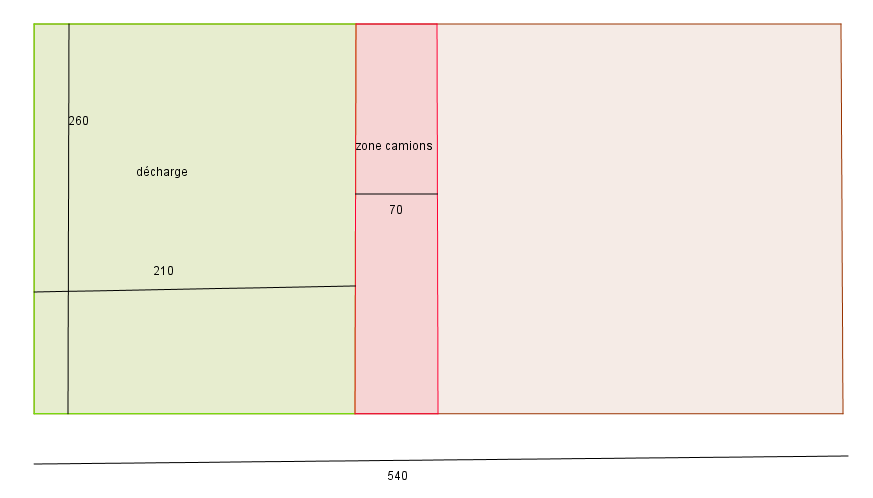
Bonjour je n'arrive pas à résoudre le probleme suivant : une commune désire implanter un centre de tri de déchets de chantier de forme rectangulaire à côté d'une décharge.
Le terrainn fait 540 m de long sur 260 m de large. La décharge fait 210 m de long, la zone camions 70m, le centre de tri est L. La commune a besoin d'un centre de tri de 23000m carré. Il faut déterminer la mesure de la côte x. sI X+25
1) calculer la largeur l du centre de tri.
2) calculer la longueur L du centre de tri
3) calculer l'aire du centre de tri
Puis en fonction de x : il faut calculer la largeur l du centre de tri puis calculer la longueur L puis montrer que l'aire A(x) est donné par la relation A(x) = 2x au carré - 780x + 67600
Merci de votre aide, je n'en peux plus...
Bonjour
N'y a-t-il pas un dessin joint au problème ?
Quelle largeur la décharge ?
Que veut dire le centre de tri est L ?
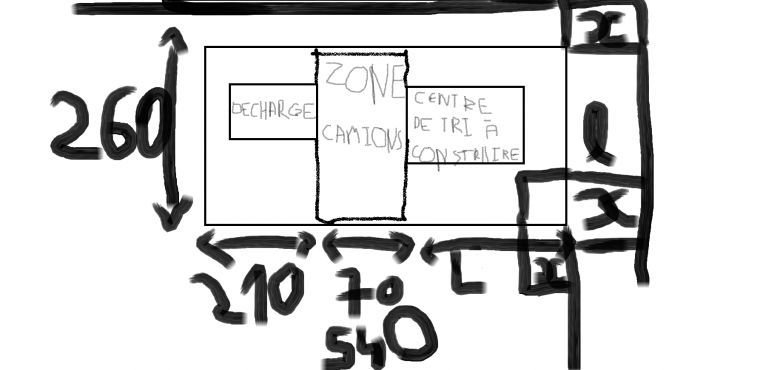
Oui il y a un schéma la largeur est 260m.la longueur de la décharge est de 260m puis au milieu la zone camions qui fait 700 puis le centre de tri qui est marqué par L puis la zone X. LA longueur totale fait 500M. J'espère être assez clair. Merci de votre aide.
Bonjour
l'ésotérique "faq 5" veut dire la question 5 de la Foire Aux Questions
FAQ dont le lien est donné dans le message ![]() Sujet ancien- ne plus donner ce lien-merci (qui est à lire avant de poster !!)
Sujet ancien- ne plus donner ce lien-merci (qui est à lire avant de poster !!)
et se trouve aussi dans le bandeau supérieur :
on ne te demandait pas de refaire un schéma quasiment à la main avec tes doigts sur l'écran tactile, mais de fournir le schéma d'origine, simplement cadré sur le seul schéma (ni le texte, ni la page entière, ni le bureau, ni le reste de la pièce, rien que le schéma)
vu que ce que tu as gribouillé dessus est quasiment incompréhensible
et contradictoire avec le texte donné avant lui même contradictoire avec le premier message :
au milieu la zone camions qui fait 700
et je lis 70
la longueur totale fait 500M
et je lis 540
alors qui a raison ???
avec un tel schéma c'est encore pire que sans !
et le texte doit être recopié mot à mot au caractère près et pas raconté à ta sauce.
ce que tu as dit dans le premier message est totalement incompréhensible
on espérait que le schéma aurait jeté une lueur là dessus, c'est encore pire avec ton bidouillis !
ce que j'ai compris
mais où se trouve le centre de tri
à quoi correspond l L et x et dans votre texte x+25
Bonsoir, voici mon problème : on considère la fonction f définie sur l'intervalle [0,220] par: A(x) = 2x au carré - 780x + 67600
1) calculer f'(x) où f' est la fonction dérivée de la fonction f
2) résoudre f'(x) = 0
3) compléter le tableau de variation : 0 ......... 220
signe f'(x) .....................................
sens de variation
de f(x) .........................................
Merci pour votre aide
Bonne soirée
*** message déplacé ***
ça serait tellement plus simple avec
une recopie mot à mot du texte exact de l'énoncé
et une photo du véritable schéma de l'énoncé tel qu'il est
parce que là je sens qu'on va tourner en rond éternellement...
voici ma réponse : 1)f'(x) = 2 x 2 = 4 = 2 divisé par 4 = 0.5
2) f'(x) = 0
2x au carré - 780x +67600 = 0
4x - 780x = 67600
x=67600 divisé par 780 = 86.66
Ai-je raison?
Merci
*** message déplacé ***
tu fais du multipost : c'est interdit sur ce site.
Je ne peux, ni ne veux, te répondre ici.
Continue sur ton premier post, où tu as déjà eu de l'aide. .
*** message déplacé ***
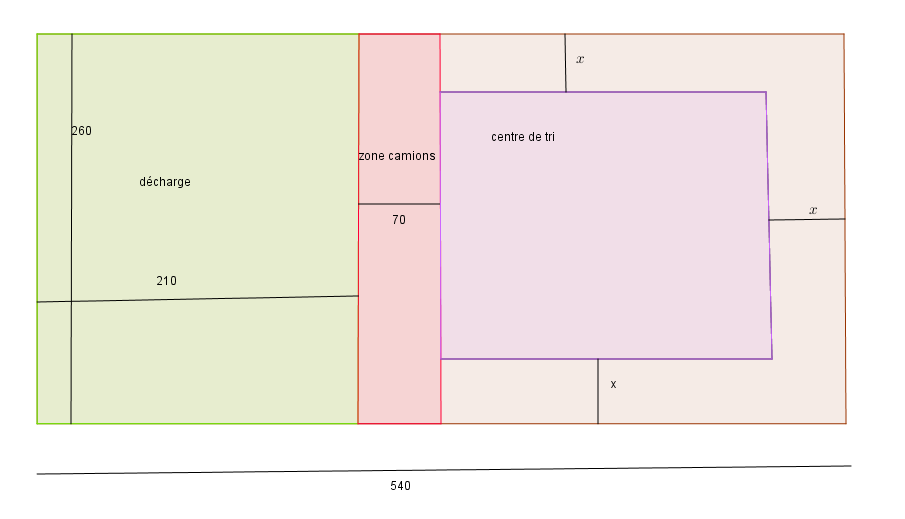
Bonsoir, oui je sais je me suis trompée sur le premier post (manque d'habitude sur le site).Le schéma pas très réussi contient les bonnes données. Le centre de tri est sur la droite de votre schéma dont on ne connait pas la longuer avec x juste à côté. La longueur totale est bien de 540.
1) on prend x=25. a) calculer la largeur l du centre de tri
b) calculer la longueur L du centre de tri
c) calculer l'aire du centre de tri
2) exprimer en fonction de x : a) la largeur l du centre de tri
b) la longuer L du centre de tri
c) montrer alors que l'aire A(x) du centre de tri est donné par la relation :
A(x) = 2x au carré - 780x + 67600
J'espère être plus claire
Merci
je ne vois toujours pas à quoi correspond x on laisse une allée de largeur x pour tourner autour ? on aurait alors ?
donc vous pouvez calculer pour L vous avez laissé un
de chaque côté donc
vous pouvez donc calculer l'aire maintenant
et pourquoi donc ne pas donner une photo du schéma d'origine qui est dans l'énoncé imprimé, vu que c'est exactement pareil techniquement que prendre une photo d'un schéma merdique ???

dans le but de perdre du temps en forçant ceux qui veulent te répondre à jouer aux devinettes ???
et puis un énoncé ce n'est absolument pas que les seules questions, cela inclut tout le texte entier qui est avant les questions !!!
(même remarque)
ce signe de totale absence de sens commun explique en grande partie pourquoi il y a des difficultés en maths !
bon, sur ce, puisque hekla semble avoir deviné le véritable énoncé, je vous laisse...
![]() Sujet ancien- ne plus donner ce lien-merci
Sujet ancien- ne plus donner ce lien-merci
Le multi-post n'est pas toléré sur l'

Bonjour
Il n'y a jamais de corrigés sur ce forum. Vous dites ce que vous avez effectué et ce qui vous empêche de continuer.
Où en êtes-vous de la résolution de ce problème ?
J'aimerais trouver la solution détaillée à ce problème :
2x²-780x+44600=0
(En sachant que je devrais trouver 69,6 à la fin) Merci.
Comment résolvez-vous une équation du second degré ?
Ce n'est pas ce qui nous intéresse. On veut trouver la valeur de pour laquelle une aire est maximale ou minimale
Le terme constant n'est pas le même que dans le sujet précédent.
Comment étudiez-vous le sens de variation d'une fonction du second degré ? sommet ou dérivée ?
Quelle est la définition de
ou
À la limite cela n'a pas d'importance puisque la dérivée est la même. Les sommets auront la même abscisse il n'y aura qu'une différence d'ordonnée et évidemment une différence sur la valeur de l'aire
Que trouvez-vous alors pour la dérivée ?


 ) :
) :

 Autres ressources en terminale
Autres ressources en terminale