Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques ExpressoPour discuter de tout et de rien... [tout]Lister tous les topics de mathématiques
Forum Expresso
Partager :

Fonction réciproque partielle

Posté par
alainpaul 29-12-14 à 15:26

Bonjour,


Pour les fonctions à plusieurs arguments ne faudrait-il pas parler de fonctions réciproques partielles?

Ainsi si l'on considère la fonction g(x,y)=xy^2-x+y^2  nous pourrions définir g^{-1}_x ,g^{-1}_y

Et nous obtenons sur les domaines de définition ad hoc
g(g^{-1}_x(x,y),y)=x,g(x,g^{-1}_y(x,y))=y

Ces écritures sont en accord avec celle des dérivées partielles:parmi les arguments un seul est variable,
et claires pour les itérées de fonctions à plusieurs arguments:g^{[n]}}_x(x,y)


Agréez-vous?


Alain

Posté par Profil amethystere : Fonction réciproque partielle 29-12-14 à 19:51

bonjour Alain Paul

pardon je ne suis pas du metier mais si tu a un peu de temps disponible peut tu m'expliquer en detail avec des exemples

car en fait j'ai du mal à suivre

Citation :
la fonction g(x,y)=xy^2-x+y^2  nous pourrions définir g^{-1}_x ,g^{-1}_y

Et nous obtenons sur les domaines de définition ad hoc
g(g^{-1}_x(x,y),y)=x,g(x,g^{-1}_y(x,y))=y


merci et au fait bonne nouvelle année camarade

Posté par Profil amethystere : Fonction réciproque partielle 29-12-14 à 23:35

re-salut ...bon ceci dit c'est à moi de chercher alors ...

soit un corps \mathbb {K} et on considère une application \mathbb {K}\times \mathbb {K}->\mathbb {K}:g(x,y)   

en fait ici cette fonction g est une loi de composition interne dans \mathbb {K}  que l'on peut tout aussi bien noter

\forall (x,y)\in \mathbb {K}^2 on vérifie z=x*y \in \mathbb {K}^2

et en admettant que (évidemment c'est pas toujours le cas comme dans ton exemple là ) cette loi * soit un groupe avec la notation 1 pour élément neutre  

je pense que là on trouverai plus avantageux d'écrire x*y=z  

donc x=z*y^{-1} et y=x^{-1}*z

mais ceci dit j'essaye de chercher tout seul en attendant j'ai pas trop compris

Posté par
alainpaulre : Fonction réciproque partielle 30-12-14 à 09:54

Bonjour,

Nous pouvons calculer g^{-1}_x   , à partir de
g(g^{-1}_x(x,y),y)=x=g^{-1}_x(g(x,y),y)

Voilà ce à quoi je pensais,


Alain

Posté par Profil amethystere : Fonction réciproque partielle 30-12-14 à 13:42

Bonjour Alain Paul  

en fait serait-il possible d'avoir un descriptif détaillé ?

car ce que j'ai dit précédemment n'est pas valable pour l'exemple que tu a donné ici

et ici c'est g(x,y)=xy^2-x+y^2

justement j'ai pas très bien compris:

Citation :
Nous pouvons calculer g^{-1}_x   , à partir de
g(g^{-1}_x(x,y),y)=x=g^{-1}_x(g(x,y),y)


Posté par
alainpaulre : Fonction réciproque partielle 31-12-14 à 10:23

Bonjour,


Le calcul nous donne:
g^{-1}_x(x,y)(y^2-1)+y^2=x   ,   g^{-1}_x(x,y)=\frac{x-y^2}{y^2-1}

g^{-1}_y(x,y)=+/-\sqrt{ \frac{x+y}{x+1}}

Il faudrait préciser les domaines de définition pour rester dans R.



Je ne possède pas de logiciel graphique;la représentation simultanée de ces quatre fonctions
nous éclairerait sur la signification géométrique de tout cela,


Alain

Posté par
weierstrassre : Fonction réciproque partielle 31-12-14 à 10:41

Bonjour,
Je ne connais pas grand chose aux fonctions de plusieurs variables, alors je peux dire des bêtises...
En effet, il me semble que la réciproque d'une fonction à deux variables peut se faire en fonction d'une variable, à la condition que la fonction soit bijective par rapport à cette variable.
Néanmoins, la réciproque de R dans R2 doit être possible car il existe des bijections de R dans R2 (néanmoins, ces fonctions sont généralement assez tordues...)

Posté par
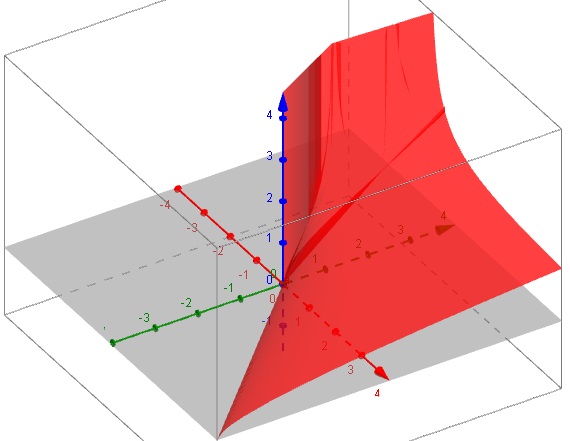
weierstrassre : Fonction réciproque partielle 31-12-14 à 11:07

voici quelques images réalisées avec geogebra.
J'ai pris l'angle ou l'on voyait le mieux la perspective, donc attention aux direction des axes.
Si vous voulez les voir sous une autre perspective, dites le moi, il n'y a pas de problèmes...
g(x,y):
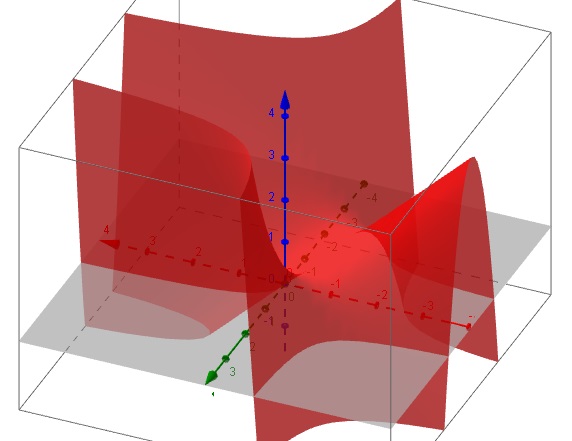
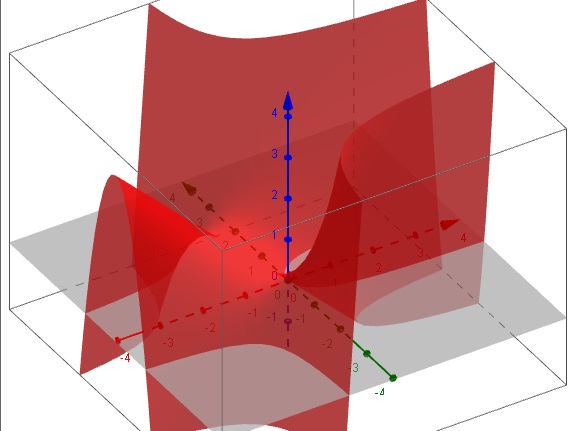
Fonction réciproque partielleFonction réciproque partielle
g-1x
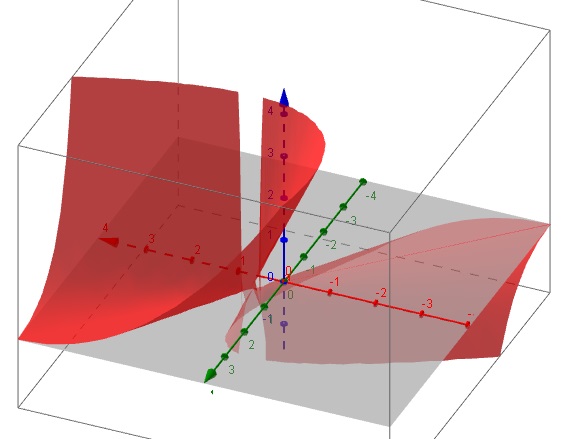
Fonction réciproque partielle

Posté par
weierstrassre : Fonction réciproque partielle 31-12-14 à 11:09

g-1y
Fonction réciproque partielle

Personnellement j'ai du mal à voir une signification géométrique....

Posté par
alainpaulre : Fonction réciproque partielle 31-12-14 à 12:25

MERCI,


Un chouette boulot!


Mon idée est simple :pour la fonction d'un argument  la réciproque
correspond à une symétrie par rapport à la bissectrice de xOy ,
y-aurait-il symétries dans notre cas par rapport à certains plans?



Alain

Posté par
weierstrassre : Fonction réciproque partielle 31-12-14 à 13:17

Oui,je connais cette propriété de symétrie, mais là, il n'y a certainement pas de symétrie sur la totalité du graphe, la forme est radicalement différente!

Posté par
alainpaulre : Fonction réciproque partielle 31-12-14 à 17:41

Bonsoir,


Si l'on ne retient que la réciproque positive  g^{-1}_y
et par exemple les valeurs x=1,y=2

Les points correspondants sont:
g(1,2)  ,  x=1,y=2,z=7
g^{-1}_x(7,2),x=7,y=2,z=1
g^{-1}_y(1,7),x=1,y=7,z=2



Alain

Posté par
alainpaulre : Fonction réciproque partielle 03-01-15 à 12:05

Bonjour,


Devrais-je abandonner tout espoir?


Nous devrions pouvoir calculer la n ième itérée
g^{[n]}_x(x,y),



Alain


Rechercher
Menu
Espace membre
21 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !