la FAQ du forum
Annuler
connectez vous
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
fonctions
Posté par 
paul34
paul34Bonjour, je suis actuellement bloqué à une question de mon dm et comme mon prof ne nous a jamais expliqué comment faire cela, votre aide serait la bienvenue:
Partie A
Soit f la fonction définie sur ℝ \ {4} par -x-(25/(x-4))
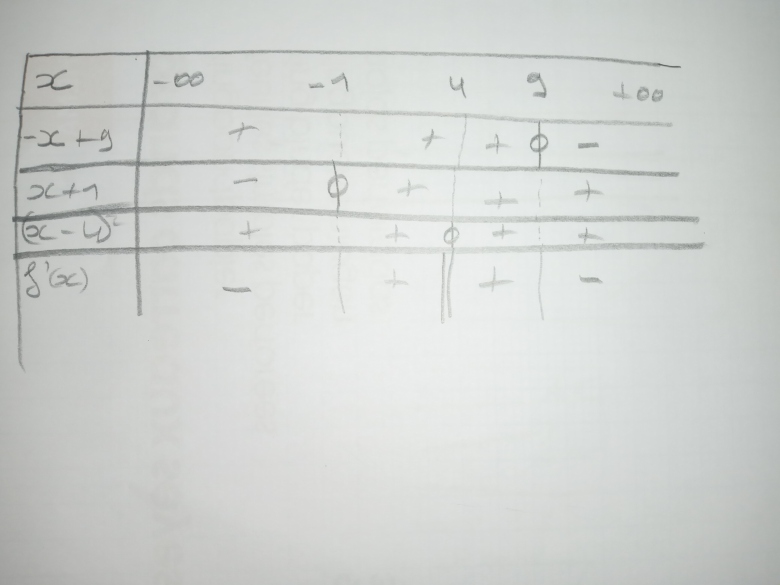
1) Montrer que pour tout x ∈ ℝ \ {4}, f'(x)= ((-x+9)(x+1))/(x-4)²
2) Dresser le tableau de signes de f ' (x) sur ℝ \ {4}, puis le tableau de variations de f sur ℝ \ {4}.
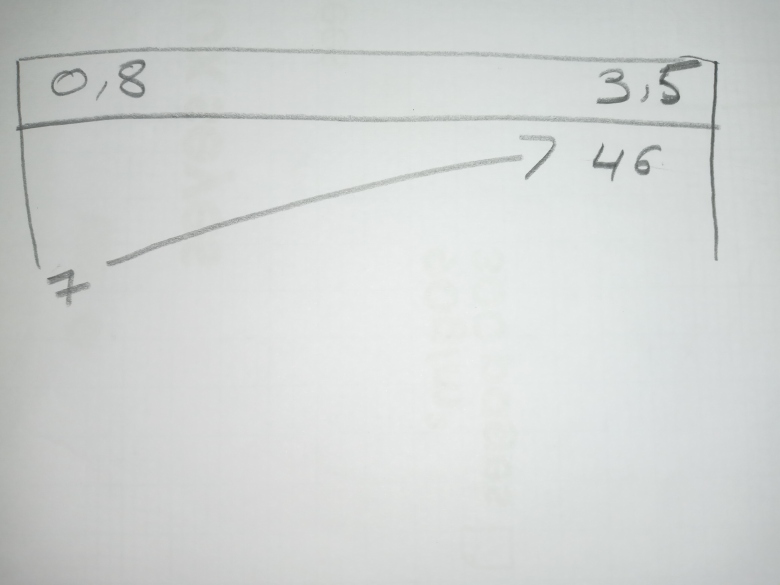
3) En déduire le tableau de variations de f sur l'intervalle [ 0,8 ; 3,5 ].
4) Déterminer le nombre de solutions de l'équation f (x) = 12 sur l'intervalle [ 0,8 ; 3,5 ].
5) Donner un encadrement au millième près de cette solution.
Partie B (Il n'y a aucun calcul à faire dans cette partie, il faut s'appuyer sur les questions précédentes)
Dans une fabrique de stylos, le coût de fabrication de x milliers de stylos est modélisé, en centaines d'euros,
par .
6) L'entreprise a payé 701,25 € ; combien a-t-elle fabriqué de stylos ?
7) Combien coûte la fabrication de 3 500 stylos ?
8) L'entreprise a payé 1 200 € ; combien a-t-elle fabriqué de stylos ?
Pour les questions 1,2,3 j'ai réussi sans problème mais j'avoue que pour la 4 je ne suis pas très sur étant donné que nous n'avons jamais traité cela en cour, j'ai trouvé une seule solution à l'équation sur l'intervalle, cela me semble assez évident ?
Pour la 5 je n'ai aucune idée de comment procéder possédant une TI
Pour la Partie B il est indiqué qu'il ne faut pas calculer mais je ne vois pas comment on peut s'aider des questions précédentes ?
toute aide est la bienvenue
merci
Bonsoir
Pour la question 4, servez-vous du tableau de variations, regardez combien de fois la flèche va passer par 12 ou utilisez le TVI
bonjour hekla,
je n'ai pas été assez rapide !
Je pense qu'il faudrait voir si le tableau de variations de paul34 est correct.
Je te laisse poursuivre, si tu es disponible. Je garde un oeil si tu dois partir. Bonne soirée.
Bonjour Leile
Je pense que le tableau de variations serait plus utile
Pourtant, ils peuvent maintenant joindre les tableaux
Je vais rester jusqu'à 19 h. Merci de prendre le relai
Donc il n'y a qu'une valeur, solution de l'équation
fonction continue strictement croissante sur
donc il existe une unique valeur
telle que
paul34, tu peux préciser la fonction f(x), stp ? dans ton énoncé, ça n'est pas lisible.
NB : dans ton tableau de signes, tu peux ne pas mettre la ligne (x-4)² car un carré est toujours positif ou nul. IL faut juste bien penser à mettre double barre sous 4 (valeur interdite).
merci pour l'explication 
Pour la 5 c'est la question où je ne comprends pas trop
Faut -il le faire avec la calculatrice ?
oui, tu peux le faire à la calculatrice.. mais montre moi f(x), il y a peut-être une autre façon de faire.
Début de la partie B : il manque aussi la fonction du cout..
Leile @ 17-02-2022 à 19:14
paul34, tu peux préciser la fonction f(x), stp ? dans ton énoncé, ça n'est pas lisible.
NB : dans ton tableau de signes, tu peux ne pas mettre la ligne (x-4)² car un carré est toujours positif ou nul. IL faut juste bien penser à mettre double barre sous 4 (valeur interdite).
paul34, tu peux préciser la fonction f(x), stp ? dans ton énoncé, ça n'est pas lisible.
NB : dans ton tableau de signes, tu peux ne pas mettre la ligne (x-4)² car un carré est toujours positif ou nul. IL faut juste bien penser à mettre double barre sous 4 (valeur interdite).
merci je vais faire cela
j'ai calculé comme vous me l'avez dit mais je ne vois pas trop où cela doit me mener
pourquoi calculer f(2) et f(2,5) ? je ne comprends pas trop
on te demande d'encadrer x pour f(x)=12.
si tu calcules f(2), tu trouves environ 10,5 donc 2, c'est pas assez.
si tu calcules f(2,5), tu trouves environ 14 : donc 2, c'est trop.
ainsi, tu peux te rapprocher de la valeur de x telle que f(x) = 12.
tu pourras vérifier que f(x)=12, pour 2,244 < x < 2,245
passons à la partie B:
la fonction est la même qu'en partie A : on peut donc utiliser ce qu'on a fait en partie A.
mais attention : le cout s'exprime en centaines d'euros, et le nombre de stylos en millier.
ce qui veut dire que x=2 correspond à 2000 stylos.
et f(x)=9 correspond à 900 euros.
tu es d'accord ?
question 1 : cout = 701,25 euros
correspond à f(x)= ??
oui, c'est f(x)=7 ! C'est une chance..
regarde ton tableau de variations : tu dois pouvoir répondre à la question : combien de stylos pour ce cout ?
oui, x=0,8 comme c'est exprimé en millier de stylos, ca donne 800 stylos.
Tu vois ?
question suivante :
3500 stylos ==> x = ??
sur ton tableau, quel f(x) as tu pour cette valeur de x ?
donc, ça donne quel cout ?
euh...
les stylos sont en abscisse, les couts sont en ordonnées
3500 stylos ==> x=3,5
f(3,5) = 46 d'après ton tableau de variations
donc cout = 4600 euros pour 3500 stylos.
allez, termine la dernière question.
cout = 1200 euros....
à toi !
Merci beaucoup pour vos explications! sans cela je pense que je serais encore en train de poirauter...
Merci à vous et passez une bonne soirée !
tu as tout compris ?
Tu as d'autres questions ?
si non, bonne soirée à toi aussi, à une prochaine fois.