Inscription / Connexion Nouveau Sujet
Geogebra encadrement d'intégrale
bonjour !
Je cherche à encadrer par géogébra une intégrale par la méthode des rectangles, c'est à dire avec des rectangles sous la courbe et des rectangles au dessus de la courbe,
je l'ai déjà vu en cour avec X² entre 0 et 1 et on observe une valeur qui tend vers 1/3
seulement là c'est avec 1/(1+t²) et je n'ai pas vraiment d'encadrement, j'ai entre 0 et n du coup, je dois encadrer cette intégrale et me rapprocher de  /2 à 10^-2 près
/2 à 10^-2 près
quelqu'un a t'il une idée de ce que je dois faire s'il vous plait ?
pardonnez moi si je ne suis pas dans la bonne section, je ne sais pas trop où mettre ça !
donc l'encadrement consiste à choisir deux sommes de termes qui convergent vers cette valeurs, ces termes étant représentatifs de la surface de rectangles qui couvrent ou sont couverts par le graphe de
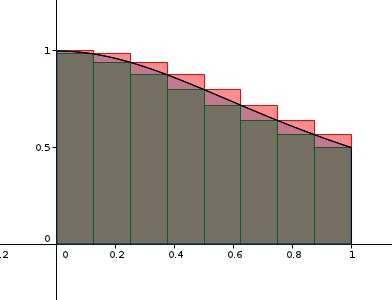
ensuite, diminuer la largeur de ces rectangles permet de diminuer l'erreur entre la surface limitée par le graphe et celle des rectangles.
Il te suffit d'exprimer comment calculer les hauteurs des rectangles verts (pour une valeur approchée par défaut) et rouges (pour une valeur approchée par excès)
D'accord, ça c'est ce que l'on avait fait pour x^2, merci de me le reexpliquer car je ne savais plus le faire, si j'ai bien compris, je dois tester avec plusieurs entiers n pour trouver lequel me donne le meilleur encadrement (à 10^-2 près)
Pour le pas que je vais utiliser (largeur des rectangle) je met une valeur faible pour avoir la meilleure approximation possible ?
Pour le calcul de l'air je fais somme des b*h de chaque rectangle vert d'un côté rouge de l'autre ?
Il faut me reprendre si je fais une erreur !
Car là tu me montres de 0 à 1 et le sujet demande de 0 à n et donc de trouver  /2 à 10^-2 près
/2 à 10^-2 près
il me semble que ton sujet fait la somme de 0 à 1 et n désigne le nombre de divisions de cet intervalle.
si tu t'imposes enfin de recopier précisément celui-ci, nous pourrons avancer sur des bases plus solides.
Salut,
j'ai demandé à mon prof aujourd'hui, il y avais une erreur dans l'énoncé, donc ce n'était pas de 0 à n comme je le prétendais mais uniquement de 0 à 1 découpé en n fois ! comme tu l'as dit dans ton premier post !
du coup la base des rectangles est de 1/n et la hauteur f(1/n) pour les rectangles verts et f(1/(n-1)) pour les rectangles rouges !
il me faut donc trouver une formule explicite de chaque suite !
pas tout à fait
il faut dans un premier temps considérer n comme une valeur constante, fixée le temps d'une évaluation.
le segment [0;1] est divisé en n segments, chacun ayant une largeur de 1/n
et les rectangles rouges (ceux qui englobent l'aire délimitée par le graphe) ont des hauteurs qui varient de f(0) à f((n-1)/n)
et les rectangles verts (ceux qui sont contenus dans l'aire délimitée par le graphe) ont des hauteurs qui varient de f(1/n) à f(1)
aire rouge :
aire verte
et l'aire délimitée par le graphe
et l'erreur faite est majorée par la différence
cette majoration te permettra de répondre à la question :
quelle valeur minimale de n faut-il choisir pour encadrer l'aire à près
(c'est maintenant qu'on augmente n pour diminuer l'erreur faite)
la réponse est n>50
tout ceci n'est possible que parce que la fonction f est décroissante sur l'intervalle.
D'accord c'est un peut la même chose que ce que l'on avais vu sur la fonction x² mais je n'avais déjà pas très bien compris du coup je n'ai pas su le refaire !
Merci à toi !
par contre, ça c'est ce que je vais écrire en justification sur ma feuille en adaptant à la rédaction ultra perfectionniste de mon prof,
mais pour ce qui est de géogebra en lui même, est-ce que je peut utiliser cette notation avec  ou est ce qu'il me faut une expression des deux suites ?
ou est ce qu'il me faut une expression des deux suites ?
tu peux utiliser les instructions Sequence[] et Somme[] pour arriver au résultat, mais c'est déjà d'une utilisation avancée.
j'ai utilisé Somme[1/(1-x²),0,1,n,1/n]
et Somme[1/(1-x²),0,1,n,1/(n-1)]
Et en augmentant n je n'ai trouvé deux décimales exactes que pour n>53 du coup je ne sais pas si c'est moi qui ai fait une erreur ou si c'est ta valeur ? Je pense plutôt que c'est la mienne mais je ne vois pas l'erreur !
après j'ai essayé SommeSupérieure[1/(1-x²),0,1,n]
et SommeInférieure[1/(1-x²),0,1,n]
et en faisant grandir n, idem j'ai trouvé un autre résultat : n>55
je n'ai certainement pas compris quelque chose !
j'ai fait une erreur dans le recopiage par contre ! c'est (n-1)/n dans la seconde somme, mais c'est comme ce que tu avais dit dans le post au dessus !
Holà, cheval,
je cite ton premier message
seulement là c'est avec 1/(1+t²)
je cite ton dernier message
j'ai utilisé Somme[1/(1-x²),0,1,n,1/n]
ta fonction est
simple erreur de recopie ? Surtout que tu insistes lourdement, par 3 fois, sur cette formule. et que cette fonction diverge (et son aire aussi) quand x tend vers 1.
aire rouge :
aire verte
et l'aire délimitée par le graphe
et l'erreur faite est majorée par la différence
or cette erreur est la différence de deux sommes de même terme général, donc ne restent plus dans la différence que les termes qui ne correspondent pas aux mêmes indices de la somme :
et si on veut obtenir la condition
et mes calculs indiquent bien pour n=50
et les fonctions que tu as utilisées SommeInf[] et SommeSup[], sont plus précises que mon propre calcul
j'utilise la formule
et la fonction intégrée SommeInf[] ou SommeSup[] utilise
parce que, vois-tu, quand on fait un calcul théorique, on obtient la condition
mais à condition que dans les sommes
aire rouge :
aire verte
on garde un nombre suffisamment grand de décimales.
si chaque terme est substitué par une valeur trop imprécise, par exemple si on ne garde, pour illustrer mon propos, que 3 décimales, alors la somme cumule ces imprécisions et le résultat final peut être très éloigné de la valeur théorique.
Donc une vraie approche en mathématiques appliquées doit aussi évaluer l'erreur faite quand on arrondit les termes de la somme, ce que doit nécessairement faire toute calculatrice. Elle ne peut garder un nombre infini de décimales...
la somme des termes approche
si on veut une valeur approchée de
la réponse à la question de l'énoncé est donc
il faut calculer au moins 100 termes (n=100) pour avoir un encadrement à
bonsoir!
Merci de ta réponse très complète !
pour le 1/(1-x²) c'est bien une erreur que j'ai fait en recopiant sur le forum, sur geogebra j'ai tapé 1+x² !
En fait l'erreur que je faisait plus haut n'étais pas vraiment une erreur !
Je croyais qu'il fallait que j'ai deux décimales exactes dans mon encadrement donc 0,78...<A<0,78...
et ça ça n'arrive que à n>55 ! d'où mon erreur ! Alors qu'en fait il fallait soustraire les deux intervalles et donc là du coup je trouve la même chose que toi !
pour ce qui est de l'augmentation des erreurs en fonction des décimales oui mon prof me l'avais déjà expliqué lorsque l'on faisait des calculs sur excel, c'est vrai que le résultat peut devenir aberrant dépassé un certain rang !
en tout cas merci beaucoup ! C'est la touche finale de mon DM, hors barème mais ça prouve que j'ai voulu me bouger un peu pour comprendre quel était le but du DM !
Bonne soirée !


