Bonsoir
Pouvez vous m'aider à résoudre cet exercice.
Merci d'avance. En effet j'ai été abscent au cours et je ne c'est pas comme résoudre ces questions.

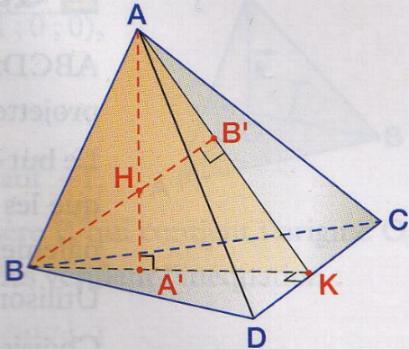
ABCD est un tétraèdre, A est le projeté orthogonal de A sur le plan (BCD) et B et celui de B sur le plan (ACD)

1. On suppose que ABCD est un tétraèdre orthocentrique.

a) Démontrez que les droites (CD) et (BA') sont perpendiculaires. On note K le point d'intersection de (CD) et de (BA').
b) Démontrez que les droites (BC) et (DA') sont perpendiculaires ; déduisez-en que A' est l'orthocentre du triangle BCD.
c) Démontrez rapidement, en procédant comme aux questions a) et b), que le point B' est l'orthocentre du triangle ACD.
d) Démontrez que K appartient à la droite (AB').
Déduisez-en que les droites (AA') et (BB') sont sécantes.
e) Démontrez que les quatre hauteurs du tétraèdre sont concourantes.
Le point de concours des hauteurs est appelé orthocentre du tétraèdre orthocentrique.

2. Étude d'une réciproque

Démontrez le résultat suivant : Dans un tétraèdre ABCD, si le projeté orthogonal A' de A sur le plan (BCD) est l'orthocentre du triangle BCD, alors le tétraèdre ABCD est orthocentrique.