Inscription / Connexion Nouveau Sujet
géométrie dans un triangle
bjr! j'ai besoin de votre aide.
M est un point intérieur au triangle ABC. A' est le point de rencontre des droites (AM) et (BC).
Montrer que où
et
représentent les aires des triangles MAB et MAC.
Merci d'avance.
Tu pourrais raisonner sur des aires de triangles de la figure, savoir les triangles A'AB et A'AC, puis les triangles A'MB et A'MC .
Bonjour
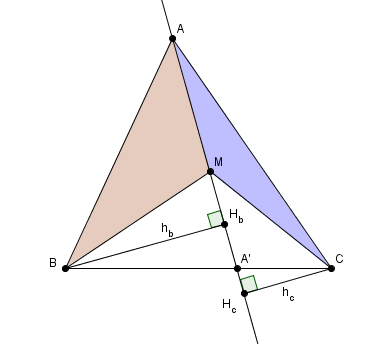
les deux triangles ayant la même base AM, le rapport des aires sera le rapport des hauteurs : ensuite c'est juste le théorème de Thalès dans les triangles et
où
et
sont les pieds des hauteurs issues de B dans AMB et de C dans AMC
joli, mais qui sait encore que si a/b = c/d, alors a/b = c/d = (a-c)/(b-d) ?
Sinon, ce que je proposais ne nécessitait aucun autre triangle que ceux de l'énoncé, du coup je ne comprends pas trop le message de 14h18 ?
Bonjour,
le message de 14h18 fait suite au message de 10h53
et qui est la suite de la méthode (certes inutilement compliquée) qui avait été imaginée par le demandeur.
illustration de la méthode directe :
(j'avoue, j'ai eu la flemme d'en faire une autre que papier/crayon 
)
Annuler
connectez vous