Inscription / Connexion Nouveau Sujet
géométrie du triangle
Bonjour
j'ai besoin de votre aide pour résoudre ce problème dont voici l'énoncé :
Soit le triangle ABC inscrit dans le cercle (Co) de centre O et de rayon R, I le centre du cercle (Ci) de rayon r, incrit dans le triangle ABC, et d la distance OI.
La droite (AI) recoupe (Co) en 
, et la droite (O)recoupe (BC) en H.
Soit d'autre part k la projection de I sur (O)
1/ Montrer que le cercle BIC a pour centre et que
=
2/ Démontrer la relation
3/ En déduire la relation d'Euler : d² = R²- 2Rr.
Je suis pour l'instant bloqué à la question 1.
B,C et sont cocycliques, donc OB = OC (et O appartient à la médiatrice de [BC]) = O.
I 
(O) qui est bissestrice intérieure de l'angle BAC
Y aurait-il une propriété caractéristique des bissectrices intérieures d'un triangle avec ses médiatrices ou le cercle qui lui est circonscrit (ici Co) ?
Ci-dessous un schéma :
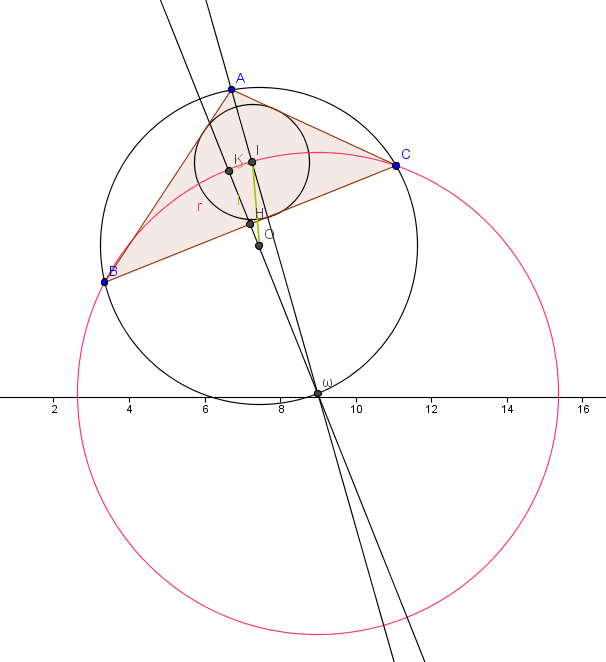
Merci de m'aider à avancer.
Bonjour,
I
(O) qui est bissestrice intérieure de l'angle BACla bissectrice de l'angle A n'est pas la droite (O
) (elle ne passe même pas par A) et de toute façon I n'est pas sur la droite (O) non plus...
tu voulais dire la droite (A
)
mais ceci c'est juste répéter la définition du point
de l'énoncé ...
Y aurait-il une propriété caractéristique des bissectrices intérieures d'un triangle avec ses médiatrices ou le cercle qui lui est circonscrit (ici Co)
, et c'est justement ce qu'il faut montrer ici
bien entendu si on "connait" cette propriété, l'exo tombe de suite (= est sans intérêt, puisque l'exo c'est justement cette propriété)
commencer par prouver que
est sur la médiatrice de [BC] en considérant les angles inscrits qui interceptent les arcs B et C
bien entendu pour la suite il va falloir faire intervenir que I est non seulement sur la bissectrice intérieure de l'angle A mais aussi sur la bissectrice intérieure de l'angle B (I n'est pas n'importe quel point de la bissectrice)
puis le plus simple à mon avis est de faire intervenir le point J, centre du cercle exinscrit dans l'angle A.
(le cercle BIC aura pour diamètre IJ)
>>Mathafou
bonjour
juste quelques mots pour l instant pour te dire merci pour ces premiers éléments de réponse qui m'aident à avancer ; je continue mes réflexions avec un différé par rapport à ce que j'avais prévu. Je reviendrai prochainement sur ce sujet, ne pense pas que je m'en désintéresse
Bonsoir
je suis parvenu à établir que B I et C sont cocycliques sur un cercle de centre , grâce à tes suggestions et à des théorèmes du cours.
Par contre je n'arrive pas encore à démontrer que ; j'ai pensé à la puisance du point par rapport au cercle inscrit dans le triangle ABC, mais je n'aboutis pas puisque les droites de l'énoncé passant par
coupent ce cercle en des points non connus.
Une suggestion svp ? Merci par avance
quand même
Je viens juste de voir ton "up"
en fait je n'avais pas d'idée faramineuse sur le sujet et je n'avais pas creusé d'avantage.
la liaison avec le cercle inscrit n'est pas claire du tout.
pour l'instant ce cercle inscrit n'existe même pas (on n'a en réalité que défini I comme intersection des bissectrices et rien d'autre)
alors le faire intervenir ... je me demande bien comment !
en tout cas la formule demandée ressemble trop à un produit scalaire ou une puissance par rapport à un cercle pour que ce soit une coïncidence !
reste à trouver lequel !
soit 
le point diamétralement opposé à sur le cercle Co
calculons le produit scalaire de deux manières
1) en le projetant sur (C)
2) en le projetant sur () (c'est à dire la droite (O)
Excellente idée ; merci bcp pour ce conseil très judicieux
je passe à la suite et si besoin reviendrai
J'ai résolu la question 2 en posant P milieu de [O].
Pour la question 3, à partir des résultats des questions 1 et 2 et en développant, j'arrive à
, mais je ne fais pas le lien entre KH et r, rayon du cercle inscrit dans le triangle ABC.
Une idée ?
Merci par avance
IK, perpendiculaire à HK par construction
et HK perpendiculaire à BC
donc IK parallèle à BC
en d'autres termes, HK est égal à la distance de I à BC...
Annuler
connectez vous