Inscription / Connexion Nouveau Sujet
Géométrie vectorielle
Bonjour tout le monde, je m'excuse de vous déranger mais j'ai besoin d'un petit coup de pouce pour les questions 4 et 5 de cet exercice.
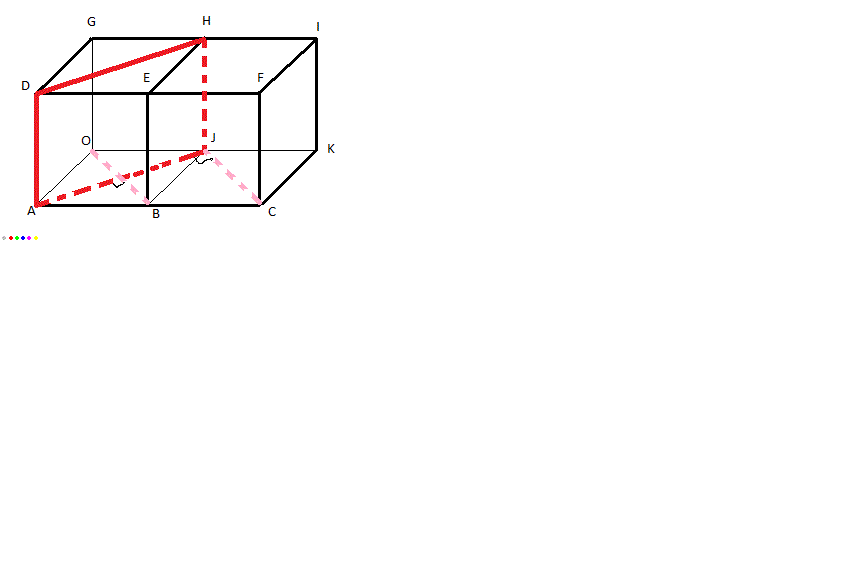
Deux cubes d'arête 1 sont disposés comme l'indique la figure ci dessous.L'espace est rapporté au repère orthonormé (O,OA,OJ,OG)
Pour chaque question,une seule réponse est exacte.Identifiez la.
Justifiez vos réponses.
1.Le triangle GIB est:
a.rectangle b.équilatéral c.isocèle
2.Le point M tel que 2MO-MA+MC=0 est le point:
a.K b.I c.J
3.Une représentation paramétrique de la droite (KE) est:
a.x=t
y=2+t, t appartient à R
z=t
b.x=3+4t
y=t t appartient à R
z=4t
c.x=1-t
y=1+t t appartient à R
z=1-t
4.Le volume du tétraèdre DACH est:
a.1/2 b.1/6 c.1/3
5.La distance de C au plan (ADH) est:
a.2 b.1/2 c/
2
Mes réponses sont 1c ; 2c ; 3c et pour les deux autres, je bloque.
V DACH= (base X hauteur) / 3
La base est ADC et AADC=(AD X AC)/2 = (1 X 2)/2 = 2/2 = 1
Mais après, si cela est juste, je n'arrive pas à déterminer la hauteur et à la calculer.
Merci beaucoup pour votre aide et je vous souhaite de passer de bonnes fêtes de fin d'année.
Bonjour, bonnes Fêtes à toi aussi.
la hauteur d'une pyramide relative à une certaine base est la perpendiculaire à cette base issue du sommet opposé
donc ici la perpendiculaire au plan (ADC) issue de H
(rappel, un plan est infini
de même que la hauteur d'un triangle peut "tomber" en dehors de la base, la hauteur d'une pyramide peut "tomber" en dehors de la base)
pour la dernière question tu dois identifier la perpendiculaire à (ADH) issue de C
que penses tu de la nature du triangle AJC ? conclusion ...
(rappel : pour qu'une droite soit perpendiculaire à un plan etc..)
Bonjour, je vous prie de bien vouloir m'excuser pour mon moment d'absence.
Merci de m'avoir répondu.
La perpendiculaire au plan (ADC) issue de H est [HE] = 1
Donc on aurait:
V DACH= (base X hauteur) / 3
= (1 X 1) / 3
= 1 / 3
Donc la bonne réponse pour la question 4 est encore la c ?
5. La perpendiculaire à (ADH) issue de C est [CO].
AJC est isocèle car AJ = JC = 2 mais je ne vois pas trop où aller avec cela ...
Si, vous avez raison mais je n'étais pas sûre donc j'ai préféré ne rien écrire.
Comment peut-on déterminer la distance de C au plan (ADH) avec cela ?
Tu pourrais déterminer la droite intersection des plans (ADH) et (ACKO), puis faire une figure à plat du rectangle ACKO avec cette droite le segment BJ.
Bonjour,
[BO] // [CJ].
La perpendiculaire à (ADH) issue de C est [CJ].
Or, si l'on se place dans le triangle AJC rectangle en J (avec [AJ] = [JC]) , d'après le théorème de Pythagore, nous avons:
AC² = AJ² + JC²
<=> 2² = AJ² + JC²
<=> 4 = 2 JC²
<=> 2 = JC²
Donc JC =2
La distance de C au plan (ADH) est donc 2 si je ne me suis pas trompée.
Est-ce normal que pour toutes les questions, je trouve que la bonne réponse est toujours la C ?
Bonsoir,
Merci de m'avoir répondu.
Cela m'inquiète parce que pour toutes les questions j'ai trouvé que la bonne réponse était la c donc je me demande si je ne me suis pas trompée...
Est-ce normal que j'ai ces résultats: 1c; 2c; 3c; 4c et 5c ?
Pourquoi pas ? La réponse c) est bien toujours la bonne.
C'est peut-être simplement pour inquiéter les élèves peu sûrs de leurs résultats . . .
Annuler
connectez vous