Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques AutreForum traitant des mathématiques, un peu moins scolaires AlgorithmiqueForum consacré aux algorithme [tout]Lister tous les topics de mathématiques
Niveau algorithmique
Partager :

Intersection de deux sphères

Posté par
mielle 15-10-13 à 21:45

Bonjour,
En faite je ne suis pas mathématicienne , alors peut être mes questions sont triviales pour vous .

J'ai deux cercles (ou spheres) ou je connus le centre des deux sphères
centre1(x1,y1,z1)
centre2(x2,y2,z2)
et le radius des deux sphères aussi donnée par ruduis1, raduis2
je veux connaitre les coordonnées des points d'intersections des deux sphères (dans l'image sont en rouge)

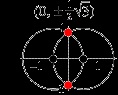
Intersection de deux sphères

comment puis je faire ça

  

Posté par
mathafou Moderateurre : Intersection de deux sphères 16-10-13 à 11:00

Bonjour,
l'intersection de deux sphères (puisque tu parles de 3 coordonnées c'est donc dans l'espace et pas juste sur le plan de ta figure) l'intersection de deux sphères, donc, est un cercle et pas juste deux points dont on pourait calculer les coordonnées. Ta question telle que tu la poses n'a donc aucun sens.

calculer les coordonnées "dans le cas général" est assez filandreux (des bardées de X1 X2 etc et je ne le ferais pas ici

l'équation du cercle d'intersection des deux sphères se fait en écrivant l'équation des deux sphères et en les retranchant membre à membre.
on obtient ainsi l'équation d'un plan qui contient le cercle (s'il y a intersection !)
l'équation du cercle est alors le système
{ équation d'une des sphères
{ équation du plan

et l'on peut obtenir une équation paramètrique de ce cercle en trouvant son centre (intersection de la ligne des centres et du plan) et son rayon R (Pythagore) et en écrivant \vec{\Omega M} = \vec{u}cos(t) + \vec{v}sin(t) où et sont deux vecteurs orthogonaux du plan (P) et de norme R.

bref c'est "un peu compliqué" et d'après ce que je devine "pas du niveau".

c'est plus simple s'il s'agit de cercles dans un même plan
mais alors il n'y a pas de "z" là dedans, juste deux coordonnées x et y.
et deux cercles, quand ils se coupent, se coupent bien en deux points.

la méthode est la même avec z en moins, la soustraction membre à membre des deux équations de cercles donne une droite (c'est leur axe radical) et les points sont solutions du système :

(x-X1)2 + (y-Y1)2 = R12 (il appartient au premier cercle)
2(X1 - X2)x + 2(Y1 - Y2)y + X22 - X12 + Y22 - Y12 = R22 - R12 (l'axe radical)
que l'on résoud par substitution en éliminant y entre ces deux équations (extraire y de l'équation de la droite et le substituer dans l'équation du cercle) ce qui donne une équation du second degré en x et les deux points d'intersection.

cela se simplifie encore si les cercles sont particuliers (même rayon, symétriques par rapport à l'axe Oy, centrés sur l'axe Ox etc)
dans le cas simple de ta figure juste Pythagore donne directement l'ordonnée des points d'intersection :

y2 = R2 - X12
c'est à dire :
\boxed{y = \pm \sqrt{R^2 - X_1^2}}
(leur abscisse est bien entendu x = 0 : ils sont sur l'axe de symétrie Oy)

Posté par
miellere : Intersection de deux sphères 16-10-13 à 22:51

Merco pour votre explication
en faite je cherche que sur une point d'intersection.
y a t il une possibilité de trouver le changement de repère pour passer de  repère global à un repère local où les axes x et y locaux seraient dans le plan (donc avec un Zlocal=0). Et là on peux travailler comme on veut avec des formules 2D.

Posté par
mathafou Moderateurre : Intersection de deux sphères 16-10-13 à 23:36

rien compris.
tu veux dire que tu as deux cercles dans un seul plan de l'espace ?
comment est défini ce plan ?? ton "énoncé" est beaucoup trop imprécis pour qu'on en fasse quoi que ce soit.

Posté par
miellere : Intersection de deux sphères 17-10-13 à 12:10

oublié mon idée
dans mon cas je veut juste trouvé une seule point d'intersection
est ce que c'est possible ?

Posté par
mathafou Moderateurre : Intersection de deux sphères 17-10-13 à 12:25

le problème est bien de trouver l'intersection de quoi, définis comment ?
le reste est de toute façon du calcul, mais si on ne sait pas clairement ce qu'on cherche et d'où on part on ne peut en faire aucun de calcul !

Posté par
miellere : Intersection de deux sphères 17-10-13 à 12:29

je cherche à trouvé une point d'intersection de deux sphères

Posté par
mathafou Moderateurre : Intersection de deux sphères 17-10-13 à 13:16

donc un point au hasard parmi l'infinité des points qui sont sur l'intersection de deux sphères, intersection qui est un cercle comme déja dit et les calculs sont ceux suggérés.

équation des deux sphères
équation du plan radical (celui dans lequel se trouve le cercle)
centre du cercle = intersection de la ligne des centres et du plan radical
intersection de ce cercle par un plan au hasard passant par le centre du cercle, et différent du plan radical

ne t'attends pas à une formule il n'y en a pas (ou plutôt elle est trop monstrueuse pour être écrite par qui que ce soit de sensé) : les coordonnées s'obtiennent par l'éxécution pas à pas des étapes décrites ci dessus.
Reste le choix "au hasard" du plan d'intersection. et le choix "au hasard" parmi les deux points d'intersection du cercle et de ce plan là...

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 07:22

Bonjour Mielle
Bonjour Mathafou (si tu peut me permettre)
effectivement je ne savais pas que tu n'est pas mathématicienne et que tu travaille independamment à ce que je vois (je ne lit pas tous les fils) (sinon pour le fil où je t'ai répondu je dois attendre tes deux réponses pour t'apporter mon aide en espérant qu'elle soit efficace et juste)
d'ailleurs là aussi j'ai une question qui est en rapport avec le fil dont je parle

si je peut me permettre pour ce fil alors oui il est possible de définir tous les points communs aux deux sphères (si ils existent donc on peut donner la condition pour qu'ils existent) à partir du moment que tu dispose de cela : (or d'après ton premier post tu en dispose)

tu dispose donc de deux sphères S1 et S2 de rayon respectivement   R_1 pour la première sphère S1 et de rayon   R_2 pour la seconde sphère S2 de plus de centre respectivement C=(c_1,c_2,c_3) pour la première sphère S1 où les composantes c_i désignent la position du point C et de centre D=(d_1,d_2,d_3) pour la seconde sphère S2 où les composantes d_i désignent la position du point D

Méthode à partir des données que dont tu dispose

0)il est admis ici que les point C et D sont distincts alors on va au 1)

1)la première chose à faire est de definir les conditions qui font qu'il existe un ou une infinitée de points commun à ces deux sphères ensuite si la condition est remplie on va au 2)

2)on va rechercher un point K=(k_1,k_2,k_3) particulier (donc pas n'importe lequel) et situé sur le segment CD et on va au 3)

3)après soit ce point K est l'unique point commun aux deux spheres(il s'agit alors du point de contact entre ces deux sphères soit il n'est pas un point qui est commun à ces deux sphères et on va au 4)

4)on se donne un point au choix L=(l_1,l_2,l_3) tel que
le produit scalaire \vec {KC}.\vec {KL}=0
donc

((c_1-k_1).(l_1-k_1))+((c_2-k_2).(l_2-k_2))+((c_3-k_3).(l_3-k_3))=0

dans ce cas on verifie aussi \vec {KD}.\vec {KL}=0
ce qui signifie que le segment KL est orthogonal au segment CD auquel appartiens le point K et on va au 5)

5)on détermine un point M tel que par le produit vectoriel on obtiens
\vec {KC}\wedge \vec {KL}=\vec {KM}
ce faisant on a construit un plan (on va l'appeler le plan O) auquel appartiennent les points K,L,M et aussi tous les points qui sont communs aux deux spheres
de plus tous ces points forment un cercle sur le plan O et ce cercle est de centre K on passe au 6)

6) on determine l'ensemble des points communs aux deux sphères

pour t'aider à comprendre comment on va faire précisement il serait utile que tu vois un peu les vecteurs

as tu des questions sur les vecteurs?

Posté par
miellere : Intersection de deux sphères 29-10-13 à 16:26

Merci pour ton aide et pour tes réponse

Citation :
as tu des questions sur les vecteurs?

Non , je connus comment travailler avec les vecteurs et même j'utilise une bibliothèque qui me fait ce genre de calcul(produit vectoriel,produit scalaire...)

Mais pour le moment je ne vois pas un rapport entre ma question concernant les angles et ce post ?

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 16:58

Bonjour Camarade Mielle

en fait juste le rapport des vecteurs parce que je les utilise dans ce fil
comme dans l'autre

donc est-ce que ma methode en six points te parle?

en fait elle est tres simple mais comme je sais pas si tu la "visualise" peut être que...

si oui je la détaille sinon je ne vois pas d'autre méthode pour résoudre ce fil

Posté par
miellere : Intersection de deux sphères 29-10-13 à 17:18

j'ai re-lire ta réponse en utilisant les vecteurs
j'ai compris 80% de la méthode
si la solution unique de mon problème est d'utiliser les vecteurs vous pouvez m'expliquer et je  vais faire l'effort afin de comprendre la manipulation des vecteurs

Merci une autre fois  parce que vraiment j'ai besoin d'aide d'un mathématicien

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 17:32

Camarade Mielle je suis pas mathématicien!
comme vous en fait!

bon là tout de suite je dois partir
vous verrez c'est tres simple quelques posts  mais rien de méchant
car votre fil est précis dans sa demande
on reste dans le plan et l'espace au fond c'est pas la mort

je reviens

Posté par
miellere : Intersection de deux sphères 29-10-13 à 17:40

Oh , vous être pas mathématicien ?
bien mais vous avez un bon niveau en math
Moi non , je peux trouver moi même en algèbre mais la géométrie c'est hors mes compétence


Merci

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 19:05

Re-bonjour

bon là tout de suite juste un debut (mais au final en terme d'outils il n'y aura pas grand chose le plus limite c'est justement ce post là) pour avoir les outils qui vont permettrent de resoudre le fil

ce sont des outils tres simples même si ce post est un peu long et que vous savez ça (comme je sais pas trop où vous en êtes mieux vaut ne pas laisser un truc à coté
on va se projetter dans l'espace
un point P=(p_1,p_2,p_3) possedent donc trois composantes p_iqui le positionne
ces composantes on les appelles des scalaires
ok
si on prend deux points P=(p_1,p_2,p_3) et Q=(q_1,q_2,q_3)
alors si donc ces points sont un seul et même point on a
p_1=q_1 , p_2=q_2 , p_3=q_1

sinon ils sont distincts
dans ce cas on peut construire un segment de droite PQ

quand on parle du vecteur \vec {V}=\vec {PQ}=(v_1,v_2,v_3)=(q_1-p_1,q_2-p_2,q_3-p_3) donc ici
v_1=q_1-p_1 , v_2=q_2-p_2 , v_3=q_3-p_3

en le nommant \vec {PQ} on imagine une fleche partant du point P on le nomme point d'application du vecteur et arrivant au point Q

mais si je te dit \vec {V}=\vec {PQ}=(v_1,v_2,v_3) sans que tu connaisse la position des deux point P et Q
alors tu peut pas dire que par les informations dont tu dispose sur ce vecteur et qui sont les scalaires v_i que tu puisse considerer que ce vecteur possede un point point d'application

ce qui compte chez un vecteur c'est la longueur du segment des deux points qui le compose,sa direction et son sens

pour comprendre si tu prend deux droites paralleles dans l'espace elles ont mêmes direction et pourtant elles sont distinctes de plus si tu imagine un point se baladant sur l'une des droite et pareil un autre point se baladant sur l'autre droite
tu peut voir si ces points vont dans le même sens et la longueur qu'il parcourent

ce qui fait que si deux vecteurs ont mêmes direction et même sens et de plus ont même longueur(la "longueur d'un vecteur se nomme norme d'un vecteur)eh
bien en fait il s'agit du même vecteur même si ils n'ont pas le même point d'apllication

ce qui fait prenons quatre points P,Q,F,G tels que  

\vec {V}=\vec {PQ}=\vec {FG}=(v_1,v_2,v_3)=(q_1-p_1,q_2-p_2,q_3-p_3)=(g_1-f_1,g_2-f_2,g_3-f_3) alors bien que ces points puissent êtres tels que F \neq P   et G \neq  Q et bien cela n'empêche que  \vec {PQ}=\vec {FG}=(v_1,v_2,v_3) de plus les informations

v_i ne te permettent pas de connaitre les positions de ces points

parler d'un vecteur en le decrivant uniquement que par ses composantes c'est parler d'un vecteur dont le point d'application est l'origine du repere par lequel tu definit les positions de tout point
et un vecteur nul est en fait un vecteur dont la norme est nulle

pour un vecteur \vec {V}=(v_1,v_2,v_3)
sa norme est definie par ||\vec {V}||=\sqrt {v_1^2+v_2^2+v_3^2}  

est-ce que jusqu'ici ça va?

là je repart  

je reviendrai

Posté par
miellere : Intersection de deux sphères 29-10-13 à 20:06

Oui trés bien ,
j'ai tout compris

en faite t'es un professeur ou quoi? t'as une bonne méthode d'explication
Mreic une autre fois

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 20:29

Mielle non! je suis pas prof non plus
Camarade tu sais on se ressemble beaucoup (ça t'imagine pas)
il reste encore un post pour les outils(à peu près aussi long environ)  et c'est bon on attaque ton fil direct(excuse moi demain : là je peux pas Camarade)
belle soirée Camarade

Posté par
miellere : Intersection de deux sphères 29-10-13 à 20:32

On rassemble ? je pense pas

D'accords on continue demain

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 20:39


Mielle j'ai pas dit rassembler j'ai dit ressembler
bon en tout cas je suis pas prof alors vous voyez...
à demain Camarade

Posté par
miellere : Intersection de deux sphères 29-10-13 à 20:50

Oui erreur de frappe ressemble

Posté par Profil amethystere : Intersection de deux sphères 29-10-13 à 21:02

alors oui on se ressemble Camarade
c'est pour ça qu'on se comprend enfin on essaye et non pas parce que je suis prof car ça c'est tout ce qu'il y a de plus faux
belle soirée Camarade Mielle

Posté par Profil amethystere : Intersection de deux sphères 30-10-13 à 19:25

Bonsoir Mielle
excusez moi je suis en retard
je dernier post avant la résolution est un peu long je vous file pour cette nuit

@+tard Mielle

Posté par Profil amethystere : Intersection de deux sphères 30-10-13 à 22:54

Bonsoir Mielle
suite et fin en ce qui concerne les outils puis on passe à la résolution

remarque n°0: ce post étant long il a été vérifié plusieurs fois avant de poster
cependant contrairement à l'autre- dont je te recommande de relire- il est pas compliqué il suffit d'appliquer ce qui y ait dit
et enfin il m'arrive de faire des fautes mais je t'assure même s'il est tôt je l'ai vérifié plusieurs &  plusieurs  fois

donc ainsi qu'on a dit la distance entre deux point P=(p_1,p_2,p_3) et Q=(q_1,q_2,q_3) est donnée par la norme du vecteur
\vec {PQ}=(q_1-p_1,q_2-p_2,q_3-p_3)  
on obtiens donc
distance PQ=||\vec {PQ}||=\sqrt {(q_1-p_1)^2+(q_2-p_2)^2+(q_3-p_3)^2}

par ailleurs un vecteur nul peut se noter \vec {0}=(0,0,0)

par conséquent ||\vec {0}||=0

les vecteurs ici décris sont des éléments d'un R-espace vectoriel que l'on note \mathbb {R}^3 et que l'on nomme espace vectoriel euclidien

_____________________

cet ensemble est munis du produit par un scalaire
il s'agit d'une application \mathbb {R}\times  \mathbb {R}^3 ->\mathbb {R}^3  
\lambda \in \mathbb {R} est un scalaire et
\vec {X}=(x_1,x_2,x_3) \in \mathbb {R}^3   est un vecteur on obtiens

\lambda .\vec {X}=(\lambda .x_1, \lambda .x_2, \lambda .x_3)\in \mathbb {R}^3   est un vecteur

on verifie

\lambda . \vec {X}=\vec {X}.\lambda   Commutativité

(\lambda _1.\lambda_2).\vec {X}=\lambda _1.(\lambda_2 .\vec {X})

associativité par rapport au produit des scalaires

(\lambda _1+\lambda_2).\vec {X}=(\lambda _1.\vec {X})+(\lambda_2 .\vec {X})
distributivité par rapport à l'addition des scalaires

1 . \vec {X}=\vec {X}   élément neutre \lambda =1  

____________

cet ensemble est munis de l'addition vectorielle
il s'agit d'une application \mathbb {R}^3\times  \mathbb {R}^3 ->\mathbb {R}^3  

\vec {X}=(x_1,x_2,x_3) \in \mathbb {R}^3   et  \vec {Y}=(y_1,y_2,y_3) \in \mathbb {R}^3   sont des vecteurs on obtiens

\vec {X}+\vec {Y}=(x_1+y_1, x_2+y_2, x_3+y_3)\in \mathbb {R}^3   est un vecteur

on verifie

\vec {X}+\vec {Y}=\vec {Y}+\vec {X}   Commutativité

(\vec {X}+\vec {Y})+\vec {Z}=\vec {X}+(\vec {Y}+\vec {Z}) associativité

\lambda.(\vec {X}+\vec {Y}) =(\lambda.\vec {X} )+(\lambda .\vec {Y} )

le produit par un scalaire est distributif par rapport à l'addition des vecteurs

\vec {0} + \vec {X}=\vec {X}   élément neutre \vec {0}  

symétrie on note -\vec {X}=(-1).\vec {X}
on vérifie \vec {X}-\vec {X}=\vec {0}

de plus -(-\vec {X})=\vec {X}


___________

cet ensemble est munis du produit scalaire
il s'agit d'une application \mathbb {R}^3\times  \mathbb {R}^3 ->\mathbb {R}  

\vec {X}=(x_1,x_2,x_3) \in \mathbb {R}^3   et  \vec {Y}=(y_1,y_2,y_3) \in \mathbb {R}^3   sont des vecteurs on obtiens

\vec {X}.\vec {Y}=x_1.y_1+x_2.y_2+x_3.y_3 \in \mathbb {R}   est un scalaire

on verifie

\vec {X}.\vec {Y}=\vec {Y}.\vec {X}   Commutativité
\lambda.(\vec {X}.\vec {Y}) =(\lambda .\vec {X}).\vec {Y}  
le produit par un scalaire est associatif par rapport au produit scalaire

(\vec {X}+\vec {Y}).\vec {Z}=(\vec {X}.\vec {Z})+(\vec {Y}.\vec {Z}) distributivité par rapport à l'addition des vecteurs

remarque n°1
\vec {X}.\vec {X}=\vec {X}^2
est une notation acceptée

remarque n°2
la norme d'un vecteur
||\vec {X}||=\sqrt {\vec {X}^2}

remarque n°3
Soit un vecteur \vec {X}
alors si on vérifie \vec {X}^2=0
alors dans ce cas ce vecteur est nul et on verifie \vec {X}=\vec {0}  

remarque n°4
Soient deux vecteurs non nuls \vec {X}\neq \vec {0}   et  \vec {Y}\neq \vec {0}  

alors si on vérifie \vec {X}.\vec {Y}=0 on dit alors que ces deux vecteurs sont orthogonaux
___________

on l'a vu la norme d'un vecteur est une application \mathbb {R}^3   ->\mathbb {R}  

\vec {X}=(x_1,x_2,x_3) \in \mathbb {R}^3   est un vecteur on obtiens

||\vec {X}||=(x_1,x_2,x_3)=\sqrt {x_1^2+x_2^2+x_3^2} \in \mathbb {R} est un scalaire positif

par ailleurs pour tout vecteur non nul \vec {X}\neq \vec {0} alors

\frac {1}{||\vec {X}||}.\vec {X} est le vecteur unitaire de \vec {X}\neq \vec {0}

dans ce cas on vérifie ||\frac {1}{||\vec {X}||}.\vec {X}||=1

la norme d'un vecteur unitaire est 1

___________

on peut aussi munir cet ensemble du produit vectoriel

il s'agit d'une application \mathbb {R}^3\times  \mathbb {R}^3 ->\mathbb {R}^3  

\vec {X}=(x_1,x_2,x_3) \in \mathbb {R}^3   et  \vec {Y}=(y_1,y_2,y_3) \in \mathbb {R}^3   sont des vecteurs on obtiens

\vec {X}\wedge \vec {Y}=\vec {Z}=(z_1,z_2,z_3)\in \mathbb {R}^3   est un vecteur

avec

z_1=x_2.y_3-x_3.y_2

z_2=x_3.y_1-x_1.y_3

z_3=x_1.y_2-x_2.y_1


on verifie

\vec {X}\wedge \vec {Y}=-(\vec {Y}\wedge \vec {X})   Anti-Commutativité

\lambda .(\vec {X}\wedge \vec {Y})=(\lambda .\vec {X})\wedge \vec {Y}  
le produit par un scalaire est associatif par rapport au produit vectoriel

(\vec {X}+\vec {Y})\wedge \vec {Z}=(\vec {X}\wedge \vec {Z})+(\vec {Y}\wedge \vec {Z}) distributivité par rapport à l'addition des vecteurs

___________

on peut aussi munir cet ensemble d'une application \mathbb {R}^3\times  \mathbb {R}^3 ->\mathbb {R}^3  

que l'on note

\vec {X}=(x_1,x_2,x_3) \in \mathbb {R}^3   et  \vec {Y}=(y_1,y_2,y_3) \in \mathbb {R}^3   sont des vecteurs on obtiens

\vec {X}\times \vec {Y}=(\vec {X}^2.\vec {Y})-((\vec {X}.\vec {Y}).\vec {X})\in \mathbb {R}^3  

___________

enfin pour tous vecteurs non nuls \vec {X}\neq \vec {0}   et  \vec {Y}\neq \vec {0}  

on considère la notation

\vec {X}*\vec {Y}=\sqrt {\frac{\vec {X}^2.\vec {Y}^2-(\vec {X}.\vec {Y})^2}{U}}.(\vec {X}\times \vec {Y})\in \mathbb {R}^3  

avec

U=(\vec {X}^2.\vec {Y})^2.\vec {X}^2+((\vec {X}.\vec {Y}).\vec {X})^2.\vec {X}^2-2(\vec {X}.\vec {Y})^2.\vec {X}^2.\vec {X}^2

___________Propriétés supplémentaires


\vec {X}.(\vec {X}\wedge \vec {Y})=\vec {Y}.(\vec {X}\wedge \vec {Y})=0

\vec {X} \wedge(\vec {Y}\wedge \vec {Z})=(\vec {X}.\vec {Z}).\vec {Y}-(\vec {X}.\vec {Y}).\vec {Z}

\vec {X}.(\vec {Y}\wedge \vec {Z})=(\vec {X}\wedge \vec {Y}). \vec {Z}

\vec {X}.\vec {X}= \vec {0}

||\vec {X}\wedge \vec {Y}||^2=(( \vec {X}\wedge \vec {Y})\wedge \vec {X}).\vec {Y}   

\vec {X} \wedge(\vec {Y}\wedge \vec {Z})+\vec {Y} \wedge(\vec {Z}\wedge \vec {X})+\vec {Z} \wedge(\vec {X}\wedge \vec {Y})= \vec {0}

(\vec {A}\wedge \vec {B})+(\vec {C}\wedge \vec {D})=(\vec {A}.\vec{C}).(\vec {B}.\vec{D})-(\vec {B}.\vec{C}).(\vec {A}.\vec{D})

_____Vecteurs non nuls

dans tout ce qui suit les vecteurs \vec {X} et  \vec {Y}   sont non nuls  


alors dans ce cas on vérifie \vec {X}^2.\vec {Y}^2\neq 0  


Soient deux vecteurs non nuls \vec {X}\neq \vec {0}   et  \vec {Y}\neq \vec {0}  


alors il existe \varphi selon 0 \leq \varphi \leq 180°

cet angle représente l'angle formé par deux vecteurs non nuls


tel que \vec {X}.\vec {Y}=||\vec{X}||.||\vec{Y}||.cos(\varphi)

de plus on vérifie alors ||\vec {X}\wedge \vec {Y}||=||\vec{X}||.||\vec{Y}||.sin(\varphi)

||\vec {X}\wedge \vec {Y}||^2=\vec{X}^2.\vec{Y}^2-(\vec{X}.\vec{Y})^2

mais aussi on vérifie ||\vec {X}*\vec {Y}||=\sqrt {\frac{\vec {X}^2.\vec {Y}^2-(\vec {X}.\vec {Y})^2}{\vec {X}^2}}= ||\vec {Y}||.sin(\varphi)

on vérifie

\varphi =arccos \begin {pmatrix}\frac {\vec {X}.\vec {Y}}{\sqrt {\vec {X}^2.\vec {Y}^2}}  \end {pmatrix}

cos(\varphi ) =\frac {\vec {X}.\vec {Y}}{\sqrt {\vec {X}^2.\vec {Y}^2}}

sin(\varphi ) =\sqrt {\frac {\vec {X}^2.\vec {Y}^2-(\vec {X}.\vec {Y})^2}{\vec {X}^2.\vec {Y}^2} }

de sorte que

lorsque \vec {X}.\vec {Y}=0 on obtiens  \varphi =90°

lorsque \vec {X}.\vec {Y}>0 on obtiens 0 \leq \varphi < 90°

lorsque \vec {X}.\vec {Y}<0 on obtiens 90 °< \varphi \leq 180°

Enfin et on va pouvoir passer à la résolution de ce fil

les deux vecteurs non nuls \vec {X}\neq \vec {0} et  \vec {Y}\neq \vec {0}   sont dits colinéaires si et seulement si

(\vec {X}.\vec {Y})^2=\vec {X}^2.\vec {Y}^2  

alors dans ce cas

*lorsque \vec {X}.\vec {Y}-\sqrt {\vec {X}^2.\vec {Y}^2}=0

alors dans ce cas les deux vecteurs non nuls  \vec {X}\neq \vec {0}   et  \vec {Y}\neq \vec {0}    ont mêmes direction et sens

*lorsque \vec {X}.\vec {Y}+\sqrt {\vec {X}^2.\vec {Y}^2}=0

alors dans ce cas les deux vecteurs non nuls  \vec {X}\neq \vec {0}   et  \vec {Y}\neq \vec {0}    ont mêmes direction mais de sens opposés


à présent on peut passer à la résolution de ce fil

Posté par
miellere : Intersection de deux sphères 30-10-13 à 23:22

Merci pour ce cours détaillé

Et bien , j'ai compris votre explication
lorsque je les voit comme ça j'imagine que tout est simple!

Posté par Profil amethystere : Intersection de deux sphères 30-10-13 à 23:32

de rien camarade Mielle!
ne t'inquiète pas la suite c'est la résolution de ce fil et c'est simple
vraiment le plus galère est passé
belle soirée Camarade
je posterai la solution de ton fil demain
là j'écoute de la zic
@+Camarade

Posté par
miellere : Intersection de deux sphères 31-10-13 à 09:06

Citation :
ne t'inquiète pas la suite c'est la résolution de ce fil et c'est simple

Je pense pas que c'est assez simple surtout que si on va prendre en considération qu'une articulation peut avoir trois degrés de liberté (une angle selon x, selon y et selon z)

Posté par Profil amethystere : Intersection de deux sphères 31-10-13 à 10:26

Bonjour Mielle
je parle de ce fil
intersection de deux sphères
c'est simple à présent
si je te dit par exemple \vec {V}*\vec {W}
tu consulte le dernier post comment ça se calcule
et en plus tu saura pourquoi

l'autre fil y a un truc à faire mais chaque chose en son temps
d'abord ce fil et ne t'inquiète pas
fait moi confiance Camarade
aujourd'huit je travaille pas bon c'est vrai cette nuit je me suis cassé la tête sans résultat sur un autre fil (j'avais envie de faire autre chose )
mais bon ce soir je m'occupe de ce fil
promis Camarade

Posté par
miellere : Intersection de deux sphères 31-10-13 à 10:37

en faite  pour ce fil j'ai trouvé une solution

j'ai fixé une coordonnée z de point , et j'ai trouvé les deux autre coordonnées
alors ce fil est résolu

Posté par Profil amethystere : Intersection de deux sphères 31-10-13 à 10:51

Mielle

d'accord passons à l'autre fil dans ce cas

vous allez vite mais bon...(si jamais vous changez d'avis je vous assure c'est rien je le faisait ce soir et c'était bon)

ce qui compte c'est que vous soyez satisfaite

Posté par
miellere : Intersection de deux sphères 31-10-13 à 11:16

dans votre proposition on va trouver une seule point ? et pas une cercle ?
si oui Ok , je veux savoir qu'elle est votre idée

Posté par Profil amethystere : Intersection de deux sphères 31-10-13 à 11:32

on va avoir l'ensemble de tous les points donc un cercle (sauf le cas où il s'agit de deux sphères en contact où là il n'y en a que un) Mielle

au fait j'ai commencé sur l'autre fil

cependant ce que je viens de dire sur l'autre fil sera utilisé ici aussi

dites moi si ce que j'ai dit sur l'autre fil c'est ok pour vous

je sais pas ?
  

Posté par Profil amethystere : Intersection de deux sphères 31-10-13 à 13:44

Mielle

je viens de terminer le fil Géométrie 3D angles si tu as des questions sur ce fil là ou des objections  on reste là bas sinon on viens ici terminer celui là qui est encore plus rapide à faire
mais on verra demain pour celui-ci car je suis un peu crevé là

belle soirée Camarade Mielle si je reviens pas entre temps

Posté par Profil amethystere : Intersection de deux sphères 01-11-13 à 07:17

Bonjour Mielle
avant de passer à la résolution de ton fil et pour completer le post précedent et t'aider sur ton autre fil par quelques explications

je te decris vaguement en lecture seule ces trois choses(la premiere n'est pas vague il faut que tu la réalise concrètement)

la premiere est d'appliquer le post précedent à des vecteurs du plan
donc à deux composantes uniquement \vec {V}=(v_1,v_2)  
là le produit vectoriel ne te sert pas mais pour le reste cela peut t'aider à visualiser en reportant sur un repere plan
produit par un scalaire,addition et produit scalaire
de plus l'opération \vec {V}\times \vec {W}   et si tes deux vecteurs sont non nuls l'operation \vec {V}* \vec {W}  

la seconde necessite quelques posts (tu peut ouvrir un fil :perspective centrale ou bien en parler ici une fois ton fil résolu) mais je te la décrit vaguement en lecture seule -prend ton temps- voilà: Si tu fais du dessein (là c'est pour une visualisation 3D j'ai trouvé un lien assez chouette simple dans sa conception mais qui pose un problème comme je te le dit plus loin cependant je te le recommande (il n'est pas de moi) donc à consulter



tu comprendra qu'une fois le carrelage virtuel (le carrelage est la projection d'un plan situé dans l'espace et orthogonal au plan de projection) effectué(il s'agit de placer sur un plan des point situé dans l'espace) on construit" les "cubes" pour situer sur le plan de projection tout objet projetable et situé dans l'espace

cependant le principe de la perspective centrale décrit ici n'est pas absolue et pire encore il n'est pas pratique car il n'est pas mathématiquement formel

il existe d'autres méthodes plus formelles et que je te conseille d'utiliser
cependant ce lien est bien fait et te permet de visualiser mentalement ce dont il s'agit ici
disons qu'en lecture seule ici afin de "visualiser mentalement" ce dont on parle

encore une fois le carrelage virtuel étant construit (il ne s'agit pas ici de le construire ce que j'entend par le mot "construire" c'est d'utiliser des transformations par des formulations mathématiques) donc on construit les "cubes" virtuels pour pouvoir situer sur le plan de projection tout objet projetable situé dans l'espace)projetable c'est à dire "visible"
si tu dispose d'un ensemble de points que tu désire projeter sur ton plan de projection il y a une formulation mathematique qui tu dit si tel ou tel point est projetable ou pas (donc visible ou pas)

le principe de la construction du carrelage est basé sur le fait que les lignes parallèles au plan de projection lorsqu'elles sont projetées sur le plan de projection se rapprochent les une une des autres jusqu'à se confondre sur la ligne d'horizon du plan de projection

en fait la ligne d'horizon que l'on va nommer l_{\infty} représente la projection d'une ligne parallele l'on va nommer L_{\infty} au plan de projection et située à l'infini

lorsque tu considere ton plan de projection (il s'agit habituellement d'un  segment rectangle de plan)prend pour convention de faire en sorte que le repere de ce plan soit definit par O=(0,0) est le point origine du repere et situé au coin inferieur en bas à gauche de ton plan

l'abscisse est constituée par la droite horizontale inférieure de ton plan et l'ordonnée est constituée par la droite verticale situé à gauche de ton plan  

ton repere ainsi construit alors si tu nomme par E=\{P_1,P_2,...   \} est l'ensemble de tous tes points situés dans l'espace (donc les points possèdent trois composantes P_j=(p_1,p_2,p_3) et projetables sur ton plan de projection (donc uniquement ceux là et pas tous les points possibles de l'espace) alors lorsqu'ils sont projetés sur ton plan de projection

alors à tout point P_j \in E donc à tout point appartenant à E correspond un point Q_j=(q_1,q_2) qui est la projection de ce point  P_j   sur ton plan de projection

on va nommer  l'ensemble   F=\{Q_1,Q_2,...   \} est l'ensemble des points  P_j \in E qui sont projetés sur ton plan de projection

cette projection est une bijection f(P_j)=Q_j \in F

si tu contruit ton repere 2D de ton plan de projection decrit comme precedemment alors obligatoirement

pour tout point Q_j=(q_1,q_2) on obtiens q_1\geq 0 et q_2\geq 0

il est necessaire d'ouvrir un fil ou parler de cela plus tard ici il s'agit uniquement de decrire vaguement afin de "visualiser mentalement"

la troisième chose une fois les deux choses premières choses acquises est de se donner la possibilitée mathématique de pouvoir changer de repere

car jusque là tout ce qu'on a vu est la description de points sur un seul et unique repere

ce repere est dans l'espace le repere canonique que je ne decris pas ici formellement

lorsque tu dit:" je dispose des coordonnée d'un point" et cela sans autre précision on pense d'emblée que ces coordonnées sont definies sur ce repere canonique

voilà à présent il reste à terminer ce fil puis on passera si tu le désire à la projection centrale

entre temps si tu a des questions n'hesite pas

je n'ai pas trop le temps là pour terminer ce fil là je te l'envois plus tard


Rechercher
Menu
Espace membre
51 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !