C} 
Annuler
connectez vous
- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Autres ressourcesTopics traitant de Autres ressources [tout]Lister tous les topics de mathématiques
Niveau terminale
Isometrie2
Posté par theengineer
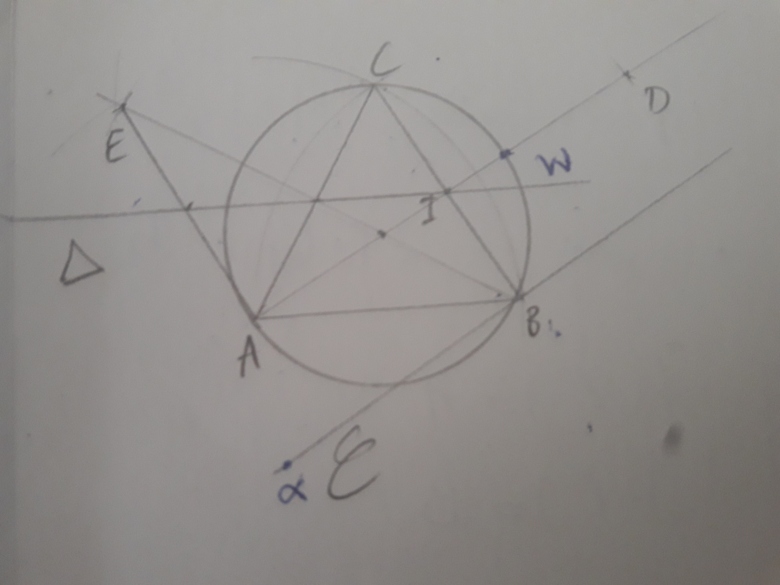
Bonjour, ABC equilateral direct inscrit dans un cercle C. I milieu de [BC] et E symétrique de B par rapport a (AC) .
F=R(A,
/3)
G=r(w,-2/3)
Et M un point variant tel que f(M)=M' et g(M)=M".
On demande de montrer que montrer que M'M" passe par un point fixe lorsque M varie , ce que je n ai pas arrivé a démontré, et merci d avance
Bonjour,
recopier par citation inutile le même message à l'identique ne va pas permettre d'avancer pour savoir ce que diable pourrait bien être "w" !!
Bonjour,
Citation :
M un point variant tel que f(M)=M' et g(M)=M"
M un point variant tel que f(M)=M' et g(M)=M"
M est un point variant du plan ? d'une droite ? d'un segment ? (...)
Ne serait-ce pas plutôt
M point variant du plan .. et voila tt l enoncé de l exercice
ABC equilateral direct inscrit dans un cercle C. I milieu de [BC] et E symétrique de B par rapport a (AC) .
F=T(vecteur BC)°r(B,/3)
G=S(centre I)°r(B,/3)
1) déterminer la nature de f et ses éléments caractéristiques
2)a)déterminer g(B)
b)montrer que g une rotation dont on précisera l angle
c)soit w centre de g. Montrer que w appartient C et construire w.
3)pour tt point M du plan distinct de C on note M'=f(M) et M"=g(M) . Montrer que la droite M'M" passe par un point fixe lorsque M varie
ah bein voila
avec l'énonce entier c'est bien plus clair !!
les composantes initiales dans l'énoncé (le vrai) de f et g sont bien plus utiles que f et g "simplifiées" des question d'avant !
on y voit bien plus clair en virant tout ce qui ne sert à rien à cette question.
caractériser la transformation M' --> M --> M''
???
c'est pourtant on ne peut plus clair
seul ce que j'ai mis sur ma figure est utile pour la question 3
aucun des points A, E, W etc n'est utile.
seules les définitions de f et g sont utiles, aucune des questions précédentes ne l'est.
f = T(vecteur BC) ° r(B,/3),
composition de la rotation M 
M1 et de la translation M1 M'
g = S(centre I) ° r(B,/3)
composition de la rotation M M1 et de la symétrie M1 M''
j'ai donc fait figurer explicitement ces compositions et ce point M1 sur ma figure
je te dis que pour résoudre cette question 3 il faut considérer la transformation M' M''
et que cette transformation est la composition de M' M et de M M''
M' M est la transformation inverse de M M'
qui d'après l'énoncé est f
quel est l'inverse de cette transformation ?
M M'' est directement la tansformation g
donc M' M'' est la composition de f-1 suivie de g
ça donne quoi cette composition de f-1 et de g ?
indice :
en regardant la figure on peut émettre la conjecture que ce serait la symétrie de centre B ** edit : de centre C **
...
il ne reste qu'à prouver cette conjecture.
c'est à dire à simplifier au maximum g ° f-1 pour espérer aboutir à S(B) **edit à S(C) **