Inscription / Connexion Nouveau Sujet
Joute n°33 : Le triangle partagé
Bonjour à tous,
Je vous propose de réviser un peu votre géométrie.
On découpe le triangle ABC de surface égale à 240 unités de façon à ce que AB/AE = 3 et AC/AD = 2 (le dessin n'est pas à l'échelle) :
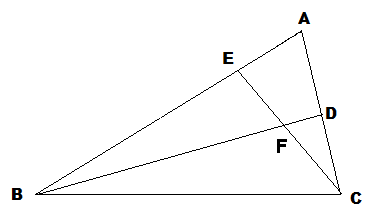
Question : quelle est l'aire de chacune des 4 parcelles ainsi découpées ?
Si besoin, vous donnerez les résultats arrondis au centième le plus proche.
 Bonjour godefroy,
Bonjour godefroy,
je propose :
L'aire de ADFE est 56.
L'aire de DCF est 24.
L'aire de FCB est 96.
L'aire de EFB est 64.
Merci.
 Bonjour, je trouve que AEFD a une aire de 56.00 (bizarre, je ne trouve que des valeurs entières), que DFC a une aire de 24.00, que FBC a une aire de 96.00 et que BFE a une aire de 64.00.
Bonjour, je trouve que AEFD a une aire de 56.00 (bizarre, je ne trouve que des valeurs entières), que DFC a une aire de 24.00, que FBC a une aire de 96.00 et que BFE a une aire de 64.00.
 Re-bonjour,
Re-bonjour,
Pas besoin de grandes notions de géométrie pour résoudre cette énigme... 
Si on trace le segment AF, le triangle ABC est séparé en 5 petits triangles selon :
A partir de là, la seule chose à savoir vient de la formule de la surface d'un triangle :
Si deux triangles ont une même hauteur, ils ont des surfaces proportionnelles à leurs bases.
Alors :
- triangles AFD et CFD :
c / d = AD / DC = 1 => d = c
- triangles BFE et AFE :
a / b = BE / EA = 2 => a = 2b
- triangles ABD et CBD :
(a+b+c) / (d+e) = AD / DC = 1 => d+e = a+b+c => e = 3b
- triangles BCE et ACE :
(a+e) / (b+c+d) = BE / EA = 2 => 2(b+c+d) = a+e => 4c = 3b
Et, puisqu'on connait la surface totale du triangle ABC :
a+b+c+d+e = 240 => 6b+2c = 10c = 240 => c = 24
Finalement :
4c = 3b => b = 32 => ADFE = b+c = 56
e = 3b => e = 96 => BCF = e = 96
a = 2b => a = 64 => BEF = a = 64
d = c => d = 24 => CDF = d = 24
 Bonjour,
Bonjour,
Notons l'aire du morceau de quadrilatère AEFD S1, du triangle DFC S2, du triangle BFC S3, et du triangle EFB S3.
Nous avons alors
S1+S2+S3+S4=240
S4+S2=80
S3+S1=160
S1+S2=120
S1+S4=120
En résolvant ce système on a
S1=80
S2=40
S3=80
S4=40
Merci pour l'énigme 
 Bonjour Godefroy.
Bonjour Godefroy.
aire de BEF = 64
aire de AEFD = 56
aire de BFC = 96
aire de DFC = 24
Désignons ces aires respectivement par a, b, c et d.
a+b = c+d = 120
b+c = 80
[AF) rencontre [BC] en G.
D'après le théorème de Céva, CG = CB/3.
AGC = FGC + FDC + AFD = ABC/3
c/3 + 2d = 80
c+d = 120
c = 96; d = 24
BAF = BAD - AFD = 120-d = 96
BEF = BAF * 2/3 = 64; a = 64
b = 120-a = 56; on a aussi b = AEF + AFD = BAF/3 + d = 32+24 = 56
 De la plus petite à la plus grande :
De la plus petite à la plus grande :
24,56,64 et 96 unités d'aires
La somme des deux plus petites fait 80, et la somme des deux plus grandes fait 160, vu la position de E.
La somme de la plus petite et de la plus grande est égale à la somme des deux autres, et à 120, vu la position de D.
La plus grande fait 4 fois la plus petite, vu la position de F sur [BD] (obtenue grâce à des barycentres)

 Bonjour Godefroy,
Bonjour Godefroy,
AEFD: 56,62 par défaut
EBF: 66,49 par défaut
BFC: 93,51 par excès
FCD: 23,38 par excès
Merci pour la joute.
 Bonsoir
Bonsoir
En espérant ne pas avoir fait d'erreur de calcul comme dans la joute 31 je propose en unités d'aire
aire BFC = 96: aire BEF = 64 ; aire DFC = 24 et aire AEFD = 56
A+
 Bonsoir godefroy_lehardi
Bonsoir godefroy_lehardi
aire du triangle DFC = 24 unités
aire du triangle BFC = 96 unités
aire du triangle BEF = 64 unités
aire du quadrilatère AEFD = 56 unités
ce qui est vrai pour un triangle quelconque est vrai aussi pour un triangle
particulier, j'ai pris ABC équilatéral (la réciproque est fausse)
à partir de là on peut calculer le côté, la hauteur, les angles, les surfaces, etc...
merci pour l'énigme
 Si x= aire BEF y= aire EFDA z= aire BFC et t= aire FDC,
Si x= aire BEF y= aire EFDA z= aire BFC et t= aire FDC,
en utilisant plusieurs fois la formule de l'aire= base*hauteur/2
et les rapports donnés dans l'énoncé, il vient que
(car EFDA se décompose en deux triangles AEF et FAD ...)
En résolvant ce système, on tire que
x=64 y=56 z=96 et t=24.
 bonjour,
bonjour,
j'utilise le fait que
on en déduit facilement que
d'où:
sauf étourderie de ma part
merci pour ce petit problème
 bonjour,
bonjour,
voici la solution que je propose:
- triangle BFC = 96
- triangle FDC = 24
- triangle BEF = 64
- quadrilatère EADF = 56
en espérant faire mieux que pour les triangles des pirates...
 Bonjour
Bonjour  ,
,
Je trouve :
AireAEFD=56
AireEFB=64
AireFBC=96
AireFDC=24
Démo :
On introduit un rond (B, ,
, ) tel que
) tel que  soit colinéaire à
soit colinéaire à . Dans ce repère, les coordonnées des points sont :
B(0,0)
C(xC,0)
A(xA,yA)
E((2/3)xA,(2/3)yA)
D((xA+xC)/2,yA/2)
F(xF,yF).
En utilisant le déterminant : AireABC=240 (1/2)*dét(
(1/2)*dét()=240
 yAxC=480
yAxC=480
Alors AireBEC=AireEFB+AireFBC=(1/3)yAxC=160 (càd AireAEC=80)
De plus, la médiane (BD) sépare ABC en deux triangles de même aire. Donc AireABD=AireDBC=120.
On a donc un système de la forme (par exemple) :
x+y+z+w=240
y+z=80
z+w=120
avec x=AireEBF, y=AireAED, z=AireDFC et w=AireBFC.
Ainsi, il n'y a qu'à trouver une parcelle pour trouver toutes les autres. Pour cela, il nous faut exprimer F en fonction des coordonnées de A et de C.
F est l'intersection de (EC) et (BD), on peut donner les équations cartésiennes de ces droites :
(EC) : (-yE/(xC-xE))*x+(yExC)/(xC-xE)
(BD) : y=(yD/xD)*x
En résolvant le système, on tombe sur xF=(2/5)(xA+xC) et yF=(2/5)yA. C'est bon, on peut calculer w (par exemple) : w=(1/2)*dét()=(1/5)yAxC=96 et remonter le système.
En espérant ne pas avoir fait d'erreur de calcul,
@+
 Bonjour,
Bonjour,
Sauf erreur, les aires (en unités) sont respectivement :
a = ADFE = 56
b = DCF = 24
c = BCF = 96
d = BEF = 64
Explication :
a+d = b+c = 240/2 = 120
a+b = (c+d)/2 = 240/3 = 80
Et surtout :
d/c = EF/FC
EF/2 = FC/3
... qui conduit à d/2 = c/3
... qui conduit à la solution indiquée.
 Juste pour dire que j'ai oublié de mettre les valeurs absolues pour la formule de l'aire avec le déterminant (mais je les ai pas oubliées dans les calculs
Juste pour dire que j'ai oublié de mettre les valeurs absolues pour la formule de l'aire avec le déterminant (mais je les ai pas oubliées dans les calculs  donc je reste sur ma réponse).
donc je reste sur ma réponse).

Si l'aire de ABC est fixe (égale à 240), si la longueur BC est fixée, alors A se déplace sur une parallèle à BC (par exemple sur le dessin si BC=40 alors BG=12). E,D, F se déplacent également sur des parallèles à BC. L'aire BFC qui vaut BC.FH/2 est donc constante (puisque FH l'est). De même BFE est constante puisque égale à EBC - FBC et que ces deux aires sont constantes. On en déduit de proche en proche que les 4 aires que l'on recherche sont constantes quand A varie. Il ne suffit plus que de les calculer dans un cas particulier (par exemple quand A est en G, le repère est alors orthonormé et le calcul des aires est très simple).
On trouve Aire BFC = 96 ; Aire BFE=64 ; Aire FDC = 24 et Aire AEFD=56
 Bonjour Godefroy,
Bonjour Godefroy,
Je propose :
Aire BEF = 64 unités
Aire EADF = 56 unités
Aire DCF = 24 unités
Aire CBF = 96 unités
Merci pour l'énigme et ... à bientôt pour la suivante
 Bonjour godefroy_lehardi
Bonjour godefroy_lehardi
aire AEFD = 56 unités
aire EBF = 64 unités
aire BFC = 96 unités
aire CFD = 24 unités
 Bonjour bonjour
Bonjour bonjour 
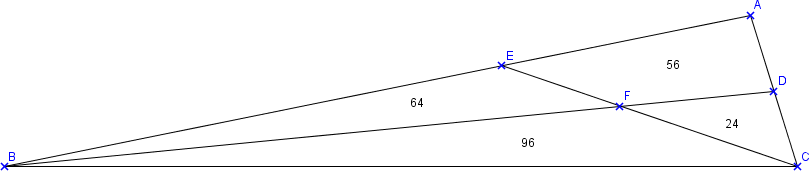
Voici la réponse que je propose (dans ma figure en bas).
Je me suis rapporté à un cas tout simple : j'ai considéré que le triangle ABC était un triangle rectangle en A. Ensuite j'ai considéré que AC=10 (pour avoir des résultats exacts par la suite). À partir de là je pouvais facilement en conclure que :
Et après j'ai bidouillé pour trouver les aires 
Mais ça m'a l'air tellement foireux mon histoire que ça sent le poisson 
Enfin tant pis j'aurais essayé 
Merci pour cette énigme, à bientôt ! 
 Bien voici ma méthode complète si ça intéresse quelqu'un (et si j'ai juste) :
Bien voici ma méthode complète si ça intéresse quelqu'un (et si j'ai juste) :
On doit avoir un triangle dont l'aire est de 240 unités. J'ai considéré que ABC est un triangle rectangle en A et que AC=10 (pour donc faciliter les calculs par la suite. L'aire doit être de 240 unités, donc :
Ensuite AB/AE=3 et AC/AD=2 donc :
Et la longueur de CB on s'en t
 Désolé bug -_-"
Désolé bug -_-"
Donc je disais la longueur de CB on s'en tape puisqu'on ne va jamais l'utiliser 
Bien maintenant qu'on a toutes les longueurs on va s'intéresser aux aires. Commençons par calculer l'aire de CAE :
Donc l'aire de CEB = 240-80 = 160cm²
L'aire de BAD=BDC 120cm²
Je finirais d'expliquer plus tard 
 Salut,
Salut,
Je trouve :
BEF = 64u
BFC = 96u
FDC = 24u
AEFD = 56u
avec AB = 48 et AC = 10, soit AE = 16 et AD = 5
merci @++
 Bonjour tout le monde
Bonjour tout le monde
Je propose ceci:
AEFD = 56 Unités
EBF = 64 Unités
BFC = 96 Unités
CFD = 24 Unités
Total = 240 Unités
 Bonjour godefroy_lehardi ,
Bonjour godefroy_lehardi ,
BEF = 64 unités
AEFD = 56 unités
BFC = 96 unités
CDF = 24 unités
Merci pour ce joute.
 Salut godefroy !
Salut godefroy !
Je trouve que les aires sont les suivantes :
Aire(AEFD) = 50 unités
Aire(FDC) = 30 unités
Aire(EFB) = 70 unités
Aire(FBC) = 90 unités
A+ et merci pour l'énigme.
 Lol, c'est vrai Louisa : une touche ne veut pas dire que le poisson est dans l'épuisette...
Lol, c'est vrai Louisa : une touche ne veut pas dire que le poisson est dans l'épuisette...
Mais bon il a le droit de rêver  ...
...
 Je sais, je vais à la pêche, j'ai des touches mais pas toujours de prises, des fois ça "lâche" ou "ça casse", mais il arrive que j'"accroche" bien !
Je sais, je vais à la pêche, j'ai des touches mais pas toujours de prises, des fois ça "lâche" ou "ça casse", mais il arrive que j'"accroche" bien ! 
Que c'est beau de rêver !!! 
 Bonjour
Bonjour
==> Rodival
J'ai fortement apprécié ta démonstration originale simple et claire
Moi je l'ai faite par l'analytique en prenant un triangle rectangle en A.
A+
Nombre de participations : 0
Temps de réponse moyen : 114:32:35.