Inscription / Connexion Nouveau Sujet
Joute n°36 : Un labyrinthe remarquable
Bonjour à tous,
Je vous propose de faire un petit tour dans ce labyrinthe un peu particulier.
Le départ se fait sur la case 1. On passe d'une case à une autre par un côté adjacent (donc pas en diagonale). On peut passer autant de fois qu'on veut sur chaque case.
Mais lorsqu'on a sauté de la case x à la case y, toutes les cases dont le numéro est un diviseur de la quantité |x²-y²| (valeur absolue de la différence des carrés) sont interdites pour le saut suivant (elles redeviennent éventuellement accessibles ensuite).
Par exemple, si on a sauté de 7 à 11, les cases 2, 3, 4, 6, 8, 9 et 12 sont alors interdites pour le saut suivant car |7²-11²| = 72.
En pratique, à partir de la case 11, on ne pourra donc pas aller sur la case 12. On ne peut aller qu'en 10 ou en 15, ou bien retourner en 7.
Pour le départ, il n'y a pas de condition. A partir de 1, on peut aller librement en 2 ou en 5.
Question : Quel est le chemin nécessitant un nombre minimal de sauts qui permet de passer au moins une fois sur chaque case ?
Donnez la suite des cases visitées dans l'ordre en commençant par 1.
S'il existe plusieurs solutions, une seule suffira.
Bonjour Godefroy
Je propose la suite de 19 sauts :
1, 2, 6, 7, 6, 2, 3, 4, 8, 7, 6, 5, 9, 10, 11, 12, 16, 15, 14, 13
Merci pour la joute 
Sans aucune certitude, je trouve une solution à 19 sauts (3 cases revisitées):
1-5-9-13-14-15-16-12-11-10-6-7-3-7-6-2-3-4-8.
Bonjour,
Dans l'ordre :
1 - 5 - 9 - 13 - 14 - 15 - 16 - 12 - 11 - 10 - 6 - 7 - 8 - 4 - 3 - 2
C'est forcément un chemin le plus court, peut-être le seul permettant de ne passer qu'une fois sur chaque case.
Les cases qui posent problème sont :
-la case 2 (on ne doit pas venir de 1)
-la case 3 (on ne doit pas venir de 7)
-la case 7 (on ne doit pas venir de 11)
Les déplacements horizontaux sont plus faciles, car la différence des carrés donne souvent sur un nombre premier. 
Pour les déplacements verticaux, la deuxième et la dernière colonne sont impossibles d'une traite, la première colonne est un passage obligé.
Merci pour le problème.
Bonsoir Godefroy,
Pour diminuer l'écriture, on note les cases:
123456789ABCDEFG
Le chemin proposé est de 17 sauts:
126A9 56234 87BCG FED
Merci pour la joute.
Bonjour
En 17 sauts ça marche ; pour le minimum ça reste à voir.
1 2 6 10 9 5 6 2 3 4 8 7 11 12 13 14 15 16
A+
Slt godefroid_lehardi, slt à tous
Je propose :
1 - 5 - 9 - 10 - 11 - 12 - 16
Merci pour la joute.
Bien à vous tous.
Bonjour.
x paire => x² paire
x impaire => x² impaire
donc on se déplace en colonne: différence de deux paire ou deux impaire = nombre paire
en ligne différence d'un paire et d'un impaire = un nombre impaire
Quand on se déplace en colonne, on peut ensuite aller vers un impaire
Quand on se déplace en ligne, on ensuite aller vers un paire.
Donc 1 -> 5 -> -> 9 -> 13 forcément ok.
13 -> 14 : 27 = 33 15 ne divise pas 27
14 -> 15 : impaire
15 -> 16 : impaire
16 -> 12 : paire
12 -> 11 : impaire
11 -> 10 : impaire
10 -> 6 : paire
6 -> 7 : impaire
7 -> 8 : impaire
8 -> 4 : paire
4 -> 3 : impaire
et 3 -> 2
Toute case visitée une fois, et un calcul à effectuer.
bonjour,
je suis un peu hésitante car je n'ai pas compris si il fallait uniquement passer au moins une fois par chaque case ou s'il fallait en plus sortir par la case 16 (j'ai pris la seconde interprétation)
voici donc le chemin suivi:
1-2
2-6
6-5
5-6
6-2
2-3
3-4
4-8
8-7
7-6
6-10
10-9
9-13
13-14
14-15
15-11
11-12
12-16
sauf étourderie, ce qui fait 18 sauts mais il y a sans doute mieux c'est à dire moins
merci pour cette joute
Bonjour Godefroy
Ce ne fut pas facile...
Je propose :
1 5 9 13 14 15 16 12 11 10 6 7 6 2 3 4 8
Un grand merci pour ce super challenge
A+
Bonjour,
Je propose le cheminement suivant, en 16 sauts :
1-5-9-13-14-15-16-12-11-10-6-7-6-2-3-4-8
Un cheminement "idéal" en 15 sauts permettrait de visiter toutes les cases sans passer deux fois sur une même case.
Mais un tel chemin n'existe pas, du fait principalement des contraintes d'accès aux cases 2, 3 et 4.
Il faut donc au moins 16 sauts, et dans ce cas, la solution proposée est bien minimale.
Merci pour l'énigme .
C'est plus joli en image...
La case 6 est la seule parcourue deux fois...
1-5-9-13-14-15-16-12-11-10-6-7-6-2-3-4-8
Bonjour et merci pour cette remarquable joute,
Au moins une solution: un chemin en 17 segments
1-2-6-5-9-13-14-15-16-12-11-10-6-7-3-7-8-4.
Ci-dessous une image correspondante:
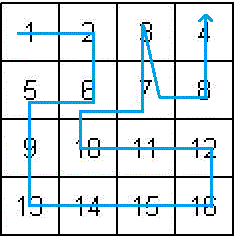
Bonjour godefroy_lehardi ,
Je propose le chemin :
1-5-9-13-14-15-16-12-11-10-9-5-6-2-3-4-8-7
Merci pour ce joute.
Salut Godefroy,
Il semble que tu ne comptes pas 1 au nombre des diviseurs d'un entier quelconque (je ne sais d'ailleurss pzas trop si cela aurait changé quelque chose) ?
Ceci dit, le chemin le plus court que j'aie pu trouver, avec 16 sauts, est : 1 - 5 - 9 - 13 - 14 - 15 - 16 - 12 - 11 - 10 - 6 - 7 - 6 - 2 - 3 - 4 - 8
Bonjour,
Je ne trouve pas mieux que la séquence suivante :
1 5 9 13 14 15 16 12 11 10 6 7 6 2 3 4 8
soit un chemin avec une seule case "doublée", le 6.
merci et à bientôt !
Modification :
1 - 5 - 9 - 13 - 14 - 15 - 16 - 12 - 11 - 10 - 6 - 7 - 8 - 4 - 8 - 7 - 6 - 5 - 6 - 2 - 3 - 4.
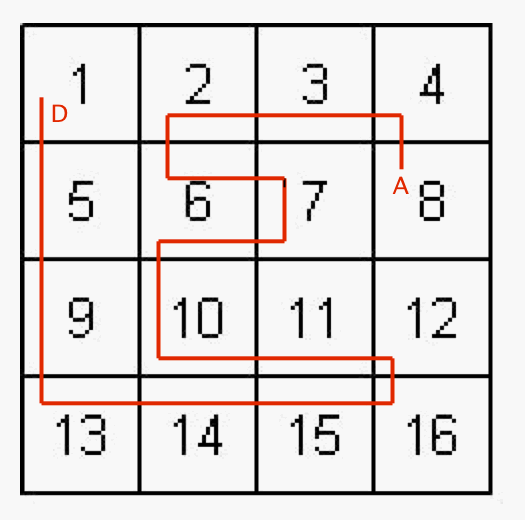
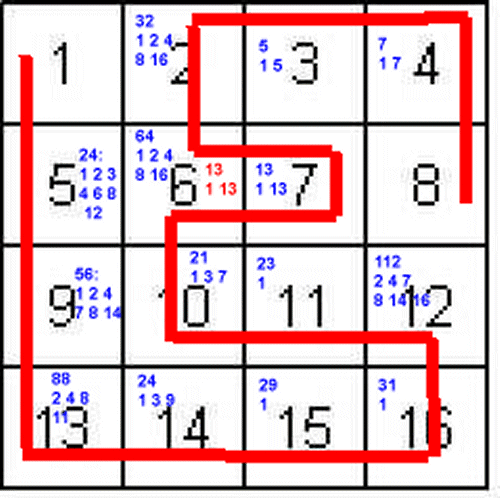
Clôture de l'énigme :
Beaucoup d'égarés dans ce labyrinthe ! 
J'espère que vous passez de bonnes vacances.
Et ne vous inquiétez pas, les énigmes continuent pendant le mois d'août ! 
à tous ceux qui ont trouvé...
Nombre de participations : 0
0,00 %0,00 %
0Temps de réponse moyen : 111:11:17.
Annuler
connectez vous