Inscription / Connexion Nouveau Sujet
Joute n°55 : Le code secret
Bonjour à tous,
Quand je me connecte sur le site de ma banque, je dois fournir un code secret en cliquant sur une grille dont voici quelques exemples ci-dessous.
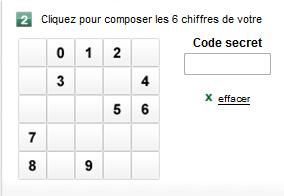


Les chiffres de 0 à 9 y sont inscrits une seule fois chacun de façon aléatoire, mais néanmoins dans l'ordre, selon le sens de lecture habituel (les lignes de haut en bas et les colonnes de gauche à droite).
On dira qu'une case est « paire » si la somme de ses numéros de ligne et de colonne est un nombre pair.
On dira qu'une case est « impaire » si la somme de ses numéros de ligne et de colonne est un nombre impair.
Par exemple, dans la première grille à gauche, la case contenant le 1 est située sur la première ligne et la troisième colonne. Elle est donc « paire » car 1 + 3 = 4.
Dans cet exemple, la parité du chiffre 1 ne correspond pas à la « parité » de la case où il se trouve.
Question : Quelle est la probabilité que chaque chiffre soit placé sur une case de même parité que lui ?
Je rappelle que le zéro est pair.
Vous donnerez la réponse sous forme de fraction rationnelle irréductible.
 Bonsoir,
Bonsoir,
Pour placer un chiffre donné (par exemple le 7), en supposant que tous les chiffres précédents satisfont aux conditions requises (bonne parité pour les chiffres 0 à 6, et possibilité de placer encore les chiffres restants), on a toujours exactement une chance sur deux de trouver une case ayant la bonne parité.
une chance sur deux d'une chance sur deux d'une chance sur deux... on trouve donc une proba de 1/1024.
Merci beaucoup pour la joute !
 Bonsoir,
Bonsoir,
j'ai probablement c'est le mot approprié, je crois raté un truc... car j'attribuerai bien 2* à cette joute !
Si l'on transforme la grille en une bande de 25 cases, le but est de répartir dans l'ordre les chiffres de 0 à 9 (en tenant compte de la parité),
soit en inversant le problème de répartir, dans l'ordre, certaines des 25 cases ou nombres dans une bande de 10 cases (de 0 à 9).
Je trouve alors 19448/25C10 i.e. 19448/3268760, soit une fraction irréductible de .
Merci pour cette joute.
 Bonjour,
Bonjour,
personnellement, je pense que chaque chiffre a une probabilité de 8/25 d'être placé sur une case de même parité que lui
 héhé ! et un poiscaille ! voilà ce que c'est de vouloir répondre trop vite ! surtout en matière de dénombrement ...
héhé ! et un poiscaille ! voilà ce que c'est de vouloir répondre trop vite ! surtout en matière de dénombrement ...
bon allez, je pense que c'est plutôt 13/2185
mm
 Bonjour Godefroy.
Bonjour Godefroy.
13/148580 (un peu moins de un dix millième)
(25*24*23*22*21*20*19*18*16)/(13*12*11*10*9*8*7*6*5*4) = 1/(2²*5*13-1*17*19*23)
 J'ai confondu chaque chiffre dans sa parité et chaque chiffre dans une case paire.
J'ai confondu chaque chiffre dans sa parité et chaque chiffre dans une case paire.
Ma réponse aurait dû être 11583/37145 (un peu moins de un tiers).
[(13*12*11*10*9)*(12*11*10*9*8)*(1*2*3*4*5*6*7*8*9*10)]/[25*24*23*22*21*20*19*18*17*16)*(1*2*3*4*5)*(1*2*3*4*5)]
= (217*310*54*7*11²*13)/(217*36*55*7*11*17*19*23)
= (34*11*13)/(5*17*19*23)
 On travaille sur une grille (5,5) ; notons n=5.
On travaille sur une grille (5,5) ; notons n=5.
La grille comporte n^2 cases et l'on doit y placer les nombres 0,1,...,2n-1 dans un certain ordre.
Déterminons d'abord le nombre de façons de remplir cette grille sans la condition de parité.
Mettons les lignes de la grille bout à bout. On obtient ainsi une grande ligne L de n^2 cases.
On est ramené à mettre sur cette ligne L les 2n nombres dans l'ordre croissant. Cela revient
à choisir 2n cases parmi n^2 cases. Le nombre de solutions est donc binomial(n^2,2n), c-à-d pour n=5,
binomial(25,10) = 3268760.
Déterminons maintenant le nombre de façons de remplir la grille avec la condition de parité.
Notons que si l'on indexe de 0 à n^2-1 les cases de la ligne L, la parité d'une case de L
(issue de la parité de la case correspondante de la grille) est égale à la parité de son indice.
Du moins si n est impair, ce qui est le cas ici puisque n=5.
Généralisons et prenons une ligne L munie de m cases indexée de 0 à m-1 (avec m impair).
Soit un entier n tel que 2 <= 2n <= m. On veut mettre dans les cases de cette ligne les entiers
de 0 à 2n-1, dans l'ordre, l'entier devant avoir même parité que l'indice de la case où il se trouve.
Notons nbrSolutions(m,n) le nombre de façons de le faire.
On montre aisément que
nbrSolutions(m,1) = (m^2-1)/8
nbrSolutions(m,n) = sum(j=1,(m-1)/2,j*nbrGrilles(m-2*j,n-1));
Pour montrer cette relation de récurrence on place 0 et 1 dans les cases de L :
0 dans la case d'indice 2i-2
1 dans la case d'indice 2j-1
On doit avoir 1<=i<=j<=(m-1)/2, donc pour un j donné, i peut prendre j valeurs ( de 1 à j) ;
c'est ce qui explique le facteur j dans la sommation.
De la relation de récurrence on déduit que
nbrSolutions(25,5) = 19448
Finalement la probabilité cherchée est égale à 19448/3268760 = 13/2185 .
 Bonjour
Bonjour
Réponse : 13451 / 4707164
Commentaire: supposons que les cases de la grille sont numérotées de 1 à 36 dans le sens de lecture habituel comme indiqué dans l'énoncé.Si l'on interprète cet énoncé à la lettre,l'inscription du "0" n'est possible que si la case choisie de manière aléatoire a un numéro <28, sinon il sera impossible de placer les chiffres restants de 1 à 9. De la même manière, l'inscription du "1" n'est possible que si la case correspondante a un numéro <29,etc...La probabilité demandée est alors très compliquée à calculer car elle doit intégrer les cas où les 10 chiffres ne peuvent pas être tous inscrits.
Nous avons fait l'hypothèse que la probabilité demandée était en réalité une probabilité conditionnelle à savoir : sachant que la grille a pu être remplie avec 10 chiffres de 0 à 9 lus dans cet ordre,quelle est la probabilité que chaque chiffre soit placé sur une case de même parité que lui ?
Dès lors l'épreuve consiste à tirer 10 boules dans une urne contenant 36 boules numérotées de 1 à 36 selon des tirages exhaustifs, ce qui donne C(36,10) = 254 186 856 combinaisons possibles. Chacune de ces combinaisons qui a la même probabilité d'apparaître 1/254 186 856, donne une séquence ordonnée de 10 entiers distincts qui sont les numéros des cases où seront inscrits respectivement les chiffres 0,1,2,...,9.
Parmi ces 254 186 856 combinaisons possibles, on dénombre à l'aide d'un mini programme ad hoc 726 354 combinaisons dans lesquelles le premier chiffre "0" appartient à une case paire, le second "1" à une case impaire,etc...
D'où la probabilité demandée 726 354 / 254 186 856 = 13451 / 4 707 164.
 Salut godefroy_lehardi et merci pour cette énigme
Salut godefroy_lehardi et merci pour cette énigme 
Je trouve que la probabilité que chaque chiffre soit placé sur une case de même parité que lui est de .
Voici ma méthode
Quelle est la probabilité qu'un chiffre soit pair ? 1/2 bien sûr. Quelle est la probabilité pour qu'une case soit paire ? 1/2 encore une fois. Donc la probabilité pour qu'un chiffre soit placé sur une case qui soit de même parité que lui est de 1/2 également.
Or, il y a 10 chiffres. Donc la probabilité pour que tous les chiffres soient placés sur une case de même parité qu'eux est de
En espérant ne pas m'être trompé,
Gryfo.
 Bonjour,
Bonjour,
Je dirais que la probabilité est de . En effet, il y a 16 cases possibles pour le zéro, dont 8 qui correspondent au cas qui nous intéresse, soit 1 chance sur deux que le zéro soit sur une case de sa parité. Or si tel est le cas, il reste selon moi autant de cases paires qu'impaires donc 1 chance sur deux également pour le 1 et on remarque que si le 1 est sur une case impaire alors on retombe dans une configuration avec autant de cases paires que de cases impaires possibles pour le chiffre 2 etc..etc..
Clôture de l'énigme :
Je mérite moi aussi un  : j'avais mis une étoile à cette joute parce que j'avais cru trouver un raisonnement très simple mais qui s'est révélé inexact.
: j'avais mis une étoile à cette joute parce que j'avais cru trouver un raisonnement très simple mais qui s'est révélé inexact. 
Je présente mes excuses à tous ceux qui n'auraient pas approfondi leur réflexion au motif qu'il n'y avait qu'une seule étoile.
Cependant, je rappelle que cette information n'est là qu'à titre indicatif.
Combien de fois une énigme parait-elle évidente à certains et ardue à d'autres selon les connaissances mathématiques de chacun, la méthode et les outils employés, l'idée fulgurante ou la fatigue du moment ?
 OK, ma réponse n'a strictement rien à voir, et j'ai beau regarder les démonstrations de quelques uns, je ne comprend strictement rien et d'ailleurs je n'ai pas plus compris pourquoi j'ai eu faux
OK, ma réponse n'a strictement rien à voir, et j'ai beau regarder les démonstrations de quelques uns, je ne comprend strictement rien et d'ailleurs je n'ai pas plus compris pourquoi j'ai eu faux 
Bref...
Bonjour Gryfo,
Tu as répondu 1/1024 = 1/210.
Cette réponse serait bonne s'il y avait eu 10 tirages indépendants de probabilité 1/2.
Les trois exemples ci-dessous illustrent ce cas.
Exemple 1 :
Probabilité d'obtenir pile dix fois de suite en jouant à pile ou face,
avec une pièce non truquée.
Exemple 2 :
Probabilité de tirer dix boules noires de suite en tirant au sort (avec remise),
dans un sac contenant autant de boules noires que de boules d'une autre couleur.
Exemple 3 (plus proche de l'énoncé, en apparence) :
Probabilité d'obtenir dix cases de même parité que l'ordre du tirage,
en tirant (avec remise), dix cases parmi 24 numérotées de 1 à 24.
Dans cet exemple, la parité imposée est connue dès le tirage de chaque case :
impaire au premier tirage, puis paire au deuxième, puis impaire à nouveau, etc...
Et comme on s'autorise à tirer plusieurs fois la même case (tirage "avec remise"),
la proportion de cases paires et impaires disponibles reste toujours la même
et donc la probabilité reste de 1/2 à chaque fois.
Si le problème avait été posé ainsi, ta réponse aurait alors été bonne.
---
Mais le problème proposé est bien différent :
En effet, non seulement les tirages ne sont pas indépendants, mais ils sont même au contraire en très forte interaction.
Au moment de chaque tirage (sauf au dernier), tu ignores quel sera le rang final de la case sélectionnée.
Et ce rang final dépendra de tous les tirages réalisés jusqu'ici et de ceux restant à effectuer.
Le processus aléatoire qui est appliqué ici est décomposable en deux temps :
1er temps : tirage des dix cases (chaque case ayant les mêmes chances d'être tirées).
2ème temps : calcul du rang (et donc de la parité) pour chaque case tirée, parmi les dix tirées.
C'est principalement cette étape de "tri a posteriori" qui vient perturber ton hypothèse de calcul et qui la rend totalement innapplicable.
---
Imagine par exemple que tu tires 10 cases au hasard parmi dix :
Comme tu les ordonnes pour leur affecter un numéro d'ordre dans la grille,
tu vas te retrouver avec à chaque fois les chiffres 0 à 9 sélectionnés,
couvrant l'intégralité de la grille, et ayant une parité de rang parfaitement en adéquation !
Dans cet exemple, le hasard ne sert strictement plus à rien,
car il est intégralement réordonné par le calcul du rang des cases sélectionnées
(qui lui même détermine la parité du rang).
Au final la probabilité sera de 100% dans ce cas extrême !
---
La seule bonne manière de réaliser le calcul :
... c'est d'effectuer le rapport entre le nombre de cas favorables,
et le nombre de cas possibles auxquels peuvent conduire le tirage.
Dénombrer les cas possibles est facile :
Il s'agit simplement de C(25,10), choix de 10 cases parmi 25 cases possibles :
C(25,10) = 25! / (15! * 10!) = 3 268 760.
Dénombrer les cas favorables est en revanche très complexe :
C'est ce qui faisait la difficulté du problème, qui valait de fait au minimum trois étoiles.
Le nombre de cas favorables s'élève à 19 448.
masab a proposé une jolie démonstration par récurrence de ce nombre.
Pierre_D a par ailleurs indiqué que ce nombre vaut C(17,7).
J'indique plus bas une explication de ce résultat.
Mais dans tous les cas, ce qu'il faut comprendre c'est que la probabilité cherchée était :
p = cas favorables / cas possibles = 19 448 / 3 268 760 = 13 / 2185.
J'espère que tu vois un peu mieux à présent d'où vient ton erreur...

---
Explication du nombre de cas possibles = C(17,7) :
Appelons "parfaite" une suite de dix cases satisfaisant les conditions.
Deux termes consécutifs d'une suite parfaite peuvent se suivre,
ou alors être séparés par un nombre pair de cases.
Si l'on cumule tous les cases séparatrices,
le total doit être inférieur ou égal à 14
(25-10=15, ramené à 14, car forcément pair).
Si l'on divise chaque nombre de cases séparatrices par 2,
et qu'on ajoute artificiellement un 11 ème terme,
pour combler l'écart éventuel permettant d'atteindre 14...
... alors on s'aperçoit que le problème revient à dénombrer
toutes les suites de n=11 entiers dont la somme vaut exactement k=7.
Un tel nombre est connu et vaut :
C( n+k-1 ; k) = C(11+7-1 ; 7) = C(17 ; 7)
Résultat qu'avait annoncé Pierre_D.
D'autres ont peut-être trouvé d'autres méthodes de calcul...
... mais se sont forcément des méthodes de dénombrement.
J'espère que ça t'aura éclairé.
Le problème était complexe de toutes manières, et bien au dessus d'un niveau 2nde.
 Merci LeDino ; en fait j'étais arrivé à ce résultat par récurrence (pas celle de Masab, pour autant que je me souvienne), mais il faut reconnaître que ton utilisation d'un théorème "connu" est bien pratique. Bravo.
Merci LeDino ; en fait j'étais arrivé à ce résultat par récurrence (pas celle de Masab, pour autant que je me souvienne), mais il faut reconnaître que ton utilisation d'un théorème "connu" est bien pratique. Bravo.
 Bonjour,
Bonjour,
Quand on compare la magnifique démonstration de LeDino
à la simple étoile de l'énigme on reste rêveur,d'autant
plus que la langue française est si subtile que j'avais
compris:
"Combien chacun* des chiffres a de chances de se trouver
sur une case de sa parité ".
La réponse dans ce cas était 1/2.
*chaque = tous
Bonjour dpi,
Merci pour ton compliment  ...
...
Pour ce qui est de l'interprétation alternative de l'énoncé que tu proposes, avec un "chaque" qui devient "chacun", elle n'est pas réaliste malheureusement.
Parce qu'absolument rien n'indique que cette probabilité soit la même pour chacun des chiffres.
On peut même raisonnablement penser le contraire, car chaque case n'a pas la même contribution pour chaque chiffre.
Donc il te faudrait répondre par dix probabilités p0, p1, ... p9, correspondant à chacun des chiffres de 0 à 9.
Pour bien comprendre ça, n'oublies pas que lorsque tu considères le chiffre 4 par exemple...
... il n'a AUCUNE chance de se situer sur les cases 0, 1, 2 et 3
(parce qu'il faut bien "caser" les chiffres 0 à 3 à gauche du 4).
Il ne peut non plus se situer sur les cases 21 à 25 (même raison "à droite").
Et il a très peu de chance d'être dans les casees "latérales" de type 4, 5, 6 ou encore 18, 19, 20...
tout simplement parce que cela "confinerait" les chiffres plus petits (ou respectivement plus grands) dans un espace très réduit...
Le calcul des P0 à P9 est probablement très complexe à réaliser.
 Bonjour,
Bonjour,
Merci LeDino pour ta réponse.
Bien sûr que j'ai pris en compte l'impossibilité de
placer par exemple 0 après la 16° case ou le 9 avant la
10° .C'est justement cela qui m'a enncouragé à faire
un simulateur de placement et je te confirme que le
nombre de chiffres bien "parisés" ressort à 5 en moyenne
au bout de centaines de placements aléatoires.
Donc la démo 1/2 devrait se faire .....
Bonjour dpi,
Ton simulateur de placement est une idée intéressante.
Mais qui pour l'instant ne résout pas le problème posé.
Si ton simulateur revient à recenser les cases atteignables pour chaque chiffre considéré, alors celà ne suffit pas.
Car chaque case n'a pas la même probabilité d'être atteinte par le chiffre que tu considères.
Ton hypothèse de probabilité située à 1/2 pour chaque chiffre est très probablement fausse.
Et la démonstration du résultat réel, quel qu'il soit, est d'une très grande complexité.
Si tu veux faire un simulateur, il faut procéder comme suit :
1. Tirer aléatoirement 10 cases parmi 25, avec chances égales pour chaque case d'être tirée.
2. Pour les 10 cases ainsi sélectionnées, calcul de leur rang sur le clavier.
3. Evaluation de la règle de parité pour chaque case/chifre (et classement en 0 ou 1).
4. Sommation finale des cas favorables à l'événement dont tu cherches la probablité.
---
Et si tu y réfléchis bien, tu verras que l'étape qui brouille tout est l'étape 2 :
car c'est le rang de la case sélectionnée qui détermine le chiffre.
Et il est quasiment impossible de calculer la probabilté que tel chiffre apparaissent sur telle case,
car le processus qui conduit à avoir ce chiffre est très complexe
et en interdépendance avec toutes les cases tirées.
Je pense que tu as sous estimée la complexité liée au processus aboutissant aux rangs (et donc au chiffres), et que de ce fait, ton calcul est incomplet (et faux).
Complément pour toi dpi :
J'ai fait un simulateur, qui tire au sort les cases, puis les ordonne pour obtenir les dix chiffres.
En dénombrant pour chaque chiffre, les cas où la parité est respectée, je trouve sur 10,000 tirages de dix chiffres :
p0 ~ 62%
p1 ~ 53%
p2 à p7 ~ 50%
p8 = 1-p1 ~ 47% (logique par symétrie)
p9 = 1-p0 ~ 38% (...)
Conclusion :
Pour les chiffres du milieu, ton intuition est plutôt correcte
(même si la valeur exacte de 1/2 n'est pas prouvée et qu'elle est même d'autant moins probable).
Pour les chiffres extrêmes, les "effets de bord" jouent à fond et biaisent la valeur centrale de 1/2.
Remarque :
Pour te rejoindre sur un autre point, il semble "qu'en moyenne" sur l'ensemble des dix chiffres,
la probabilité soit effectivement centrée sur 1/2 (valeur proche de l'intuition).
D'où ce paradoxe :
La probabilité globale : P[0 et 1 et 2 ... et 9] qui vaut environ 0.6%
est six fois supérieure au produit des probabilités P0*P1* ... * P9 qui vaut environ 0.1%.
S'il y avait indépendance, alors il y aurait égalité.
L'interdépendance crée une "auto corrélation" positive, qui tire la probabilité d'ensemble vers le haut.
Cela revient à dire que les chiffres ont une petite tendance à avoir une parité appropriée "en même temps".
Lorsqu'une case comporte un chiffre avec la bonne parité, celà augmente les chance des autres cases sélectionnées d'avoir aussi un chiffre à parité conforme.
Ce cas illustre très bien le fait que l'hypothèse d'indépendance est capitale pour pouvoir calculer P(A et B) comme P(A) * P(B).
A la prochaine  .
.
Nombre de participations : 0
Temps de réponse moyen : 126:34:06.


