Inscription / Connexion Nouveau Sujet
Juste une petite question...
Bonjour,
J'aurais aimé savoir comment calculer l'aire d'un triangle quelconque sachant sont angle au sommet?
Merci
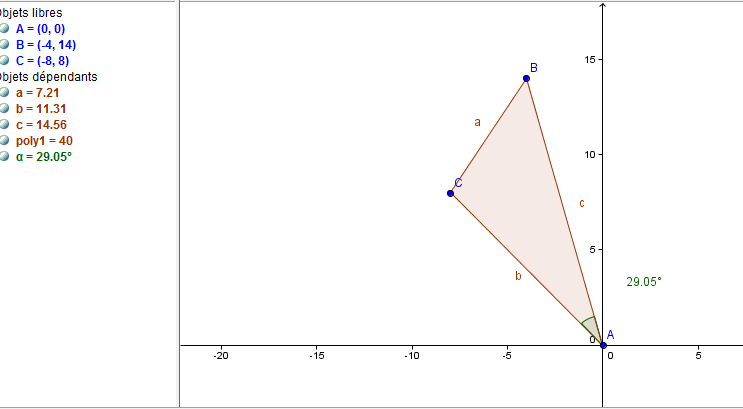
Je cherche à calculer l'air d'un triangle quelconque ABC sachant que A que l'on connait son angle calculé grace au produit scalaire (
) et on connait aussi les longueurs
Connaissant les côtés (a)(b)(c), tu as le
demi-périmètre ; p = (1/2)* (a + b+ c)
et l'Aire : A = racine[ p*(p-a)*(p-b)*(p-c) ] Formule de Héron .
52
Je pense que le mieux, c'est que tu prennes ta calculette . N'espère pas pouvoir simplifier ces mesures-là !
Bonjour,
Avec et
, l' aire est donnée par la formule:
et on peut calculer le sinus à partir du cosinus...
On trouve
bonjour,
si tu connais dans quel intervalle se trouve l'angle, applique le fait que sin²x + cos²x = 1
En coordonnées:
1) Chercher les coordonnées de pied de la hauteur issue de
du triangle
:
-On détermine une équation de la droite
-On écrit que les coordonnées de vérifient cette équation.
-On écrit que (puisque
)
-On résout ensuite le système formé par ces 2 équations pour obtenir les coordonnées de
2) On calcule les longueurs et
3) On a
On peut calculer directement à l' aide de cette formule:
Si l' équation d' une droite est et
, alors la distance de
à cette droite est donnée par:
Ici, on aurait
Annuler
connectez vous