Inscription / Connexion Nouveau Sujet
Le toboggan pour glaçons.


Mathias adore bricoler, quitte à fabriquer des choses qui ne servent à rien, juste pour s'amuser.
Il a donc projeté de réaliser un "toboggan pour glaçons" et a commencé à en dessiner le plan.
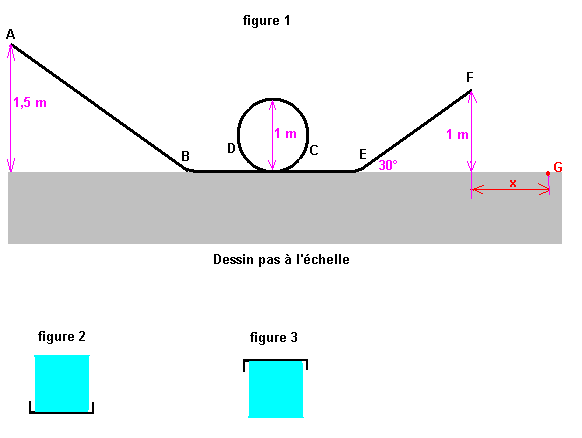
Son toboggan qui sera posé sur un sol horizontal, est constitué d'un U en plastique fin et lisse et il veut faire une piste de la forme de la figure 1.
Il lachera sans vitesse initiale un cube de glace au point A de la piste.
Mathias espère que le glaçon suivra la piste dans le trajet ABCDEF et puis décollera de la piste en F pour retomber au sol au point G.
Pour mieux comprendre, ce qui précède, la figure 2 montre un zoom d'une coupe de la piste en plastique et du glaçon lorsque le glaçon passe sur une partie horizontale de la piste.
La figure 3 montre un zoom d'une coupe de la piste en plastique et du glaçon lorsque le glaçon passe au point le plus haut de la boucle CD de la piste.
Avant de réaliser son projet, Mathias voudrait savoir si le glaçon peut effectuer la boucle sans tomber hors de la piste. Il voudrait aussi calculer la distance x qui repérera le point d'impact du glaçon sur le sol.
-----
Pour les calculs, le cube de glaçe pourra être considéré comme un point matériel de masse m (et donc les frottements sur la piste et dans l'air seront négligés).
On pourra aussi considérer que la piste est entière dans un plan vertical.
-----
Mathias a 2 questions:
- Le cube de glace peut-il franchir la boucle CD de la piste ?(justifier la réponse mathématiquement).
- Si le cube peut passer la boucle et dépasser le point F, alors donner la valeur de x à 1 cm près.
A titre d'informations:
La masse volumique de la glace est 900 kg/m³ et l'accélération de la pesanteur est 9,81 N/kg (ou m/s² pour celui qui préfère).
-----
Question subsidiaire (hors énigme)
Que deviendraient les résultats si le toboggan de Mathias était essayé sur la lune ?
-----
Bonne chance à tous. 
 Soit C' le haut du cercle.
Soit C' le haut du cercle.
Entre A et C', il n'y a aucun point placé plus haut que A. Donc la variation d'énergie potentielle entre tout point placé A et C' est négative.
Comme, entre tout points entre A et C', la variation d'énergie cinétique est égale à l'opposé de la variation d'énergie potentielle (car seule le poids travaille entre ces deux points), la variation d'énergie cinétique est positive, donc la vitesse ne s'annule jamais entre ces points (l'énergie cinétique initiale est nulle).
Donc le glaçon passera sans problème la boucle.
Pour les mêmes raison il passera le point F et la vitesse en ce point sera telle que 1/2 * m * v02 = m*g*(h1-h2). (variation énergie cinétique égal à opposé de variation énergie potentielle).
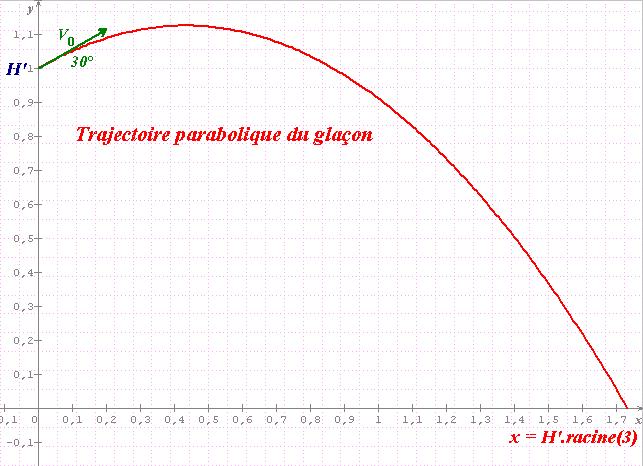
L'équation de la trajectoire d'un objet soumis uniquement à son poids et avec une vitesse initiale qui fait un angle a avec l'horizontale est (origine au départ du mouvement) :
Y = - 1/(2*v02 cos2a) * g * x2 +tan(a) * x
Si a =30° et y = -1 (axe orienté vers le haut)
On a x=1,0313 m = 103 cm



 Dis-donc c'est loin pour moi les formules de physique... Bon je vais essayer quand même.
Dis-donc c'est loin pour moi les formules de physique... Bon je vais essayer quand même.
Comme on néglige les frottements, il y a conservation de l'énergie. Au départ, la seule énegie est potentielle : E = m*g*h = 1,5 m*g
Au point le plus haut du "tourniquet", l'énergie totale sera égale à l'énergie potentielle (m*g*1), plus l'énergie cinétique 1/2 m*v2.
Donc en éliminant les m, on obtient la formule : g = v2
Au point le plus haut du tourniquet, la force centrifuge doit être supérieure au poids du glaçon, c'est à dire :
(m*v2)/r > m*g
Or ici r = 0,5, donc la force centrifuge = 2 m*v2 = 2 m*g > m*g
Ouf, ça tient !
Calculons à présent la distance x d'atterrissage.
Au point F, le glaçon a une vitesse V identique à celle qu'il avait en haut du tourniquet, comme son altitude est identique (1 m). On a donc V =  g.
g.
Par contre, cette vitesse se décomposera en une composante suivant l'axe horizontal : Vx = V cos 30° =  g * (
g * ( 3)/2
3)/2
et une composante suivant l'axe vertical : Vy = V sin 30° = 1/2  g
g
Une fois qu'il quitte le point F, le glaçon n'est plus soumis qu'à la seule accélération de la pesanteur, qui s'exerce suivant l'axe des y : A = - g
Il parcourt donc une parabole, dont l'équation selon l'axe des x est x = Vx t = ( 3)/2 (
3)/2 ( g)* t
g)* t
et selon l'axe des y : y = -1/2 g t2 + Vy t + 1
Le glaçon atteindra le sol quand y = 0, c'est à dire :
-1/2 g t2 + Vy t + 1 = 0
-1/2 g t2 + 1/2( g)*t + 1 = 0
g)*t + 1 = 0
Posons Y =  g* t, l'équation devient :
g* t, l'équation devient :
-Y2 + Y + 2 = 0 Une seule solution positive : Y = 2
Remplaçons dans l'équation des x :
x = ( 3)/2 * 2 =
3)/2 * 2 =  3 = 1,732 m = 173 cm
3 = 1,732 m = 173 cm
 Au fait .!! J'oubliais la question susbsidiaire.
Au fait .!! J'oubliais la question susbsidiaire.
Comme les résultats ne dépendent pas de g, la distance obtenue pour x sur la lune sera la même .. Simplement le mouvement sera ralenti (vitesses plus faibles).
 1- le glaçon effectuera la boucle sans "décrocher", si son accélération centrifuge au sommet de la boucle est supérieure à la pesanteur g.
1- le glaçon effectuera la boucle sans "décrocher", si son accélération centrifuge au sommet de la boucle est supérieure à la pesanteur g.
Si v est la vitesse au sommet de la boucle, pour une variation de hauteur de 0,5 depuis le départ sans vitesse initiale, la variation d'énergie cinétique donne v^2=g , soit une accélération centrifuge v^2/0.5=2g, qui est effectivement supérieure à g .
2- au point F, la vitesse est là encore telle que v^2=g elle se décompose en une vitesse horizontale u et une vitesse verticale w, u^2+w^2=v^2=g, avec, puisque l'angle est de 30°, u^2=3g/4 et w^2=g/4. Jusqu'au point G, la vitesse horizontale u reste constante, tandis que la vitesse verticale w' varie selon la distance horizontale x parcourue w'-w=gx/u, donc x=u(w'-w)/g.
Au point G, la vitesse est v' est selon le théorème de l'énergie cinétique v'^2=3g donc v'^2-v^2=2g soit w'^2-w^2=2g, donc w'^2=9g/4 et
x=(racine(3)/2)(3/2-1/2)=racine(3)/2=0,866m
Puisque l'on n'a jamais fait intervenir la valeur de g dans les calculs, les résultats seraient inchangés sur la lune...



 Le travail des forces autres que le poids est nul, car la réaction du plan est toujours perpendiculaire au déplacement.
Le travail des forces autres que le poids est nul, car la réaction du plan est toujours perpendiculaire au déplacement.
Donc entre deux points :
Delta d'énergie cinétique + Delta d'énergie potentielle = 0
Comme, sur tout le parcours entre tout points entre A et le haut de la boucle, la variation d'énergie potentielle entre l'origine et un point quelconque est négative, (puisque l'altitude est plus faible qu'à l'origine ), la variation d'énergie cinétique est positive.
Donc en aucun point la vitesse ne sera nulle, et le glaçon franchira la boucle CD.
On applique le même raisonnement pour montrer qu'il franchit le point F.
La vitesse en F sera 1/2 *m*vF2 = m*g*(h1-h2).
vF2 = 2*g*(hA-hF).
L'équation de la trajectoire d'un objet en chute libre avec un vitesse initiale vF qui fait un angle de 30° avec l'horizontale est, (en prenant l'origine du repère au départ du mouvement) :
y = [g/(2*vF2*cos230°) ]* x2 +tan(30°)*x.
Je prends y =-1 pour trouver la distance de l'impact avec le sol.
J'obtiens l'équation :
-2/3*x2+( 3)/3)*x +1 = 0
3)/3)*x +1 = 0
Ce qui donne x =  3, donc x=1,732 m = 173 cm.
3, donc x=1,732 m = 173 cm.
.
Sur la lune, rien de changé pour la trajectoire puisque l'équation ne dépend pas de g (vF2 est proportionnel à g qui se simplifie dans le coefficient de x2.
Simplement le mouvement se fera avec des vitesses plus faibles (au ralenti en quelque sorte) mais avec la même trajectoire.
 Bonjour,
Bonjour,
Hum... de la physique ou plutôt de la mécanique ! Alors là ça sent le  pour moi, m'enfin...
pour moi, m'enfin...
Après quelques recherches sur la toile pour me rafraîchir la mémoire sur ces notions, je tente le coup.
Etape1:
J'applique le théorème de l'énergie cinétique entre A et B: seul le poids travaille, l'action du plan étant perpendiculaire au plan (et les frottements et résistance étant négligés).
Il vient, (où
est la vitesse au point B.
D'où , soit
Etape2:
En l'absence de frottements, la vitesse est la même qu'en B à l'entrée de la boucle.
Etape3:
La bille passera-t-elle la boucle ?
Je note S le sommet de la boucle.
On utilise le théorème de l'énergie cinétique entre A et S (avec comme origine des altitudes celle du sol (le point B par exemple)) ou bien on écrit que l'énergie mécanique se conserve.
L'altitude de S doit être inférieure à celle de A, sinon S n'est pas atteint (on part sans vitesse de A).
Energie mécanique en A = énergie potentielle = mgh = 1,5mg
Energie mécanique en S =
où d=1 est le diamètre de la boucle
Ainsi, par conservation, , d'où :
i.e.
donc la vitesse au sommet n'est pas nulle et le glaçon passe...
Etape4:
Sauf erreur, inutile de calculer la vitesse à la sortie de la boucle à partir de la vitesse au sommet obtenue car la boucle est entière donc la symétrie parfaite (sans frottement); ainsi la vitesse à la sortie de la boucle est la même qu'en entrant donc toujours . Et de même, qu'à l'étape 2, la vitesse en E est encore la même, soit
.
Etape5:
De manière analogue à l'étape 1, avec vitesse initiale cette fois, on a:
d'où . Et
Etape6:(ouf!)
Le glaçon entre dans un mouvement parabolique avec pour vitesse initiale et un angle de 30°.
L'équation cartésienne du mouvement est donnée par la formule:
Le point d'impact est le point d'abscisse positive et de d'ordonnée y=-1, d'où l'équation :
Finalement la seule solution positive est x=
Ainsi, le point d'impact du glaçon sur le sol (avant de rebondir !  ) se situe à exactement
) se situe à exactement soit à environ
(de l'aplomb de F)
(le tout sans certitude cette fois... et sans utiliser la masse volumique de la glace ou la valeur de l'accélération de la pesanteur  )
)
Merci J-P pour ce casse-tête pour moi. L'énigme est sympa et bien emballée.
Question subsidiaire:
Les résultats seront identiques sur la lune (ou pour toute autre gravité) car celle-ci n'intervient pas dans la condition de passage de la boucle ni dans le calcul de la valeur de x (même si les vitesses changent).
Merci encore.



 J'ai oublié de répondre à la question subsidiaire.
J'ai oublié de répondre à la question subsidiaire.
Sur la lune, seule l'accélération de la pesanteur g change.
Cela ne change donc rien à la distance x, qui est indépendante de g (et de m), ni au fait que la glaçon peut franchir sans tomber l'épreuve du tourniquet, puisque les mêmes formules s'appliquent quelquesoit g.
Seule la vitesse prise par le glaçon sera moins importante, mais comme cela est compensé par une pesanteur moindre, cela n'influe pas sur la distance x.



 Bonjour,
Bonjour,
Essayons, bien que la physique remonte déjà à qques temps...
Réponses proposées :
1) le glaçon peut effectuer la boucle sans tomber hors de la piste.
2) x=173,2 cm par défaut x=racine(3) mètre
(Tentatives de) justifications :
1)
Notations : h hauteur du point A; H : sommet de la boucle situé à hauteur h', comme F.
En appliquant les conservations d'énergies (potentielle + cinétique) initiales et finales entre le point A et le point H, on a :
En A, énergie cinétique nulle (lâché sans vitesse initiale) + énergie potentielle=mgh => E = Ec + Ep = mgh
En H, énergie cinétique=mgh' + énergie cinétique=(1/2)mv² , v vitesse en H => E = Ec + Ep = mgh'+mv²/2
mgh = mgh'+mv²/2 => v²=2g(h-h')
Pour que le glaçon ne tombe pas en H, il faut que la force centrifuge (?) soit supérieure au poids :
C'est ici où je ne suis pas bien sûr et que le  peut surgir
peut surgir  : cette force est radiale et vaut (vaudrait) mv²/r avec r le rayon de la boucle : r = h'/2
: cette force est radiale et vaut (vaudrait) mv²/r avec r le rayon de la boucle : r = h'/2
soit, en valeurs absolues (norme) mv²/r > mg => r < v²/g or v²=2g(h-h') => r < 2(h-h') or r=h'/2 => h'<4(h-h') => h/h'>5/4
Comme h=1,5.h' ( 3/2>5/4 ), le glaçon restera plaqué contre le toboggan.
Par ailleurs, c'est en H que l'examen est le plus critique au cours du déplacement du glaçon dans la boucle.
Si le point A avait été à une hauteur inférieure à 1,25 m (pour une boucle de 1m), le glaçon aurait quitté la piste(*).
2)
Notation : repère O (=projection de F sur le sol ), axe Ox horizontal vers G, Oy vertical vers F; origine des temps : t=0 qd le glaçon est en F.
Je vais passer par les équations paramétriques temporelles du glaçon x(t) et y(t).
Le glaçon est soumis à la pesanteur -g tout au long de son "vol" et, à t=0, possède une vitesse vo donnée par :
En A : E = mgh ; en F : E = mgh'+mvo²/2 =>mgh=mgh'+mvo²/2 => vo=V[2g(h-h')] V pour racine.
A t=0 cette vitesse initiale est orientée selon l'axe du plan incliné (30° sur l'horizontale).
Les vecteurs sur Ox et Oy de cette vitesse initiale sont : vox=vo.cos(30) et voy=vo.sin(30)
Sur Oy, on a : y''=-g => y'=-gt+y'0 or pour t=0, y'0=vo.sin(30) => y'=-gt+vo.sin(30)
=> y(t)=-gt²/2+vo.sin(30).t+y0 or pour t=0, y0=h' => y(t)=-gt²/2+vo.sin(30).t+h'
Sur Ox, on a : x''=0 => x'=x'0 or pour t=0, x'0=vo.cos(30) => x'=vo.cos(30)
=> x(t)=vo.cos(30).t+x0 or pour t=0, x0=0 => x(t)=vo.cos(30).t
d'où t= x/(vo.cos(30)) que l'on remplace dans y(t) :
y(x)=-gx²/(2vo²cos²(30)) +tg(30).x+h' dans laquelle on remplace vo²=2g(h-h') :
y(x)=[-1/(4(h-h')cos²(30)]x²+tg(30).x+h' comme (1/cos² = 1+tg²) => y(x) = (-(1+tg²(30))/4(h-h'))x²+tg(30).x+h'
On cherche x>0 tel que y=0 => (-(1+tg²(30))/4(h-h'))x²+tg(30).x+h'=0 en appelant tg(30)=t
Delta = t²+(1+t²)h'/(h-h') = (ht²+h')/(h-h') >0
La solution positive à l'équation est x=2.( t + V[(ht²+h')/(h-h')] ).(h-h') / (1+t²)
Soit avec t=tg(30°)=1/V3 ; h=1,5 ; h'=1 => x=V3
3)
a priori, les deux expressions h/h' > 5/4 et y(x) = (-(1+tg²(30))/4(h-h'))x²+tg(30).x+h' étant indépendantes de g, je dirai que sur la lune on aurait les mêmes résultats.
Mais la seule main que je mettrai à couper serait celle de J-P  car je n'en suis pas certain du tout !
car je n'en suis pas certain du tout !
Pourquoi pas, aussi, une siouxerie sur la nature du glaçon (?) (quelle température sur la lune ?)...
Enfin, comme dirait notre PolytechMars et son chat,...
Merci pour l'énigme empoissonnée et, peut-être bien aussi, empoisonnée 
Philoux
Remarques complémentaires :
A moins que je ne me sois complètement planté, la masse volumique de la glace était superflue :
uniquement destinée à nous enduire "avec de l'erreur", J-P ? 
Pour forcer le trait, et peut-être nous faire douter encore plus, tu aurais dû nous donner un volume du cube de glace (de côté = 1cm, par exemple); ici, n'ayant que la masse volumique sans aucun volume, on est presque certain que la masse du glaçon n'intervient pas.
Il aurait pu être "intéressant", aussi, toujours pour piéger le quidam, de décider d'une fonte du glaçon selon une loi temporelle linéaire ( Volume=Vo(1-kt) )
In fine, introduire les frottements piste et air, soit sous forme constantes, soit sous forme proportionnelle à la vitesse...
* D'aucuns affirment que puisque la piste est entièrement dans un plan vertical, même si le glaçon n'est pas plaqué contre la piste au cours de la boucle, il retomberait dans celle-ci et la réponse serait toujours oui : de mauvaise foi, non ?
 salut J-P et bonjour à tous
salut J-P et bonjour à tous  :
:
Alors voila, je révise mon bac, mais comme ça se rapproche de ce qu'on peut avoir ... je tente ma chance .
1°) d'après le théorème de la variation de l'énergie cinétique :
<=>
<=>
<=>
<=>
le glaçon posséde donc une vitesse de 5,425 m/s lorsqu'il aborde le louping.
Le cube de glace étant considérer ici comme un point matériel, cela veut dire que son volume est très faible ( de l'ordre du milimètre cube ) . On en déduit donc que sa masse est elle aussi très faible.
Ainsi, vu que les frottements de la piste et de l'air sont exclut aucunes forces n'agit sur le glaçon.
Sa vitesse à l'arrivée étant très grande, il va donc pouvoir passer l'anneau sans problème ( comme le montre les figures 2 et 3 )
2°) Je vais supposer ici que la vitesse au poin E est la même qu'au point B ( ca qui doit être faux mais bon ...  )
)
Alors toujours d'après le théorème de la variation de l'énergie cinétique :
<=>
<=>
<=>
<=>
Maintenant, étudions ce qui se passe au point F. Le cube n'est soumis qu'a son poids, donc d'après la seconde loi de newton :
on a donc :
d'où :
et enfin :
On obtient donc l'équation de la trajectoire :
Il nous faut donc résoudre :
On résoud et on trouve finalement :
hors énigme : sur la lune, l'intensité de pesanteur est 6 fois plus faible. La vitesse va donc changer et g aussi.
Mais en refaisant les calculs, je trouve la même valeur ... 
Merci pour l'énigme et ne soit pas trop sévère avec moi ! 
@+ sur l'
lyonnais

slt
l'énergie mécanique en A est telle que :
or le solide est laché sans vitesse initiale donc en A v=0
l'énergie mécanique en B est telle que :
or en B h=0
Pour les calculs, le cube de glaçe pourra être considéré comme un point matériel de masse m (et donc les frottements sur la piste et dans l'air seront négligés).
>>il y a donc conservation de l'énergie mécanique entre les points A et B.
au point A :
au point B :
soit :
on en déduit qu'entre les points A et B la vitesse est de :
Pour les calculs, le cube de glaçe pourra être considéré comme un point matériel de masse m (et donc les frottements sur la piste et dans l'air seront négligés).
on en déduit qu'entre les points B et C la vitesse se conserve est vaut donc :
Pour les calculs, le cube de glaçe pourra être considéré comme un point matériel de masse m (et donc les frottements sur la piste et dans l'air seront négligés).
Pour savoir si le solide est capable d'effectuer la boucle nous devons calculer la valeur de la vitesse au sommet et conclure :
En C :
donc
En C' (hauteur maximale de la boucle) :
Donc
>>il y a conservation de l'énergie entre les points C et C'
on en déduit que comme nous connaissons la vitesse au point C au peut déduire la valeur de celle ci a l'altitude maximales c':
En C' (hauteur maximale de la boucle) :
donc
En D
donc
>>il y a conservation de l'énergie entre les points C' et D
on en déduit que C' et D la vitesse vaut :
On vérifie alors qu'entre A et D on a la meme valeur de la vitesse (aucun frottement n'influe sur le systeme
Pour les calculs, le cube de glaçe pourra être considéré comme un point matériel de masse m (et donc les frottements sur la piste et dans l'air seront négligés).
on en déduit qu'entre les points D et E la vitesse se conserve est vaut donc :
l'énergie mécanique en E est telle que :
or en E et h=0
l'énergie mécanique en F est telle que :
or en F et h=1
Pour les calculs, le cube de glaçe pourra être considéré comme un point matériel de masse m (et donc les frottements sur la piste et dans l'air seront négligés).
>>il y a donc conservation de l'énergie entre les points A et B.
soit :
on en déduit qu'entre les points E et F la vitesse est de :
On assimile le glacon à un point matériel M ;
il est lancé avec un vecteur vitesse de valeur
;
celui ci fait un angle a de 30° (alternes internes) avec l'horizontale ;
D'aprés la deuxième loi de Newton :
soit :
Les composantes de l'accélération dans le repère le repere considérer sont :
i.e.
i.e.
soit :
le point G verifie dans le repere les coordonées suivante :
on a donc :
et
on déduit donc que :
on pose alors : :
> equation du second degré que l'on resoud facilement :
la seule solution physique possible est
il doit surement y avoir des erreurs ... une correction ?
merci pour l'enigme trés interressante ...
@+
(Je n'ai pas le temps (BAC oblige) de pousser le raisonnement sur la dernière question mais je pense aprés petite verefication que sur la lune son tobbogan pour glacon marcherai (il vaut voir que la gravité est 6 fois moins faible sur la lune mais faute de tps ...))



 Bonjour à tous,
Bonjour à tous,
Voilà ma réponse aux deux questions deMathias :
- oui, il franchit sans probleme la boucle CD (la boucle peut faire jusqu'à 1.5m de diamètre)
explication : E= energie totale = Ep + Ec = mgz +1/2mv² référence = sol horizontal
on a donc E(1.5) = 1.5mg + 0 et E(1) = mg + 1/2mv²
Pas de frottement donc E(1.5)=E(1) donc 1/2mv²=1/2mg donc v²=g donc v n'est pas nulle
donc le glaçon ne décolle pas du support.
- Au point F, v²=g comme en haut de la boucle et angle = 30°
On trouve l'équation de la courbe :
Vect. Accélération ( 0 ; -g ) et par intégrations successives,
Vect. Vitesse ( v.cos30 ; -g.t+v.sin30 )
Vect. Distance ( v.cos30.t ; -1/2.t² + v.sin30.t + 1 ) = (x ;y)
On déduit de ce dernier vecteur, en remplaçant t, y = -1/2.g.x²/(v².cos²30) + tan30.x + 1
= -2/3.x² + x/V3 + 1
On cherche x quand y=0
Petite équation du second degré à résoudre, dans laquelle on ne garde que la solution positive :
On trouve 2,68 m.
Pour la question subsidiaire :
Dans la première question de Mathias, v²=g, donc sauf si g=0, v sera différent de zéro, donc
sur la Lune (g/=0) même résultat
On a vu que dans la seconde question de Mathias, g=v² se simplifiait, g «disparaît» de y, donc où que l'on soit, sur la Lune comme sur Mars ou Jupiter, si g/=0, on obtient aussi le même résultat.
Il faut juste retenir que la vitesse de décollage en F dépend de g
Si g diminue, v en F diminue mais la distance x sera la même car l'attraction sera moins forte.
See you later,
BABA
 Salut,
Salut,
Pour la première question, c'est facile, le point A étant situé plus haut que le haut de la boucle CD, l'énergie accumulée lors de la descente est supérieure à l'énergie nécessaire pour franchir la boucle.
Pour la deuxième question, c'est nettement plus dur, mais après de longs calculs certainement inutiles, je trouve :
x=3,11 m
(pour la lune, mes calculs me donnent 4,61 m)
PS : mes calculs sont sûrement faux



Bonjour à vous !
Sur la piste, le glaçon est soumis à 2 forces :
- son poids , vertical vers le bas
- la réacton du sol , perpendiculaire à la trajectoire
En l'absence de frottement, l'energie mécanique se conserve.
En A,
En B :
, donc
Au sommet du looping (S):
, donc
Deuxième loi de Newton :
,
En F :
, donc
Aprés F, le glaçon n'est soumis qu'à son poids.
 En vertu de la conservation de l'énergie, en tout point du circuit situé "en-dessous" de l'altitude initiale
En vertu de la conservation de l'énergie, en tout point du circuit situé "en-dessous" de l'altitude initiale la vitesse du point matériel vaut
Le glaçon franchit bien la boucle CD
Lorsqu'il décolle il est annimé d'une vitesse
Les composantes de la vitesse sont
En choisissant l'origine des temps à l'instant où le glaçon décolle, le glaçon touche le sol au bout d'un temps t solution positive de l'équation
on trouve
La distance vaut donc
Cette distance est indépendante de la constante gravitationnelle.



 Salut,
Salut,
La premiere question est simple c juste la conservation de l energie, sachant que l energie potentielle acquise est superieure a celle perdu dans le looping, puisqu il n y a pas de frottement donc le cube peut passer le looping.
Ensuite on applique le principe fondamental de la dynamique est on trouve qqch independant de la gravité :140cm. Qui dit independant de la gravité, donne la mm chose sur la lune...
A+
PS:Je la sens pas bien cette enigme

Enigme clôturée.
Bravo à Razibuszouzou, philoux et chrystelou qui ont réussi à utiliser le toboggan sans glisser hors de la piste. 
La plupart des autres participants ont approché de près la solution mais ont un peu dérapé sur le problème du passage de la boucle.
La plupart a montré que la vitesse au sommet de la boucle n'était pas nulle et en ont conclu que le glaçon pouvait donc passer la boucle.
Cette condition est nécessaire mais pas du tout suffisante.
Au sommet de la boucle, le glaçon a la piste au dessus de lui, pour qu'il puisse passer le sommet de la boucle, il faut donc que la force centrifuge sur le glaçon soit supérieure (au moins égale) au poids du glaçon, sinon badaboum.
Cette manière d'expliquer les choses a été parfaitement décrite par Razibuszouzou.
Si certains sont allergiques à la notion de force centrifuge (qui est indispensable si on étudie le passage de la boucle en se mettant dans un référentiel lié au glaçon), on peut étudier ce passage dans un référentiel galiléen.
Ici, on n'a plus besoin de la notion de force centrifuge mais la solution est alors un poil plus compliquée.
On peut par exemple calculer le début de la trajectoire du glaçon qui vient de passer le sommet de la boucle en imaginant la demi partie gauche de la piste formant la boucle enlevée, si le début de cette trajectoire sort du cercle de la piste, le glaçon peut alors franchir la boucle, si le début de cette trajectoire pénètre dans le cercle de la piste, c'est que le glaçon est incapable de franchir la boucle.
Cette approche (dans un référentiel Galiléen) est un peu plus dure (pas beaucoup) que l'approche dans un référentiel lié au glaçon faisant appel à la notion de force centrifuge.

Bonjour J-P,
franz trouve 1.73m et chrystelou aussi pourtant l'un a un poisson et l'autre un smiley.
D'où vient le problème?
A plus 
Salut clem clem.
chrystelou a un justification correcte du passage du glaçon au sommet de la boucle, franz et beaucoup d'autres pas.
Lire mon message précédent attentivement.




 Bonjour,
Bonjour,
Elle a fait mal, celle-là !
J'ai peur qu'en dérivant sur des notions de physique, vues qu'en 1° pour répondre à infophile, on restreigne grandement le nombre de participants.
ET même ceux qui s'y sont frottés sont tombés...du toboggan.
>clemclem
Sûrement parce que la question 1° n'est traitée par franz que par la vitesse...?
Philoux
Bonjour 
Bravo à tous ! 
Elle était dure cette enigme, je n'ai pas tout suivi  !
!
Mais je l'ai trouvée particulièrement interessante ! Il faudrait que j'appronfondisse ces notions de physique ! C'est super de pouvoir déterminer à quel endroit va retomber le glaçon...etc 
@+ sur l'
Kevin (Qui bloque sur l'enigme de Victor  )
)

 je savais bien que j'allais me prendre un poisson sur la première question.
je savais bien que j'allais me prendre un poisson sur la première question.
N'ayant jamais utiliser la force centrifuge ... 
Par contre, je suis assez fier d'avoir trouver les 1,73 m , ça prouve que j'arrive à appliquer mes formules de physique ! 
merci pour l'énigme

 Bouh-hou-hou et sniff !
Bouh-hou-hou et sniff !
Bon, ben j'ai pris une belle gamelle sur ce toboggan...
dire que j'était plutôt content d'être arrivé au bout (car, vraiment, la physique ce n'est pas mon truc... )
Bravo aux 3 qui ont esquivé la glissage et merci à philoux pour ses explications sur la force centrifuge (si A est à moins de 1m25 du sol le glaçon tombe...) qui m'ont permis d'un peu mieux comprendre et de constater que l'argument unique sur la vitesse ne tient pas.
Bravo à tous les paticipants à cette énigme !
Je n'ai plus aucune notion de physique, et donc cette énigme était au-dessus de mes capacités et pas l'ombre d'un espoir d'y arriver.
Merci pour les solutions détaillées, cela me perméttra de remettre quelques souvenirs en place.
Bonne continuation à tous.




 bonjour manpower,
bonjour manpower,
Juste un bémol à ce que j'ai écris : je ne suis pas expert et je ne suis pas complètement certain de mes assertions...
N'ayant pas (encore) été démenti, j'en déduis que ça ne doit pas être trop faux...
Ce pb continue de m'intéresser et, le temps de faire un dessin (sous word) pour exposer le pb et je reviens.
Bonjour à tous !
Philoux
 Pour moi, c'est sans regret.!!
Pour moi, c'est sans regret.!!
Avec une belle erreur de calcul (cos2(30°) = 1/3 !!!), je ne pouvais pas espérer avoir mon smiley.
J'ai traité le passage de la boucle un peu vite (comme d'habitude certains dirons,... mais on ne se change pas !).
Sinon j'ai trouvé qu'en partant d'un point A à 1,5 m , il fallait que le rayon de la boucle soit inférieur à 60 cm pour que çà tienne..
Bravo aux trois "futés" qui ne sont tombés pas dans le panneau.



 Bonjour NF2
Bonjour NF2
Bravo aux trois "futés" qui ne sont tombés pas dans le panneau
Pas si futés que ça NF2
Un coup de google pour rafraîchir les idées sur la notion de force centrifuge (j'avais tapé montagne russe) et je suis tombé sur :![]()
qui m'a bien aidé, je l'avoue !
Quant à ta remarque :
Sinon j'ai trouvé qu'en partant d'un point A à 1,5 m , il fallait que le rayon de la boucle soit inférieur à 60 cm pour que çà tienne,
ça corrobore tout à fait le "h/2r >5/4"
Une question cependant :
Si tu avais trouvé cette relation, entre h et r, tu avais donc écris la condition pour que le glaçon reste plaqué contre la piste ?
Alors que ta résolution de 13:49 ne parle que de vitesse non nulle au cours du déplacement ?
Y a qqchose que je ne saisi pas 
Philoux
 Je me suis mal exprimé !!!
Je me suis mal exprimé !!!
J'ai fait le calcul "après" la résolution de l'énigme ...
Je confirme : je me suis lamentablement planté sur le coup de la boucle .
Salut...





 Re-bonjour,
Re-bonjour,
Cette histoire de hauteur max m'a titillé.
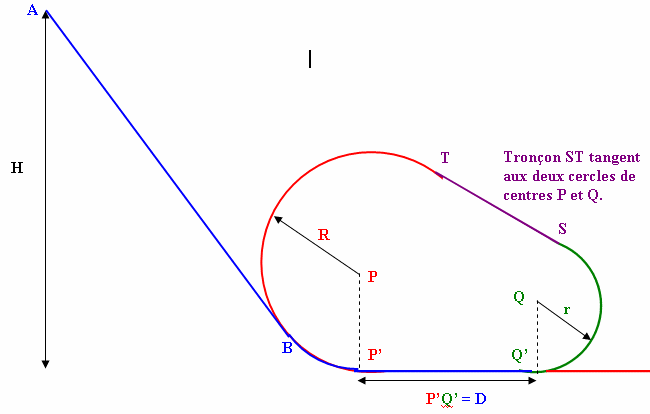
Supposons que notre Matthias désire faire une boucle composée de 2 cercles reliés par une piste rectiligne comme indiquée par le schéma ci-dessous.
Je me demande, en fait, si le glaçon suivra la piste (dans la partie haute de la boucle) pour des conditions identiques : H/2R > 5/4 ?
Est-ce que la distance D d'écartement des 2 cercles (D=P'Q') a une incidence ou pas ? (avec tjs comme hypothèse : pas de frottement) ?
Que se passe-t-il dans la partie rectiligne ST ?
Si d'aucuns ont des réponses... merci
Philoux



 Bien sûr que ça marche encore. S'il n'y a pas de frottements, il y a conservation de l'énergie mécanique.
Bien sûr que ça marche encore. S'il n'y a pas de frottements, il y a conservation de l'énergie mécanique.
Au départ il n'y a que de l'énergie potentielle E = m*g*H
Quel que soit le parcours que fait le glaçon avant, au point le plus haut du "tourniquet", L'énergie mécanique sera égale à l'énergie potentielle, plus l'énergie cinétique :
E = 2 m*g*R + 1/2 m*v2 = m*g*H
Cette équation permet de calculer la vitesse, comme précedemment.



 Merci Razibus,
Merci Razibus,
Cela signifierait donc que, sur le tronçon ST et au delà, le glaçon reste collé à la piste tant que la piste ne monte pas plus haut que 2R<4H/5 ?
Philoux



 Non non, excuse-moi, je n'avais pas bien compris ta question.
Non non, excuse-moi, je n'avais pas bien compris ta question.
Le glaçon quitte la piste et tombe dès que la trajectoire devient droite (au point S), car alors il n'y a plus de force centrifuge. La seule force qui s'exerce sur lui est la pesanteur.
On pourrait calculer sa trajectoire de la même façon que dans l'énigme ci-dessus, quand la piste s'arrête.
Nombre de participations : 0
Temps de réponse moyen : 22:29:05.