Bonjour

C'est une idée! J'espère que le topic ne deviendra pas un grand ramassis illisible, mais on peut toujours essayer!

Ma contribution:

Citation :
Le polynôme est réductible dans pour tout nombre premier , mais irréductible dans .

Je propose que dès qu'un membre poste un message dans ce topic, celui-ci doit être accompagné d'un exemple ou contre-exemple sus-cités.

Cela évitera d'avoir un topic "gruyère".

Citation :
Il existe des applications continues, bijectives, dont la réciproque n'est pas continue !

exemple : Je note le cercle unité de .

L'application de .

Bonjour.

Citation :
Le théorème des accroissements finis (ou de Rolle) n'est pas valable pour les fonctions à valeurs vectorielles, seule l'inégalité est valable.

L'application de dans est dérivable, vérifie , et pourtant

Dans le plan, on est pas obligé de marquer une pause pour revenir sur ses pas !

Deux contre-exemples sur les evns de dimension infinie.

Citation :
La boule unité de muni de la norme de la convergence uniforme n'est pas compacte.(cf Théorème de Riesz)

La suite n'a aucune valeur d'adhérence.

Citation :
L'espace muni de la norme , pour n'est pas complet.

En effet, si on pose
la suite de définie par est de Cauchy, mais n'est pas convergente.
(alors que les espaces de Lebesgue sont complets)

Bonjour Infophile.
Ton tracé ressemble à une fractale.
Une fonction représentée par une fractale serait telle partout indérivable ? La réciproque serait-elle vraie ?

Hey!

Il existe des fonctions R->R discontinues en tout point dont l'image de tout intervalle est encore un intervalle. (En clair, la propriété des valeurs intermédiaires ne caractérise pas du tout les fonctions continues).
De plus, toutes fonctions réelles s'écrit comme la somme de deux telles fonctions.

J'ai une question à la limite de la géographie,de la logique et des mathématiques (fractales):
QUELLE EST LA VERITABLE LONGUEUR DE COTES FRANCAISES
(marge d'erreur généreuse de 10 %)

Salut !

On peut construire une fonction définie sur , croissante, continue en tout point irrationnel, et discontinue ailleurs. (sur les rationnels)
En fait, on peut choisir les points de discontinuité comme on veut, du moment qu'ils sont en quantité dénombrable.

Pour répondre à dpi, je dirai volontiers que la longueur est infinie. (rien qu'une petite partie des côtes bretonnes suffit)

Bonjour

En dimension infinie on n'a en général pas ni

Citation :
Exemple : et . On prend comme produit scalaire et on montre alors que

Y en a quelques uns là : (désolé de faire la pub d'un autre forum ^^)

salut

Citation :
il existe une fonction continue sur   ,qui sur tout segment se prend aumoins une fois une valeur negative,postive et la valeur nulle

Ha! milton

Ca me parait suspect ton histoire, si on prend un point a où f(a)>0 par exemple, alors par continuité il existe un voisinage du point a sur lequel f reste strictement positive... il suffit de prendre un segment inclus dans celui-ci.

pouvez vous m'aidez a résoudre un probleme je suis en 4 eme .

salut info
si ca existe. je l'ai trouvé  en lisant un  cours sur la H-K integration ( sans le verifier bien sur )

Bonjour ,
N'étant qu'un simple terminale S j'ai un peu de mal à comprendre tout ce que vous postez mais étant un fan de math je pense connaitre un résultat mathématique surprenant.
C'est samuel monnier qui a découvert un exemple ou en faisant simultanément plusieurs paris qui individuellement sont favorables on se retrouve dans un situation de paris cumulés défavorables.
Cela s'apelle le paradoxe de monnier pour ceux que ca intéresse.

milton > à mon avis il y avait des hypothèses supplémentaires sinon ça ne fonctionne pas (que penses-tu de mon post de 18:27 ?)

Tu as un lien vers ce cours ?

Pour la raison que Kéké a cité, une telle fonction n'a aucune chance d'exister...
Peut-être n'est que continue que lambda-presque partout ? Auquel cas, c'est possible mais c'est également totalement triviale donc j'pense pas que ça soit ça...
J'aimerai bien un lien également vers ledit cours...

Ah quoique... non, c'est pas si triviale que ça mais c'est vrai quand même.

bon
je vous envois le lien.j'ai eu un probleme avec mon pc donc je ne peut pas le commenter avec vous ;mais si vous avez un moyen de l'afficher sans que ce la ne soit en pdf ,je pourai dans ce cas
en voici une autre:
pour tout ensemble donné ,il existe un element de l'ensemble  different de tous les elements de l'ensemble.  

ha j'oubliais; http://www-fourier.ujf-grenoble.fr/~demailly/manuscripts/henstock.pdf

Bonjour,

Sympa cette idee. Ma (pietre) contribution :

pour tout ensemble donné ,il existe un element de l'ensemble  different de tous les elements de l'ensemble >> Euh oui, mais c'est pas un résultat ça... C'est l'axiome de fondation, on décide qu'il est vrai. ^^

kéké >> J'suis sceptique là. C'est quoi que t'appelles dual? L'espace des formes linéaires ou l'espace des formes linéaires continues? Si c'est le deuxième, il manque des hypothèses à ton théorème parce que THE théorème sur les espaces de Hilbert dit qu'ils sont isomorphes (et même isométriques) à leur duaux!

_{En homotopie, ça dépend de ce que tu veux. Je peux bien t'aider comme ne pas du tout comprendre ce dont tu parles...}

Pour moi le dual c'est l'espace des formes linéaires.

_{Pour l'homotopie va faire un tour dans le forum supérieur tu vas comprendre}

Bonjour

Je ne poste pas pour les cadors, mais pour "celui que j'étais avant de me remettre aux maths".

Je croyais que toutes les applications linéaires étaient continues.

Contre-exemple:

E = IR[X] muni de la norme ||P|| = sup|a_k|

et f: P P'

La suite de polynomes Pn(x) = Xⁿ/n  tend vers le polynôme nul, mais la suite des images reste imperturbablement de norme égale à 1.

D'où la non-continuité de f.

Ca m'a beaucoup impressionné à l'époque. Et ça m'a fait toucher du doigt la dimension infinie (ça ne marche pas sur IR_n[X]).

Bonjour jeanseb

Un autre exemple avec et .

est continue relativement à mais pas relativement à .

Par exemple la suite de fonctions suivante :



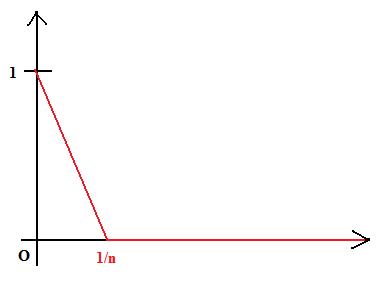
On a et (l'aire du triangle), donc .

Ceci met en défaut la continuité de , car on a une caractérisation bien sympa de la continuité :

continue si et seulement si .

_{En revanche en dimension finie toutes les applications linéaires sont continues.}

Dans un espace de Banach toute série absolument convergente est convergente. Donnons un contre exemple si l'espace vectoriel normé n'est pas complet.

Citation :
Le sous-espace de formé des fonctions à support compact n'est pas complet, et la série des fonctions valant sur est AC mais ne converge pas dans ce sev.