Niveau terminale

les angles orientés

Posté par
moustapha918 12-01-11 à 22:08

bonjours
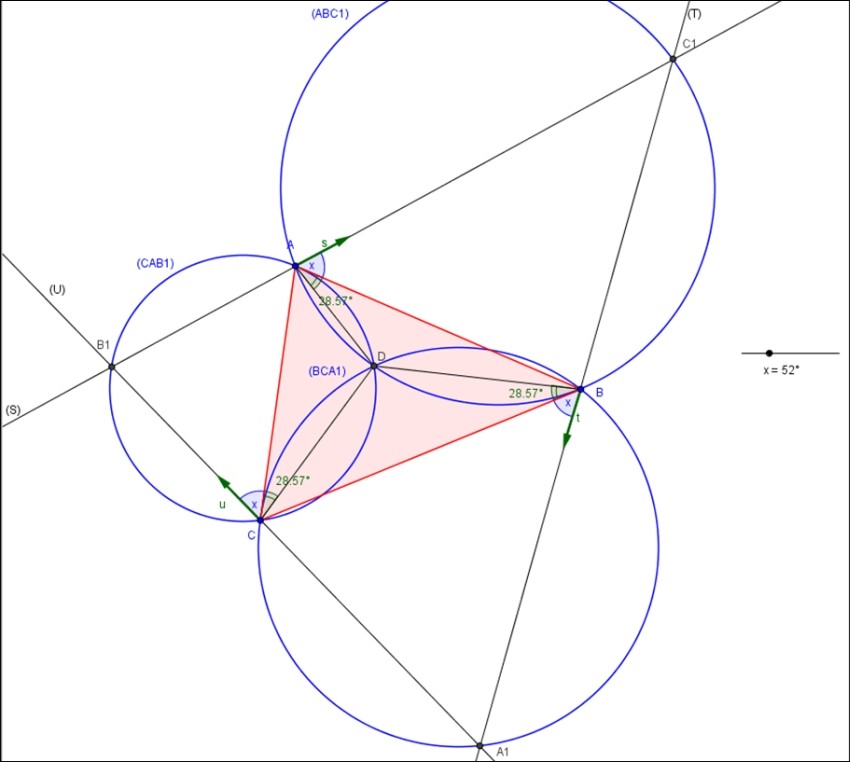
dans le plan orienté on donne un triangle ABC propre et les droites (S),(T) et (U) vecteurs directeurs respectifs s t et u qui passent par A,B et C vérifient (AB;s)=(BC;t)=(CA;u)=x[pu]
on pose A1 =(U) inter (T) B1=(u)inter(S) et C1=(T)inter(S)
1) montrer que (s;u)=(AB.AC) et (t;s)=(BC.BA) .....
2°a)montrer que les cercles circonscrits aux triangles ABC1,BCA etCAB1 ont un point commun D
b)montrer que(AB.AD)=(BC.BD)=(CA.CD)
Je manque la solution de la question 2°b)
et merci

Posté par re : les angles orientés 15-01-11 à 23:00

(réalisé avec Geogebra)

les angles orientés

Posté par re : les angles orientés 15-01-11 à 23:00

Bonjour,

1)

Relation de Chasles :
$3$\left( \vec{s},\vec{u} \right) = \left( \vec{s},\vec{AB} \right) + \left( \vec{AB},\vec{AC} \right) + \left( \vec{AC},\vec{u} \right)$

$3$\left( \vec{s},\vec{u} \right) = -x + \left( \vec{AB},\vec{AC} \right) + x\quad(\pi)$

$3$\left( \vec{s},\vec{u} \right) = \left( \vec{AB},\vec{AC} \right) \quad(\pi)$

2)a) Soit D le point d'intersection des cercles (CAB₁) et (ABC₁).
On veut montrer qu'il appartient également à (BCA₁)

Somme des angles autour d'un point :
$3$\left(\vec{DC},\vec{DB}\right) = 2\pi - \left(\vec{DA},\vec{DC}\right) - \left(\vec{DB},\vec{DA}\right) \quad(2\pi)$

Angles inscrits :
$3$\left(\vec{DC},\vec{DB}\right) = 2\pi - \left(\vec{B_1A},\vec{B_1C} \right) - \left(\vec{C_1B},\vec{C_1A}\right) \quad(\pi)$

Somme des angles dans le triangle A₁B₁C₁ :
$3$\left(\vec{DC},\vec{DB}\right) = \left(\vec{A_1C},\vec{A_1B}\right) \quad(\pi)$

Donc, d'après la réciproque de la propriété des angles inscrits, D est sur le cercle (BCA₁)

2)b)

Une piste de réflexion...

Relation de Chasles :
$3$\left( \vec{AB},\vec{AD} \right) = \left( \vec{AB},\vec{AC_1} \right) + \left( \vec{AC_1},\vec{AD} \right)\quad(2\pi)$

$3$\left( \vec{AB},\vec{AD} \right) = x + \left( \vec{AC_1},\vec{AD} \right)\quad(\pi)$

Angles inscrits :
$3$\left( \vec{AB},\vec{AD} \right) = x + \left( \vec{BC_1},\vec{BD} \right)\quad(\pi)$

$3$\left( \vec{AB},\vec{AD} \right) = x + - \left( \vec{BD},\vec{BA_1} \right)\quad(\pi)$

$3$\left( \vec{AB},\vec{AD} \right) = x - \left( \vec{BD},\vec{BC} \right) - \left( \vec{BC},\vec{BA_1}\right)\quad(\pi)$

$3$\left( \vec{AB},\vec{AD} \right) = x - \left( \vec{BD},\vec{BC} \right) - x\quad(\pi)$

$3$\left( \vec{AB},\vec{AD} \right) = \left( \vec{BC},\vec{BD} \right) \quad(\pi)$

Conjecture sous Geogebra : les trois cercles (CAB₁), (ABC₁) et (BCA₁) ne dépendent pas de x.

Sauf erreur !

Nicolas

Posté par re : les angles orientés 20-01-11 à 15:33

mr nicolas_75 je vous remercie beau-coup de votre aide

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

Autres ressources en terminale
4 fiches de mathématiques sur "Autres ressources" en terminale disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

les angles orientés

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths