- Un petit rappel de Cours sur le dénombrement - terminale
- Sept Exercices Q.C.M. sur le dénombrement - terminale
- Complexes, calcul vectoriel, problème - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
- Enseignement scientifique : suite, probabilité, fonction - sujet de bac - terminale
Inscription / Connexion Nouveau Sujet
les courbes paramétrées
Salut j'ai quelques problèmes à demontrer ça ..
Soit (O,i,j) un repère orthonormé.
Un point A sur l'axe des abscisses et un point B sur l'axe des ordonnées sont tels que AB=1
On se propose de déterminer le lieu géométrique (C) du point M lorsque A et B se déplacent, chacun sur son axe.
1) On note (x,y) les coordonnées de M et t une mesure de l'angle (AB, -i) .
Montrer que (C) est l'ensemble des points M(t) de coordonnées
x = f(t) = sin²t.cost
y= g(t) = cos²t.sint
t appartenant à R
je crois avoir compris où sont les points A et B mais où se trouve le point M ?
es-tu sûr(e) d'avoir copié l'énoncé tel qu'il est écrit ?
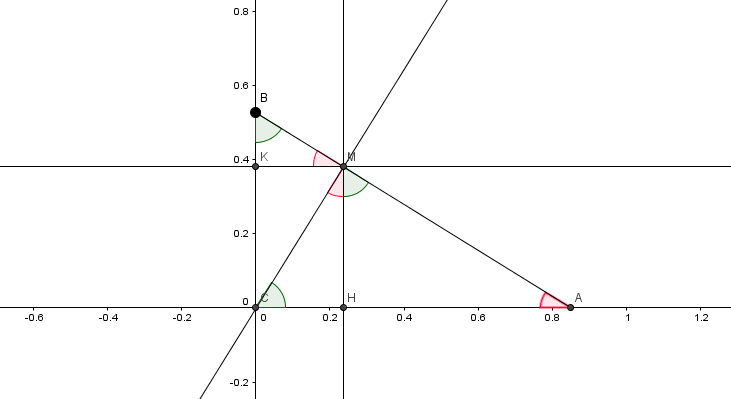
je ne trouve pas tout à fait pareil... ça dépend de "qui est qui" !... mais je pense qu'avec le graphique joint, en comprenant que les angles roses et verts sont complémentaires (somme= /2) et en positionnant l'angle t, tu vas pouvoir commencer
/2) et en positionnant l'angle t, tu vas pouvoir commencer
Bonjour,
Mais si, il faut trouver ce qui est dans l'énoncé.
Si a est l'abscisse de A Et b l'ordnnée de B : a2 + b2 = AB2 = 1
re-correctif : Il faut intervertir dans l'énoncé les coordonnées du point M(t)
l'angle t (non orienté) étant l'angle CBA = angle AOM bleu du schéma de aitomaths qui a raison.
Bonjour,
a et b .... mouais,
m'enfin ils s'éliminent instantanément au profit de t :
abscisse de A = direct en fonction de t
ordonnée de B = direct en fonction de t

non, non
c'est bien ce qui est dit dans l'énoncé sans aucune modification.
t est défini comme l'angle
c'est à dire l'angle rouge de aitomaths
et ça donne bien la formule de l'énoncé, sauf erreur de calcul.
En fait, comme (C), telle que définie dans l'énoncé,
est symétrique par rapport à la première bissectrice y=x,
il n'y a pas à s'inquiéter d'une interversion des coordonnées de M
car l'énoncé ne fait que demander :
Montrer que (C) est l'ensemble des points M(t) de coordonnées
x = f(t) = sin²t.cost
y= g(t) = cos²t.sint
sur ma figure Geogebra le point M est bien celui de coordonnées = les formules de l'énoncé, avec t comme défini sur ma figure
inutile d'inventer autre chose que l'énoncé...
Bonjour mathafou, toujours aussi juste et précis.
et avec la bonne lecture de l'angle (AB, -i) de l'énoncé en



