Niveau Master Maths

Lieu géométrique L d'un point

Posté par
Lyy 31-08-23 à 18:51

Soient $A$ et $B$ deux points distincts du plan et $d$ la médiatrice du segment [AB]. Soient $M$ un point de $d$ , $d_1$ la médiatrice de $[BM]$ et $d_2$ la droite passant par $M$ parallèle à la droite $(AB)$ . Notons $L$ le point d'intersection des droites $d_1$ et $d_2$ .

Chercher le lieu $\mathbb{L}$ décrit par le point $L$ quand $M$ parcourt la droite $d$ .

Moi j'aurais dit: $\mathbb{L}=\{ L \mid M \in (d) \} =\{ L \mid MA=MB \}$

et on sait de plus sur le point $L$ que : $LM=LB$ et $\vec{LM} = k \vec{BA}$ pour un certain réel k.

Ainsi moi j'aurais chercher les coordonées de $M$ .
Soit $M(x_M,y_M), A(x_A,y_A), B(x_B,y_B) et L(x_L,y_L)$ .
Donc comme $\vec{LM} = k \vec{BA}$ on a que $x_M= k(x_A-x_B) +x_L$ et $y_M= k(y_A-y_B) +y_L$

et donc comme M appartient à la droite (d) j'aurais remplacer les coordonées de M dans la condition MA=MB, mais je ne sais pas si mon chemin est juste et je n'obtient pas vraiment une parabole horizontale.. est-ce que quelqu'un pourrait m'aider? (J'ai souvent de problème de chercher les lieu géométriques de tel sorte)

Voici un exemple de dessin:

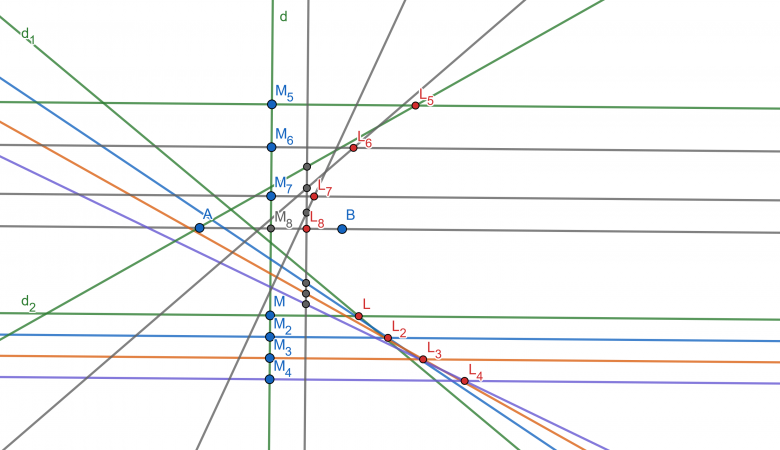
$Lieu géométrique L d\'un point$

Posté par re : Lieu géométrique L d'un point 31-08-23 à 19:52

Bonjour,
$LM=LB$
C'est la définition de la parabole de foyer $B$ et de directrice $d$ .

Posté par re : Lieu géométrique L d'un point 01-09-23 à 11:46

Analytiquement, on peut choisir comme axes du repère la droite $(AB)$ et la droite $d$ sécantes en $O$ milieu de $[AB]$ (et origine de ce repère).

$M(0,y)$ , $L(x,y)$ et $B(a,0)$

$LM=LB\Longleftrightarrow x^2=(x-a)^2+y^2$

et la suite ...

Posté par re : Lieu géométrique L d'un point 04-09-23 à 13:24

lake @ 01-09-2023 à 11:46

Analytiquement, on peut choisir comme axes du repère la droite $(AB)$ et la droite $d$ sécantes en $O$ milieu de $[AB]$ (et origine de ce repère).

$M(0,y)$ , $L(x,y)$ et $B(a,0)$

$LM=LB\Longleftrightarrow x^2=(x-a)^2+y^2$

et la suite ...

Merci! J'ai compris