Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Partager :

Limite et suite

Posté par
Eurotruck 01-04-10 à 20:12

Bonjour,

Soit la suite (un) définie, pour tout entier naturel n tel que n2, par
un= 3$\rm \frac{ln(n!)}{ln(n^n)}.
Etudier la limite de la suite (un).

Vous pouvez ne pas blanquer

Posté par
music_sabre : Limite et suite 01-04-10 à 21:32

Salut,

Je suis pas trop forte en calcule de limite, mais je peux essayer de t'aider...

Tu sais que n^n, est toujours plus grand que n!
et que l'écart entre les deux est toujours plus grand (pour n=2 l'écart 2, pour n=3 écart 21,... )

Et ln est une fonction strictement croissante, donc ln(n!)<ln(n^n)

Et si n tant vers l'infini, ta suite va tendre vers 0

ça me semble logique,...

Mais maintenant, je n'ai pas encore vu ça...

Est-ce que ça t'aide ?

Posté par
athrunre : Limite et suite 01-04-10 à 21:43

Ce n'est pas aussi facile que ça étant donnée la faible croissance de la fonction logarithme népérien.

Posté par
music_sabre : Limite et suite 01-04-10 à 22:04

Ouais, mais si l'écart entre n! et n^n est toujours plus grand si n tant vers l'infini. l'écart lui aussi tend vers l'infini

Donc n^n est infiniment plus grand que n!

Posté par
athrunre : Limite et suite 01-04-10 à 22:14

Ce que tu dis est vrai. En revanche, plus n est grand, moins nln(n) croît.
L'écart entre les abscisses devient de plus en plus grand mais  simultanément l'écart entre les ordonnées relatives de ces abcisses devient de plus en plus petit.

Posté par
music_sabre : Limite et suite 01-04-10 à 22:24

Bon j'ai demandé à mon ordi de le calculer et effectivement, ça ne donne pas zéro, mais 1

Voilà, la limit vaut 1...

Maintenant comment la calculer...

Posté par
MatheuxMatoure : Limite et suite 01-04-10 à 22:46

bonsoir

sauf erreur de ma part...

4$ u_n = \frac{1}{ln(n)} . \[ \frac{1}{n} \sum_{k=1}^{k=n} ln\(\frac{k}{n}\) \] + 1

et la quantité entre crochet converge vers 2$\int_0^1 ln(t).dt qui vaut (-1)

et donc le tout tend vers 1

MM

Posté par
verdurinre : Limite et suite 01-04-10 à 23:58

Bonsoir.
On peut aussi utiliser la formule de Stirling :    
3$ n !\sim \sqrt{2\pi n}\,\left({n \over \text{e}}\right)^n  
qui entraine de façon évidente que la limite de u_n est 1

Posté par
MatheuxMatoure : Limite et suite 02-04-10 à 00:01

(bonsoir Verdurin)
oui, tu as raison, mais j'ai essayé d'éviter de sortir l'artillerie lourde !

Posté par
verdurinre : Limite et suite 02-04-10 à 01:04

Bonsoir MatheuxMatou
Tu donnes une démonstration ce que je ne fais pas. Je la trouve d'ailleurs élégante, quoiqu'elliptique.
J'aurais fait beaucoup plus lourd

En fait si je donne la formule de Stirling, c'est que je trouve que son existence est intéressante pour la culture mathématique des posteurs précédents.

Posté par
athrunre : Limite et suite 02-04-10 à 19:53

Merci MatheuxMatou et verdurin

J'avais à l'idée que cette suite convergeait mais alors vers 1


mais vos démonstrations restent difficilement compréhensibles pour un néophyte comme moi ...


MatheuxMatou :

3$n\in\mathbb{N}\backslash\{0;1\} :

5$\frac{\ln(n!)}{\ln(n^n)}=\frac{1}{\ln(n)}\times\[\frac{1}{n}\ln(n!)\]=\frac{1}{\ln(n)}\times\[\frac{1}{n}\sum_{k=1}^n\ln(k)\]

5$\frac{\ln(n!)}{\ln(n^n)}=\frac{1}{\ln(n)}\[\frac{1}{n}\[\(\sum_{k=1}^n\ln(\frac{k}{n})\)+n\ln(n)\]\]

5$\frac{\ln(n!)}{\ln(n^n)}=\frac{1}{\ln(n)}\[\frac{1}{n}\sum_{k=1}^n\ln(\frac{k}{n})\]+\frac{1}{\ln(n)}\times\frac{1}{n}\times n\ln(n)= 6$\blue\fbox{\frac{1}{\ln(n)}\[\frac{1}{n}\Bigsum_{k=1}^n\ln(\frac{k}{n})\]+1}


Voilà je pense déjà avoir réussi à transformer 3$u_n, mais bon faut l'idée aussi ...

maintenant dire que le "truc" entre crochet converge vers 4$\Bigint_0^1\ln(t)dt ... je n'arrive plus à suivre



verdurin :


Avec une petite recherche (merci Wiki :p)

j'ai donc vu que 4$n!\sim\sqrt{2\pi n}{(\frac{n}{e})}^n était une manière d'écrire :

4$\lim_{n\rightarrow+\infty}\[\frac{n!}{\sqrt{2\pi n}{(\frac{n}{e})}^n}\]=1

donc si j'ai bien compris, lorsque 4$n tend vers 4$+\infty,     4$n!      et     4$\sqrt{2\pi n}{(\frac{n}{e})}^n ont même limite.


Là je ne suis pas sûr de ce que j'écris mais ça me semble être ça :

5$\lim_{n\rightarrow+\infty}\[\frac{\ln(n!)}{\ln(n^n)}\]=\lim_{n\rightarrow+\infty}\[\frac{\ln(\sqrt{2\pi n}(\frac{n}{e})^n)}{\ln(n^n)}\]=\lim_{n\rightarrow+\infty}\[\frac{\ln(\sqrt{2\pi n})+n\ln(\frac{n}{e})}{n\ln(n)}\]=\lim_{n\rightarrow+\infty}\[\(\frac{\ln(2\pi)}{2n\ln(n)}+\frac{1}{2n}-\frac{1}{\ln(n)}\)+1\]

La quantité dans la grande parenthèse tend vers 0 donc 6$\blue\fbox{\lim_{n\rightarrow+\infty}\[\frac{\ln(n!)}{\ln(n^n)}\]=1}

Posté par
ladiiiere : Limite et suite 02-04-10 à 20:06

Moi je ne comprend pas comment on dit que ln (n!) = somme de 1 à n (avec k) de ln(k) :O c'est pas plutôt produit ? Ou alors je n'ai pas suivi ^^

Posté par
ladiiiere : Limite et suite 02-04-10 à 20:12

car pour moi, 4$n! = \prod_{k=1}^{n} k donc 4$ln(n!) = ln(\prod_{k=1}^{n} k) et vous marquez que 4$ln(n!)=ln(\sum_{k=1}^{n})  Je ne comprend plus ^^

Posté par
ladiiiere : Limite et suite 02-04-10 à 20:13

Non enfait j'ai mal lu ^^ excusez moi

Posté par
athrunre : Limite et suite 02-04-10 à 20:34

Bonsoir ladiiie,

5$\red\fbox{\ln(n!)=\ln\(\Bigprod_{k=1}^nk\)=\Bigsum_{k=1}^n\ln(k)}

Posté par
athrunre : Limite et suite 02-04-10 à 20:35

il est vrai que c'est un peu le foutoir ^^

Posté par
ladiiiere : Limite et suite 02-04-10 à 21:04

D'accord ^^ et ça ça sort de ... ? On le démontre comment ? XD

Posté par
music_sabre : Limite et suite 02-04-10 à 21:20

ladiiie

C'est une propriété des logarithmes : log(a) + log(b) = log(ab)

La preuve se fait par l'élasticité sur l'intégrale de la fonction de 1/x

Posté par
athrunre : Limite et suite 02-04-10 à 21:44

... avec a et b réels strictements positifs.

Posté par
ladiiiere : Limite et suite 02-04-10 à 21:46

D'accord merci bien du renseignement ^^

Posté par
carpediemre : Limite et suite 03-04-10 à 11:04

salut

l'astuce de MatheuxMatou est tout simplement d'ajouter ... 0 !!!!

ln(n!)=ln(n!)-ln(nn)+ln(nn) puis de regrouper les 2 1e termes en une somme correspondant à une intégrale de Riemann à l'aide de la formule ln(a)-ln(b)=ln(a/b) et enfin de diviser par ln(nn)....

Posté par
Eurotruckre : Limite et suite 03-04-10 à 11:14

Merci de vos réponses La solution de l'énigme est 1

Posté par
athrunre : Limite et suite 03-04-10 à 18:29

Ah intégrale de Riemann connaît pas

Posté par
olive_68re : Limite et suite 05-04-10 à 02:23

Salut à tous

On peut faire encore niveau terminal :

Citation :
Si 3$x\in [k,k+1] :

         3$\ell n(k) \, \le \, \ell n(x) \, \le \, \ell n(k+1)

On intègre la bête entre 3$[k,k+1] :

         3$((k+1)-k)\ell n(k)\, \le \, \Bigint_k^{k+1} \, \ell n(x)\, \tex{d}x \, \le \, ((k+1)-k)\ell n(k)  soit  3$\ell n(k)\, \le \, \Bigint_k^{k+1} \, \ell n(x) \, \text{d}x \, \le \, \ell n(k+1)

On somme le tout de 3$1 à 3$n :

         3$\Bigsum_{k=1}^n \ell n(k) \, \le \, \Bigint_1^{n+1} \ell n(x) \, \text{d}x   ( Le reste de l'inégalité on en a pas besoin )

Au final, 3$\ell n(n!)\, \le \, \Bigint_1^{n+1}\ell n(x) \, \text{d}x.


En faisant le même travail en prenant 3$x dans 3$[k-1,k] on obtient l'encadrement :

              3$\fbox{\Bigint_1^n \, \ell n(x) \, \text{d}x\, \le \, \ell n(n!)\, \le \, \Bigint_1^{n+1}\ell n(x) \, \text{d}x

De plus, une primitive de 3$\ell n(x) est 3$x(\ell n(x)-1).

Donc 3$\red \fbox{n\ell n(n)-n+1\, \le \, \ell n(n!)\, \le \, (n+1)\ell n(n+1)-n


On peut donc encadrer notre suite,  3$\fr{n\ell n(n)-n+1}{\ell n(n^n)} \, \le \, u_n \,\le \, \fr{n\ell n(n+1)+\ell n(n+1)-n}{\ell n(n^n)}

Pour 3$n\ge 2 :    3$\blue \fbox{1-\fr{1}{\ell n(n)}+\fr{1}{n\ell n(n)}\, \le \, u_n \, \le \, \fr{\ell n(n+1)}{\ell n(n)}+\fr{1}{n}\times \fr{\ell n(n+1)}{\ell n(n)}-\fr{1}{n}

Comme 3$\fr{\ell n(n+1)}{\ell n(n)} \, \, \longright_{n\to +\infty} \, \, 1, on en déduit par passage à la limite et en utilisant le th. des gendarmes que 3$\red \fbox{u_n\, \, \longright_{n\to +\infty} \, \, 1


athrun >> (comme j'ai l'impression que ça t'interresse je me suis permis d'écrire un petit truc)
Citation :
Bon je ne suis pas sur que l'interprétation que je vais en faire soit exacte en tout point ( j'ai pas encore vu ça en cours ) mais si on trace 3$f:\, x\to \ell n(x), on peut essayer de voir ce que ça donne graphiquement : ( Pour l'instant ne t'occupe pas de ce qui est en vert et bleu )

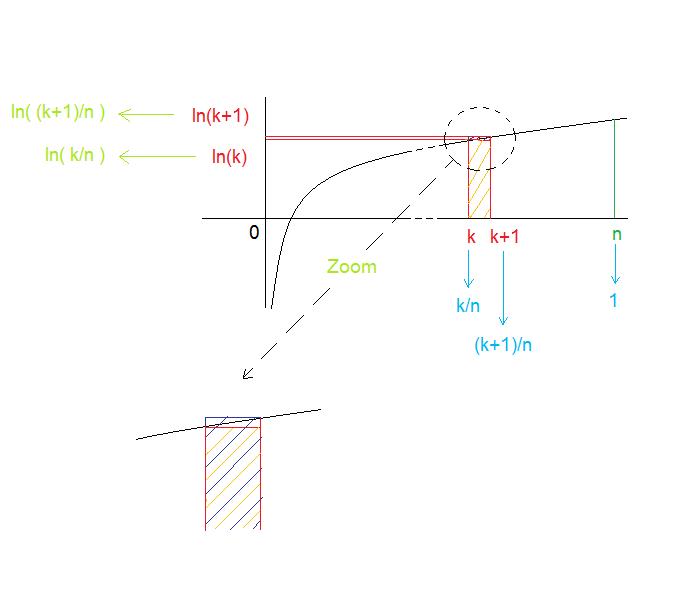
              Limite et suite

On voit bien que l'on a l'encadrement " 3$\rm Somme de l'aire des rectangles sous la courbe \le \Bigint_1^n \ell n(x) \text{d}x \le Somme de l'aire des rectangles au dessus de la courbe " 3$(*).

Le problème c'est que par passage à la limite, il manque une infinité de petit bout sous la courbe qui rend le calcul d'aire très imprécis (voir le zoom, le rectangle du haut est l'erreur commise) , alors on aimerait bien que plus 3$n grandit, plus la largeur des rectangles devient petite, car les rectangles recouvreront d'autant plus tout l'aire sous la courbe.

Mais problème : plus 3$n grandit, plus l'intervalle qu'on considère grandit.


Tout comme avant, tu as une somme ( 3$\frac{1}{n}\Bigsum_{k=1}^n\ln(\frac{k}{n}) ) d'aire de rectangle, cette fois de largeur 3$\fr{1}{n} et de hauteur 3$\ell n\(\fr{k}{n}\).

On peut donc se ramener au même dessin que avant ( changements en vert et bleu ).

On encadre de la même manière la fonction avec des rectangles sous la courbe dont le k-ieme est d'aire 3$\cal{A}_k et des rectangles sur la courbe dont le k-ieme est d'aire 3$\cal{A}^k.

Ce qui change ( et tant mieux en fait ) c'est que plus 3$n grandit, plus la largeur du rectangle devient petite ( je te renvoie quelques lignes plus haut ).

( En fait, ca se voit graphiquement 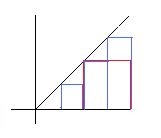 Limite et suite ( j'ai pris une autre courbe pour caricaturer la différence ) )

L'erreur commise sur l'encadrement du k-ieme rectangle est 3$\varepsilon_k=\cal{A}^k-\cal{A}_k mais comme notre subdivision de l'intervalle ( ça s'appelle comme ça, ici : 3$0<\fr{1}{n}<\fr{2}{n}<...<\fr{n-1}{n}<1 ) est de plus en plus fine alors 3$\varepsilon_k \, \longright_{+\infty} \, 0 au point que 3$\varepsilon \, \longright_{+\infty} \, 0.

Quand on fait tendre 3$n vers l'infini on a donc 3$\Bigsum_{n\ge 1} \, \cal{A}_k \, = \, \Bigsum_{n\ge 1} \, \cal{A}^k\ .

D'après Th. des gendarmes cette limite existe (existe car l'aire des rectangles est fini) et d'après 3$(*) vaut 3$\Bigint_0^1 \, \ell n(x)\, \text{d}x.

D'où le résultat de Alain.

(C'est valable entre autre pour les fonctions continues, pour une telle fonction : 3$ \fr{b-a}{n}f\(a+k\fr{b-a}{n}\) \, \, \longright_{+\infty} \, \, \Bigint_a^b \, f(x) \, \text{d}x ).


Voilà, j'espère que c'est un minimun clair

Posté par
olive_68re : Limite et suite 05-04-10 à 02:44

(Ah oui j'ai oublié, pour l'exercice j'ai pas de mérite, j'avais déjà fait l'exercice l'année dernière dont je me souvenais de la méthode)

Posté par
olive_68re : Limite et suite 05-04-10 à 02:50

Encore un oublie : athrun >> quand je dis "on encadre la fonction" on a l'impression qu'elle apparaît par magie, mais en fait la somme à une tête assez sympa pour qu'on puisse l'écrire comme je l'ai mis dans la dernière ligne de mon post avec 3$f à déterminer, ici on voit que le 3$\ell n convient.

Posté par
athrunre : Limite et suite 05-04-10 à 21:58

Merci pour tout Olive

c'est en effet très intéressant !


tu as aussi un très joli \LaTeX ^^

Posté par
olive_68re : Limite et suite 12-04-10 à 16:24

Je t'en prie

Merci

Posté par
gui_toure : Limite et suite 13-04-10 à 13:21

Bonjour à tous,

Je constate que tu as fait d'énormes progrès Olive, aussi bien en maths qu'en LaTeX Continue comme ça !

Posté par
olive_68re : Limite et suite 14-04-10 à 20:07

Salut gui_tou

Merci pour ces encouragements, pourtant l'impression de stagner ..

Bon courage pour tes concours, en espérant que ce soit plus payant que l'année dernière ( on te fait confiance pour ça ) !


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !