Niveau algorithmique

logique combinatoire

Posté par
galaxye 16-01-13 à 13:11

Bonjour à tous,

Je viens de débuter dans le monde de l'électronique et deja que je bute dans une "devinette" j'aurais besoin de votre aide

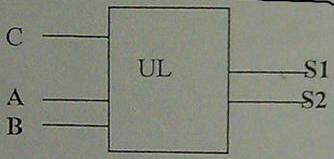
C'est l'étude d'une unité logique UL à 2 entrées principales A et B, une entrée de sélection C et à 2 sorties S1,S2

Schéma en pièces jointes.

Si on commande l'entrée C=1 la sortie S1 est le resultat d'une fonction ET avec les deuc entrées A et B mais la sortie S2 est le résultat d'une fonction OU
Si on n'active pas l'entrée C la sortie S1 devient une fonction NAND et la sortie S2 une fonction OU exclusif.

Le but étant de rechercher en les simplifiant les équations de commande des sorties S1 et S2.
et faire le schéma correspondant de l'unité logique (Avec des ET,OU,NAND,OU exclusif à 2 et 4 entrées)

La deuxieme partie me semble simple mais alors je sèche (ou je ne comprends pas le sens ?) de la premiere partie ?

C'est un exercice type que j'aimerais retravailler pour ce week end.

Merci de votre aide.

logique combinatoire

Posté par re : logique combinatoire 16-01-13 à 13:36

Bonjour,

Pour la première partie, il faut écrire les équations logiques (avec . = ET, = OU):
S1 = C.(A.B) $\bar{C}$ .( $\bar{A.B}$ )
S2 = C.(AB) $\bar{C}$ .( $A.\bar{B}$ $\bar{A}.B$ )
Les expressions de S1 et S2 peuvent ensuite être simplifiées un peu pour l'élaboration du schéma (j'ai laissé des parenthèses inutiles pour la compréhension et bien entendu ces résultats sont à revérifier !).

Cordialement.

Posté par re : logique combinatoire 17-01-13 à 07:24

Merci beaucoup, je commence à capter la chose

Par contre pourrais t'on simplifier les équations ?Et comment arriver à ce résultat ?

Posté par re : logique combinatoire 17-01-13 à 10:29

Pour simplifier ces équations, on peut utiliser les lois de De Morgan (ici ). Par exemple:
S1 = C.(A.B) $\bar{C}$ .( $\bar{A.B}$ )
= A.B.C $\bar{C}$ .( $\bar{A}$ $\bar{B}$ )
= A.B.C $\bar{A}$ . $\bar{C}$ $\bar{B}$ . $\bar{C}$
Il s'agit ici à vrai dire plus d'un développement que d'une simplification mais il permet de construire plus facilement le schéma logique. Il y a aussi les tables de Karnaugh qui constituent une approche systématique pour la simplification (ici ).

Posté par re : logique combinatoire 17-01-13 à 18:25

Merci homeya J'ai finie l'exo et je vais retravailler dessus.

J'ai besoin encore une fois de votre aide.
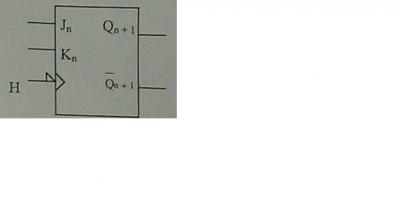
Donner la table de vérité et la table de transition correspondant au fonctionnement de la bascule suivante:

Avec ce type de bascule, on veut réaliser un compteur réfléchi (Code Gray)sur 3 bits.
Au départ les états de sorties Q2Q1Q0=000
questions:
quel est le tableau d'analyse de ce compteur ?
En déduire les équations de commande des bascules.
Présenter le schéma de principe du compteur.

Merci encore

logique combinatoire

Posté par re : logique combinatoire 18-01-13 à 10:33

Les tables de vérité et de transition des bascules JK peuvent être trouvées ici . Concernant le compteur Gray, le tableau d'analyse et les équations de commande d'un compteur 4 bits peuvent être trouvés ici (la page est également intéressante).