Inscription / Connexion Nouveau Sujet
Moins d'un rectangle dans un carré
Bonjour à tous 
Dans le carré ci-dessous on a disposé cinq rectangles identiques .
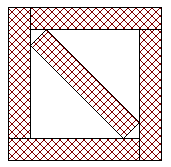
Est-il possible de placer un certain nombre de ces rectangles dans ce même carré de façon à ce que l'aire de la partie laissée libre soit strictement inférieure à celle d'un rectangle ?
Imod
PS : Je souhaite une méthode plus qu'une réponse non justifiée .
Bonjour,
la première chose à faire à mon avis est de calculer les dimensions du rectangle de sorte que les 5 placés ainsi collent
en prenant le côté du grand carré comme unité par exemple.
...
 Cliquez pour afficher
Cliquez pour afficherOn progresse à grand pas 
Certains auront peut-être remarqué qu'il y a une identité remarquable cachée dans le dessin .
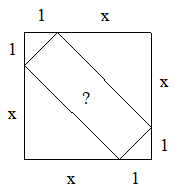
Imod
Les dimensions du rectangle et du carré sont donc et
. Quel argument très simple permet d'affirmer qu'on ne peut pas placer 8 rectangles dans le carré ?
Imod
Bonjour
Prenons l'exemple d'un grand carré de coté 1 et de rectangles de largeur 0.1 et donc de longueur 1-0.1=0.9
Le petit carré à un coté de 1-(0.1+0.1)=0.8
On voit bien qu'aucun rectangle ne se logera parallèlement.
Ici nous pourrons en placer deux inclinés de 0.488 radians
(diagonale de contact 0.9055)
On constate que l'épaisseur (largeur ) maximale pour un tel cas est 0.166 (impossible de loger un seul rectangle
par contre pour des valeurs inférieures on peut loger plusieurs rectangles avec des angle de plus en plus faibles.
il ne s'agit pas de remplir le carré intérieur,
mais de remplir le grand carré avec des rectangles de la taille et forme imposée par la figure initiale mais disposés (éventuellement tous) autrement.
si on ne tient pas compte de la figure initiale, mais qu'on peut choisir la largeur, on pourrait avoir ça en choisissant la largeur des rectangles = 0.25 par exemple
le "reste" hachuré est bien entendu < l'aire d'un carré (strictement)
Mais on impose la valeur unique et exactement définie par la figure de l'énoncé : rectangle intérieur incliné à exactement 45°
on ne peut pas faire varier (choisir) les dimensions.
on ne peut que faire varier la disposition des rectangles dans le grand carré.
comme "par exemple" :
 Cliquez pour afficher
Cliquez pour affichermoi je comprends le problème ainsi.
pas en laissant libre le rectangle intérieur
Suite
Avec un carré ,je me doutais bien qu'il y avait du 2..
2..
mon angle passe à 45 ° et la limite de largeur pour les rectangles de la figure à 0.147 .
Pour clore le problème :
Sylvieg et Mathafou on montré comment on pouvait placer 7 rectangles dans le carré . Il reste alors dans le carré une aire équivalente à celle d'un rectangle , or on veut moins , on doit donc ajouter un rectangle qui recouvrira alors complètement le carré . Les 8 rectangles seraient alors disposés parallèlement aux côtés du carré . Or sur un côté du carré on ne peut pas mettre 7 longueurs ni 6 longueurs plus deux largeurs , on est donc coincé .
Imod



