Inscription / Connexion Nouveau Sujet
Non ! pas la règle encore !!
Bonjour,
comme vous aimez visiblement ça, je persiste...
On donne un cercle de centre O
inscrire un polygone régulier à la règle seule (la fameuse règle, celle de longueur infinie et à un seul bord sans graduations ni possibilité d'y inscrire des marques)
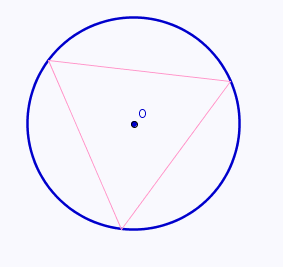
déja un carré et un triangle équilatéral ...
l'hexagone suit dans la foulée du triangle équilatéral.
le reste est plus dur et je ne le demande pas !!
Pour la petite histoire, un certain Karl von Staudt a réalisé en 1842 la construction dans ces conditions du polygone régulier à 17 côtés.
Bonjour
Je ne connais pas les "tenants et aboutissants" des discussions antérieures et j'ai une question concernant cet "exercice" :
"Pourquoi utiliser uniquement une règle et ne pas utiliser également un compas ?"
parce que avec un compas c'est trop facile ...
les constructions géométriques se font avec des outils "imposés"
on choisit les règles (du jeu  ) et il faut faire "avec ces règles"
) et il faut faire "avec ces règles"
- le traditionnel "règle (non graduée) et compas"
mais aussi :
- règle seule, toute seule (bof pas grand chose de constructible)
- règle + quelque chose de donné : ici un cercle,
dans une construction précédente (d'où le titre) un segment donné et une unique parallèle à ce segment
- règle + un autre outil, par exemple règle + équerre seule (sans compas)
- compas seul (sans règle)
etc etc ...
noter que le traditionnel "règle + compas" ne permet pas de construire tout.
les Grecs et depuis, des générations de chercheurs, se sont escrimés sur la quadrature du cercle (construire à la règle et au compas un carré de même périmètre qu'un cercle donné) jusqu'à ce qu'on démontre que c'était impossible.
de même pour la trisection de l'angle : c'est impossible avec seulement la règle et le compas.
de même pour la construction de polygones réguliers en général sauf si le nombre de côtés est de la forme 2nD où D est un produit de nombres premiers "de Fermat" distincts.
on n'en connait que cinq : 3, 5, 17, 257 et 65537
le polygone régulier à 7 côtés n'est ainsi pas constructible à la règle et au compas (de façon exacte, on s'intéresse ici exclusivement à des constructions "mathématiquement exactes") le polygone à 17 côtés oui.
et même celui à 257 côtés et à 65537 côtés, à 51 côtés (= 3*17) etc
mais pas celui à 9 (= 3*3 pas distincts)
on peut ajouter aussi des "outils exotiques" :
- un outil capable de trisecter des angles. avec des systèmes articulés, des engrenages etc ...) on s'en fiche de cette réalisation "mécanique" on est ici dans le dommaine de la géométrie théorique, avec une précision infinie.
- un outil capable de tracer de façon continue des coniques (ellipses, hyperboles, paraboles) etc etc ...
- des courbes auxiliaires "toute tracées"
bref on fixe les règles du jeu : tel outil, telles restrictions
et on cherche à résoudre le problème posé en n'utilisant que ces outils là.
ici juste une règle et le cercle déja tracé. (tracé par magie : il est "donné")
une sorte de défi mathématique : je pourrais le faire avec tous les outils (c'est même facile) mais par défi je veux n'utiliser que la règle seule.
Steiner a prouvé que tous les points constructibles avec la règle et le compas sont aussi constructibles avec la règle seule, pourvu qu'on ait un unique cercle et son centre donné.
ici c'est donc possible, et le défi est de le réaliser pratiquement...
Bonjour à tous,
"Pourquoi utiliser uniquement une règle et ne pas utiliser également un compas ?"
Pourquoi gravit-on les montagnes ?
A cette question, George Mallory a répondu:
"Parce qu' elles sont là"

Bonjour,
Quoi qu'il en soit,nous pouvons déja remercier
mathafou pour le travail qu'il produit...
On va chercher...
Question:
Avec cette fameuse règle (que je n'achèterais pour rien
au monde), est-on capable de tracer une tangente au cercle?
Dans la "vraie" vie on y arrive par petits glissements
Oui
cela fait même partie des "classiques" à la règle seule
et pour faire ça on n'a même pas besoin de connaitre le centre du cercle (alors que pour mon "énigme", si, le centre est indispensable)
je donne cette construction hyper classique :
étant donné un cercle et un point P extérieur au cercle, construire à la règle seule les tangentes au cercle passant par P
 Cliquez pour afficher
Cliquez pour afficherParmi les classiques "à la règle seule" + une parallèle (avec le cercle, la première tache va être de "fabriquer" ces parallèles) :
- milieu d'un segment
- parallèle passant par un point P quelconque aux deux parallèles données (ici aux deux parallèles construites)
Bonjour
Si,SI! encore,je vais devenir un spécialiste du
théorème de Poncelet-Steiner
Ton travail étant remarquable,il faut que de nouveaux adeptes
nous rejoignent ainsi,je suis déja en mesure de tracer un carré
inscrit ainsi qu'un octogone
Bien !!
tu peux même généraliser ton octogone à tous les polygones réguliers à 2n côtés comme le hexakaidecagone (beurk)
Bonjour
Dommage que je ne sois pas pratiquant de géogebra
car sur excel les images prennent trop d'octets.
Lorsqu'on connait la méthode des parallèles et des perpendiculaires,c'est vrai que la règle seule permet
de nombreuses figures.
Pour te remercier je te donne un résumé de mon approche
en attendant d'autres progrès:
 Cliquez pour afficher
Cliquez pour afficherBonjour,
"3/je trace une perpendiculaire quelconque à ce diamètre"
ah bon ?? comment ?
les seules perpendiculaires qu'on peut tracer ne sont justement pas quelconques.
ensuite pour tracer une parallèle à cette droite là il faudrait deux perpendiculaires au même diamètre.
Pour être sûr de ne pas faire de construction "fausse", le mieux est de se restreindre exclusivement au seul et unique outil  de Geogebra
de Geogebra
ou idem avec Car (Compass and Ruler) alias ZuL (Zirkel und Lineal) etc autres logiciels de Geométrie :
se restreindre exclusivement à l'outil "droite passant par deux points" et uniquement celui là.
(s'interdire les raccourcis du genre "on sait faire ci ou ça", le faire explicitement par "droite" et rien d'autre)
nota : la construction des tangentes, est ici inutile, mais bon il doit surement y avoir plusieurs constructions possibles, hein, pourquoi pas une avec construction de ces tangentes ...
"car sur excel les images prennent trop d'octets."
copie d'écran et coller dans Paint, découper etc enregistrer en format gif ou png.
Merci pour tes conseils
je pense que tu n'as pas compris mon point 3
1/mont point A est issu de la tangente que j'ai
tracée par ta methode
2/mont point C est le symétrique (diamètre)
3/une perpendiculaire à ce diamètre m'est nécéssaire
pour cela je prend un point Q quelconque hors du cercle
je trace AQ qui coupe le cercle en I
je trace QC qui coupe le cercle en J
suite
je trace AJ
IC et AJ se coupent en Q'
QQ' est perpendiculaire à AC (cqfd)
4/Il ne me reste plus qu'à tracer la parallèle
par le centre (1 point deux parallèles)
Bravo à tous deux.
(je n'avais effectivement pas bien compris ce que faisait dpi)
toutefois la méthode avec des parallèles n'est pas la plus efficace ici : la méthode avec les milieux est un peu plus rapide... par contre ne construit pas un carré inscrit avec un sommet choisi mais "un carré quelconque" inscrit.
 Cliquez pour afficher
Cliquez pour afficherau triangle maintenant ...
Bonsoir,
>>>mathafou
En choisissant un diamètre AB quelconque, on peut construire n'importe quel carré !
Bien à vous
Bonsoir,
La question n'est pas vraiment là.
Bien sûr "on peut", mais je discutais du "simplement".
avec ta méthode, tu choisis le diamètre AB et tu construit non pas n'importe quel carré mais le carré de diagonale AB.
tu est donc "le maitre" direct du choix du carré.
ma méthode est plus simple, mais je ne suis pas le maitre du choix de quel carré sera construit au final.
c'est "la surprise" le carré construit !
le mieux est alors "un hybride" des deux méthodes :
 Cliquez pour afficher
Cliquez pour afficherBonjour,
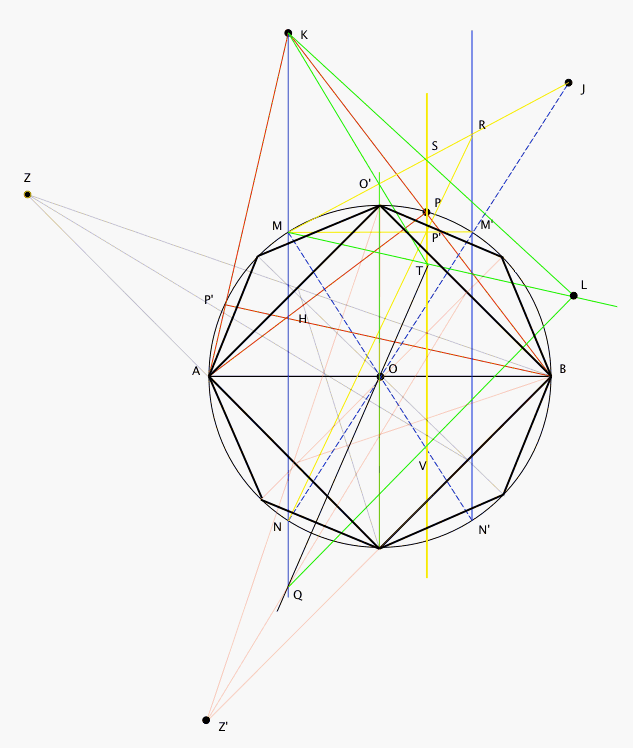
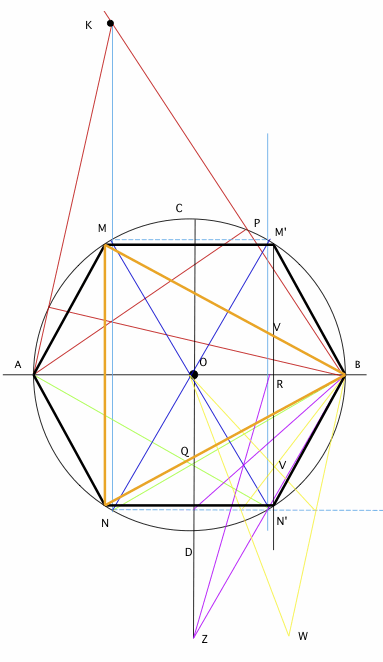
je continue avec la construction à la règle seule du triangle équilatéral et de l'hexagone
 Cliquez pour afficher
Cliquez pour afficherA bientôt, bon décodage !
Bonjour,
C'est presque ça sauf le point V (pourquoi y a-t-il deux points V au fait ?)
tu devrais vraiment te mettre à Geogebra ou autre logiciel de géométrie qui permet de faire varier facilement ton "on choisit W quelconque" ...
(et qui met les points d'intersection pile dessus et pas à côté)
je sens que c'est presque fini cette énigme... je n'ai plus qu'à en préparer une autre.
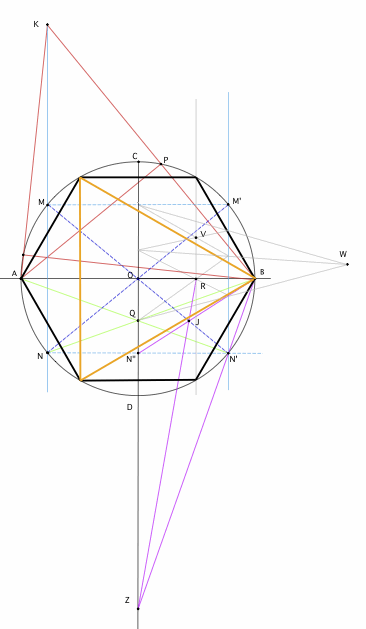
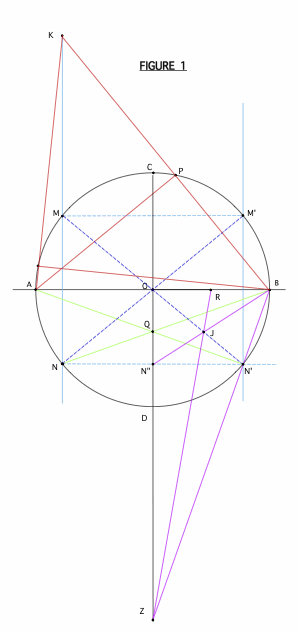
Bonsoir,
>>> mathafou
"Vingt fois sur le métier remettez votre ouvrage,
Polissez-le sans cesse, et le repolissez,
Ajoutez quelquefois, et souvent effacez."
Voilà ce que mon professeur mathafou conseille à son tout petit élève qui lui propose avec respect une construction remaniée de l'hexagone et du triangle équilatéral !
 Cliquez pour afficher
Cliquez pour afficherBonne soirée
Voila Impec 

et hop, terminé.
j'l'avais bien dit qu'il n'y en avait plus pour longtemps sur cette énigme.
Bon Dimanche,
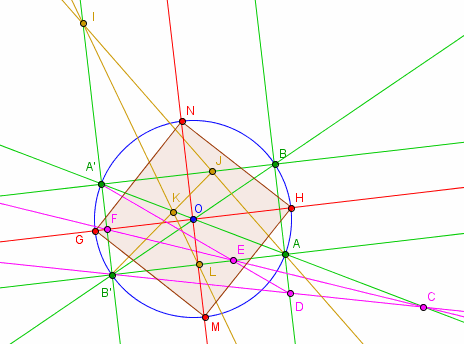
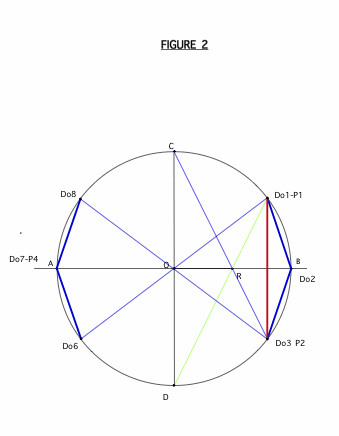
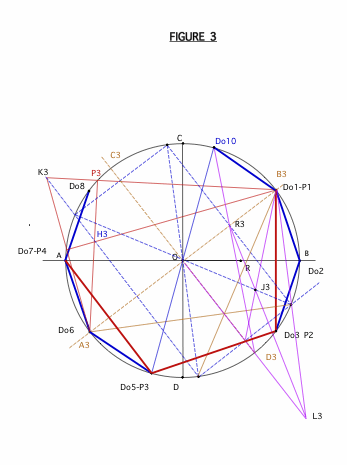
pour l'amusement voici le mode de construction à la règle du décagone et du pentagone.
 Cliquez pour afficher
Cliquez pour afficher(suite au prochain message)
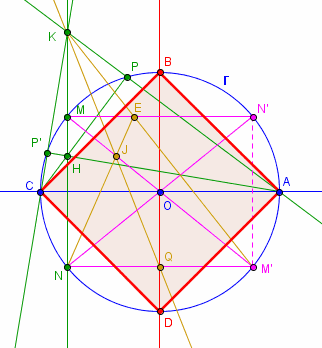
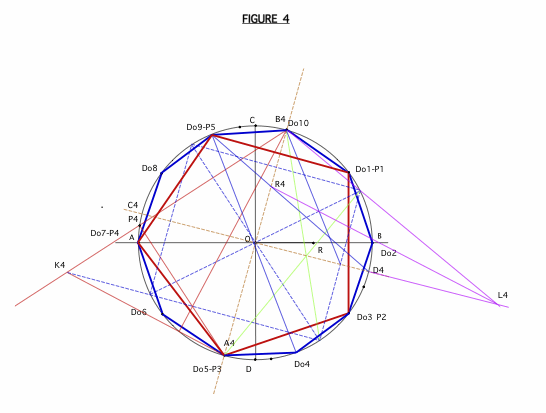
voici la suite ( le site ne permet pas de placer plus de 3 images )
 Cliquez pour afficher
Cliquez pour afficherPour ceux qui sont intéressés, je signale la construction du pentagone par "la Méthode des Compagnons" que j'ai transmise à Madame Léveillau et dont elle a fait une jolie animation sur son site Mathémagic
Bien à vous
Bonjour,
NB. Il y a un petit manque de précision : ..
Laissons tomber provisoirement la règle seule et autorisons nous tous les outils à disposition, y compris Geogebra (soyons modernes).
Tu pars donc de deux diamètres AB et CD et du point R milieu de OB
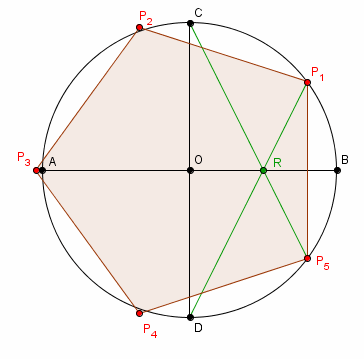
tu prétends que DR (et CR) donnent les sommets P1 et P5 du pentagone.
Geogebra n'est absolument pas d'accord ! (et moi non plus)
un pentagone réellement régulier construit sur ce côté P1P5 ... a ses autres sommets visiblement pas sur le cercle !
cette construction n'est qu'une construction approchée qui a le seul avantage (il est de taille ... de pierre) : sa simplicité.
ici on s'intéresse aux constructions absolument exactes...

Suite...
Je ne demandais pas la construction du pentagone (ni du polygone à 17 côtés  )
)
Castoriginal, tu as fait du zèle 
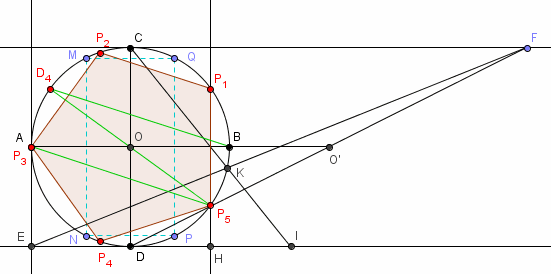
pour les curieux, une construction exacte du pentagone régulier inscrit à la règle seule :
 Cliquez pour afficher
Cliquez pour afficherBonjour dpi,
Il a de moins en moins d'adeptes ce brave Euclide ...
Pour estimer la précision toutefois de la construction "des compagnons"
cette construction donne cos pi/5 = 0.8 tout rond
la vraie valeur étant = 0.809016994...
l'erreur est de moins de 1%
on remarquera que cos pi/5 est la moitié du nombre d'or  =
=
d'où le lien entre le pentagone (et pentagramme) et le nombre d'or / le rectangle d'or.

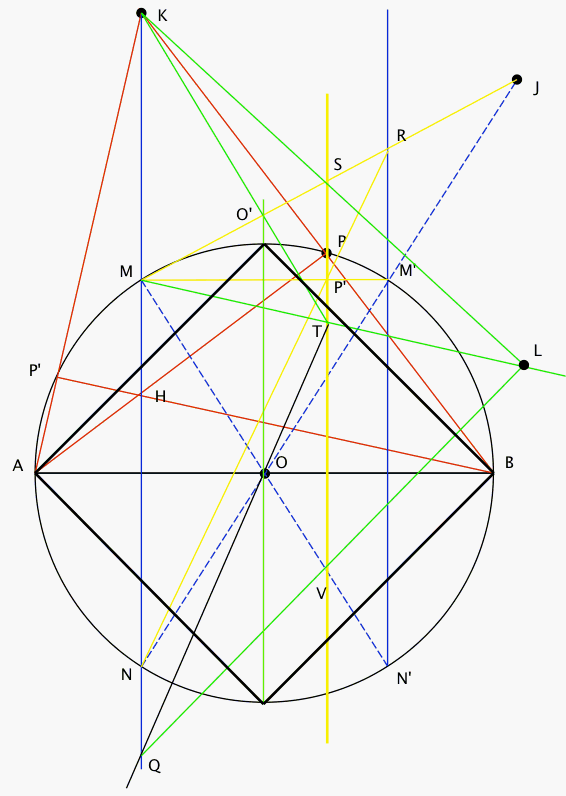
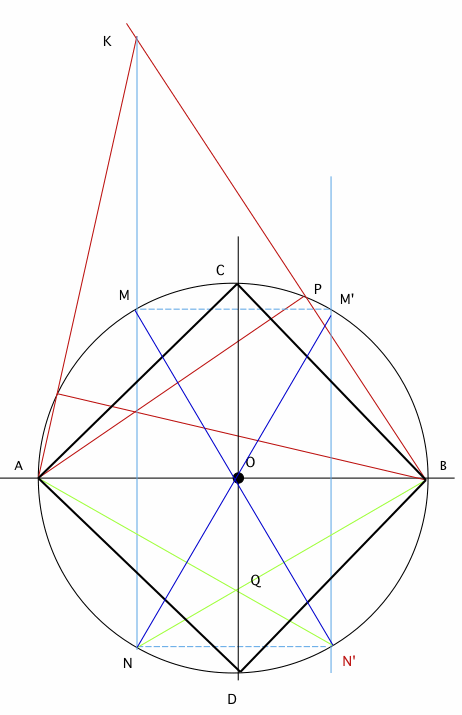
 de centre O et un point A quelconque de ce cercle, soit à construire le carré inscrit de sommet A.
de centre O et un point A quelconque de ce cercle, soit à construire le carré inscrit de sommet A.
 /5) =
/5) = 
