Inscription / Connexion Nouveau Sujet
Normale à une courbe de Bézier
Bonjour.
J'espère être dans la bonne section. À 68 ans, les appellations des sections me restent un peu obscures. En Belgique, ces appellations sont différentes de la France 
Ma question :
Dans un logiciel de dessin, je trace une courbe de Bézier sur laquelle je place différents noeuds.
Je sais trouver les coordonnées de ces noeuds au travers du logiciel (Inkscape) et d'un peu de programmation.
Je voudrais pouvoir tracer les normales à la courbe de Bézier aux emplacements de ces différents noeuds. Ces normales me permettront de trouver les intersections avec une seconde courbe de Bézier qui suit la première et qui lui est plus ou moins parallèle.
Comment puis-je déterminer l'équation de la courbe à un noeud sachant qu'un noeud de Bézier est défini par ses coordonnées x et x (je travaille en 2D) et les coordonnées des "poignées" qui permettent de modifier cette courbe.
Merci.
Bonjour,
apparemment tu as accès aux cordonnées du point et à celle des poignées.
La normale à la courbe est la perpendiculaire à la droite qui passe par le point du nœud et sa poignée.
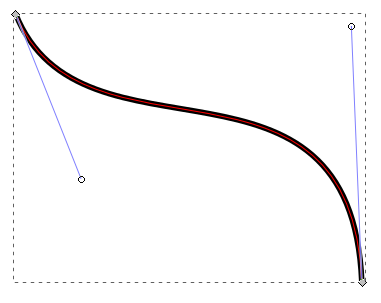
Dans l'image ci-dessus, les perpendiculaires aux droites joignant un carré ( point ) et un rond ( poignée ).
Service. 
J'aimerais te poser une question : comment as-tu accès aux coordonnées dans Inkscape ?
Je me sers de ce programme pour communiquer, mais je fais la base du dessin avec pstricks en LaTeX, ce qui est quand même assez maladroit.
Si tu as une adresse pour une doc de qualité, je t'en serais très reconnaissant.
Bonjour verduren,
Inkscape utilise un système un peu particulier pour permettre de créer des extensions :
1. on crée un fichier .inx qui va contenir les références aux objets contenus dans le dessin et dont on a besoin.
2. On crée ensuite un fichier en python qui va récupérer ces informations fournies par .inx, le manipuler comme on en a besoin. Ce code python a alors la possibilité d'intervenir dans le dessin puisqu'il a reçu les informations nécessaires depuis .inx.
Il faut savoir que Inkscape suit les prescriptions "SVG" et le "recommandations W3C" pour créer les dessins. Le code Python devra aussi suivre ces prescriptions pour pouvoir atteindre les objets contenus dans le dessin.
D'ailleurs, dans Inkscape, il y a l'outil "Xml éditor" qui permet de manipuler les objets du dessin de manière non graphique.
Cette procédure est malheureusement très peu documentée et de nombreux tâtonnements m'ont été nécessaires pour appréhender la chose.
C'est en analysant les extensions de Inkscape (fichiers .inx et.py) qu'il est possible d'appréhender l'approche choisie par les auteurs (par exemple : ![]() ).
).
Le site (http://www.ekips.org/) contient de précieuses informations vraiment très utiles.
Un autre élément indispensable pour pouvoir intervenir dans les fichiers Inkscape est le fichier inkex.py (![]() ).
).
C'est avec toutes ces infos que j'arrive - patiemment  - pas par pas à faire évoluer mon fichier. Je ne suis pas un programmeur professionnel. C'est par nécessité que j'ai tâté de ces outils.
- pas par pas à faire évoluer mon fichier. Je ne suis pas un programmeur professionnel. C'est par nécessité que j'ai tâté de ces outils.
Quelques pages web :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
J'espère que ces infos te seront utiles.
Bonne lecture 
A+



