Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques DétentePour discuter des JFF, des problèmes intéressants. ExercicesExercices ludiques [tout]Lister tous les topics de mathématiques
Niveau exercices
Officiel de la Taupe 167b
Posté par perroquet
(re)Bonjour
Un exercice sur les séries (ENSAM option PSI)
Citation :
Montrer que la suite) définie par
définie par  et
et  tend vers
tend vers 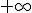 et en donner un équivalent.
et en donner un équivalent.
Montrer que la suite


