Bonjour

comme pour tous les topics : si tu veux des réponses, donne toi la peine de recopier ton énoncé !

Bonjour daxtero

Je te mets ton problème, pas pour moi, les probas, connais pas !

Le dimanche soir, alors que la Belle au bois dormant (appelons-la Aurore) est endormie, nous lançons une pièce de monnaie pour un tirage à pile ou face. Le tirage n'est pas truqué. Si la pièce tombe sur face, le lendemain (le lundi), on réveille Aurore et on a un entretien avec elle. Si c'est pile, on la réveille le lundi, on a un entretien avec elle, puis on la rendort en lui administrant un somnifère à effet amnésique qui lui fait complètement oublier la journée du lundi. Enfin, toujours dans le cas de pile, on la réveille à nouveau le mardi et on a un autre entretien avec elle.

Au cours de l'entretien, on lui pose la question : « Quelle est la probabilité que la pièce soit tombée sur pile ? »

Étant parfaitement au courant des règles, et maitrisant parfaitement les principes de l'inférence bayésienne, que répondra-t-elle ?

À noter qu'à chaque réveil, Aurore ignore si on est lundi ou mardi. Tout ce qui est dans ce paragraphe est bien entendu connu de notre princesse.

Afin que le lecteur comprenne bien le sens de la question posée à Aurore, on peut reformuler ainsi le problème : Si, au cours de l'entretien, Aurore dit « La pièce est tombée sur pile », quelle est la probabilité qu'elle ait raison ?

Louisa

bonjour
je ne comprends pas bien le problème !
le mardi matin, on relance la pièce ?

MM

Bonjour à tous !
Je ne vois pas où est le paradoxe, avec un arbre (s'il elle ne sait pas quel jour on est) :

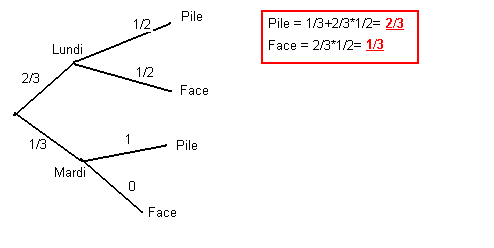
matovitch >>> Ton arbre est faut, car les 3 entretiens possibles ne sont pas équiprobables. De plus, je ne comprend pas ton raisonnement, pourrais tu détailler stp

L'énoncé comporte une ambigüité faut!
Le fait de lui posé la question "Quelle est la probabilité que la pièce soit tombée sur pile?"
ne revient pas à savoir si elle à raison lorsqu'elle dit "La pièce est tombée sur pile." car la question serait alors "Est-ce que la pièce est tombée sur pile?". Ce qui ne revient pas du tout au même.

En effet il y a deux expériences aléatoires différentes :
lancé d'une pièce qui tombe nécessairement sur pile ou face de façon équiprobable
Demander à Aurore "Est-ce que la pièce est tombée sur pile", les 2 issues possibles sont qu'elle à raison où qu'elle à tord.

Par contre, lui demander "Quelle est la probabilité que la pièce soit tombée sur pile?" ne constitue pas une expérience aléatoire...

Si je ne m'abuse, l'énoncé (bien qu'il soit fortement ambigüe ) nous demande d'étudier l'expérience .

Soit R l'évènement : "elle est raison lorsqu'elle dit que la pièce est tombée sur pile"
Si elle affirme que la pièce est tombée sur face alors il faut juste permuter les probabilités et .

Mommons F l'évènement, "la pièce est tombée sur face"
Nommons l'évènement : "on lui pose la question lundi et la pièce est tombée sur face"
Nommons l'évènement : "on lui pose la question lundi et la pièce est tombée sur pile"
Nommons M l'évènement : "on lui pose la question mardi"


et

Donc finalement on a :






Les probabilités de R selon l'entretien sont :




Donc par la formule de la probabilité totale,

Je ne suis pas sur qu'il y ai paradoxe, d'après moi elle à toujours une chance sur 2 d'avoir raison.

Bonjour Lolo

Je suis assez d'accord avec toi et personnellement, je vois les choses de façon beaucoup plus simple !

On lance la pièce une fois... et cela n'a aucune conséquence sensible pour Aurore (puisque si on la rendort, on lui fait oublier qu'elle a été réveillée !... et qu'elle ignore totalement le jour où on est)

Donc finalement l'expérience se résume à quelque chose de très simple : on lance une pièce... et un moment après on demande à quelqu'un de faire un pronostic !

En disant "elle est tombée sur pile", Aurore a une chance sur deux d'avoir raison.

MM

Bonjour lo !

Je ne suis pas d'accord, car ici, il n'y a seulement que 2 événements à considérer :

-la piece est tombé sur face -> on lui pose la question lundi
-la piece est tombé sur pile -> on lui pose la question lundi et mardi

Or, ce qui est trompeur c'est qu'on ne peut pas appliquer les probabilité conditionnelle car ces deux
événements conduisent a 2 autres événements qui ne sont pas distinct.

Pour déterminer la probabilité d'être interroger lundi ou mardi, on fait un cycle pile-face.
On a alors lundi(F)-lundi(P)-mardi(P) d'où le 2/3 qui est la probabilité pour aurore que la pièce soit tombé sur pile.

Bien sûr dans l'absolu c'est 1/2 mais on l'interroge 2 fois.
sur le lien de wiki :

Oui, je comprend ce que tu as dit dans ton 1er message : ce sont bien 2 questions différentes.
Néanmoins si Aurore veut gagner de l'argent, je lui conseille de répondre pile à chaque fois car on l'interroge plus souvent lorsque c'est pile.
Elle aura donc raison plus souvent.

Perso je suis pro "2/3"
En effet sachant qu'un entretien à lieu il y'a plus de chance que la pièce soit tombée sur Pile.

Pour mieux se représenter la situation on peut imaginer cette fois qu'au lieu de la réveiller quand la pièce tombe sur face on la poignarde dans son sommeil.
Dans ce cas la si elle est réveillée pour un entretien c'est forcément que la pièceest tombé sur pile.

Daxtero :

La plupart des "paradoxes" en mathématiques viennent du fait qu'une ambiguïté de vocabulaire roule l'auditeur dans la farine (par exemple en logique : un cheval bon marché est cher !) ou (c'est souvent le cas en probabilité) que le problème est posé de façon ambigu et que la question n'a carrément pas de sens (voir par exemple l'éternel problème des trois portes, très bien traité par Jean-Paul Delahaye dans un article de Pour la Science).

Ici nous sommes dans le deuxième catégorie et la question n'a aucun sens car l'expérience est mal définie.

Je prends une analogie :
Je suis dans un pays où la météo n'a que 2 possibilités : Beau ou Moche.
Au premier janvier, il fait beau.
Ensuite, il fait beau avec un une probabilité de 0,8 si il faisait beau la veille, et de 0,4 s'il faisait moche la veille.

Je connais cette règle mais j'ai totalement oublié la météo des jours précédents et je suis enfermé à la cave...sans calendrier.

On me demande quel temps il fait et je réponds "il fait beau"... quelle est la probabilité que j'ai raison.

On sent ici que la question n'a aucun sens si on ne sait pas quel jour est posé la question !

et qui calcule cette probabilité ? moi ou une personne extérieure qui sait quel jour on est ?

la question prend du sens si on affine l'énoncé... par exemple on peut dire qu'on me pose chaque jour la question, pendant un an, et qu'on considère la variable aléatoire X qui comptabilise le nombre de fois où j'ai eu raison... c'est à dire le nombre de jours de beau temps. Alors on peut calculer l'espérance mathématique de X qui, divisé par 365, me donnera "en moyenne" la probabilité pour que je sois dans le vrai un jour donné.

Revenons au problème d'Aurore... ici le problème est encore plus "maquillé" puisque le nombre de questions n'est pas fixe. Mais en aucun cas il n'y aura 3 réponses...!

Si un observateur extérieur, connaissant le jour, se pose la question, la réponse est simple :
Si sa réponse est fournie le lundi, la probabilité qu'elle ait raison est 1/2
Si sa réponse est fournie le mardi, la probabilité qu'elle ait raison est 1.

Si c'est Aurore qui se pose la question... et décide de répondre "pile" sans jamais modifier sa réponse,
Pour elle, la suite de l'expérience n'a aucune influence puisqu'elle oublie à chaque fois qu'on lui a posé la question si Pile est sorti ! On peut très bien réitérer une infinité de fois la chose dans ce cas (chaque jour on lui demande et on la rendort ...). Cela ne change rien au problème et que répondraient les partisans du 2/3 ????
Donc son point de vue est des plus simples : on la réveille à un moment donné (tous sont équivalents et indépendants pour elle) et on lui dit qu'on a lancé une pièce... la probabilité que Pile soit sorti vaut tout simplement 1/2 !
Même si elle veut se compliquer la vie en se posant la question du jour où l'on est, elle va mener le raisonnement suivant :
Soit la pièce est tombée sur Pile et on est Lundi ou Mardi, chacun avec une probabilité de 1/2
Soit elle est tombée du face est on est lundi avec une probabilité de 1 et mardi avec une probabilité de 0. L'analyse de cet "arbre" lui donne à nouveau une probabilité de 1/2 que la pièce soit tombée sur Pile

D'un point de vue extérieur, sans connaître le jour (disons qu'on me pose la question le mercredi), on peut aussi considérer le nombre de fois où la question sera posée (2 possibilités : 1 ou 2 fois, chacun avec une probabilité 1/2 puisque cela dépend du résultat du lancer) et considérer X la variable aléatoire comptabilisant le nombre de fois où elle a eu raison.
X ne peut valoir que 0 ou 2... et P(X=0)=1/2 (c'est le cas où face est sorti) et P(X=2)=1/2 (cas où pile est sorti).
L'espérance de X vaut donc 1... ramené au nombre de possibilités équiprobables, on retrouve une moyenne de 1/2.

MM

Bonjour !
Je change la question :
Sachant qu'on lui remet 50 euros à chaque entretient si son hypothèse est correcte, que doit-elle répondre pour gagner le plus d'argent ?

La réponse est qu'elle doit dire face, car en moyenne on vas lui poser 2 fois la question lorsque c'est pile contre 1 fois quand c'est face.

Dans le cas ou on la poignarde dans son sommeil quand la pièce tombe sur face, si elle se réveille voila le raisonnement qu'elle peut formuler.

sachant que je suis révellée c'est que la pièce est tombée sur pile car si la pièce était tombée sur face je n'existerais plus donc je ne pourrais plus réfléchir à ce problème, or je suis en train d'y réfléchir. Donc la pièce est bien tombé sur pile.

Dans le problème de base le calcul des probabilité ce fait dans la même façon que dans "le cas limite" ( quand on la poignard )

ben non ! parce que si on la poignarde, elle ne peut pas répondre... donc elle a une probabilité nulle d'avoir raison !