Bonjour

Pourrais-tu nous montrer la figure ?

Oui bien sur
mais j'ai juste un problème pour l'insérer dans le forum

Choisis un format peu gourmand en mémoire (GIF par exemple ou PNG). Tu peux faire ton dessin avec Géogebra, ou sinequanon ou paint et l'enregistrer dans l'un de ces formats.

Ou bien : décris-nous le plus précisément possible la figure.

voici l'image
seule dimension connue : AC = 16 cm
merci par avance pour votre aide

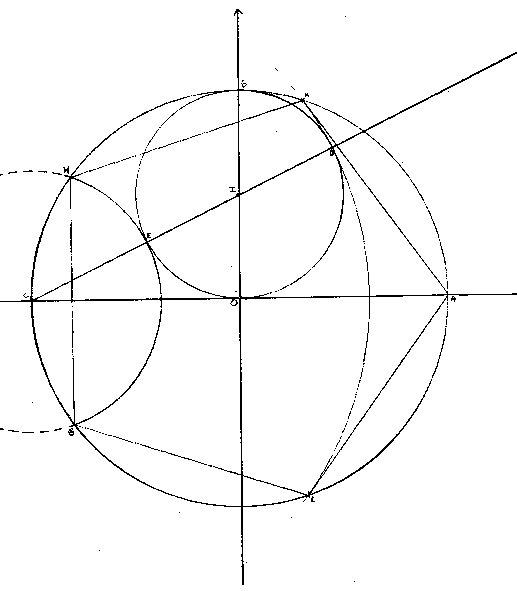
je dois démontrer que AKHGL est un pentagone régulier par la méthode de mon choix.

Avez vous une idée de la méthode à utiliser, une piste...
Dois-je utiliser la trigo, les complexes, les coordonnées polaires...
J'ai essayé plusieurs choses mais aucune ne m'amène au résultat.

Mon professeur dit que la figure est extraite d'un exercice de 4eme 3eme et qu'il a enlevé toutes les questions pour qu'on recherche une stratégie en mettant en oeuvre nos connaissances.
Merci

Ce n'est pas très évident directement. Connais-tu cos(2/5) ? Si oui, tu peux essayer de démontrer que c'est abscisse du point  K, multipliée par 8 car ton cercle a pour rayon 8.

Je suppose que I est le milieu de [OB].
Tu peux calculer CI puis CE puis HG ...

Je dois m'absenter pendant une heure ou deux. Peut-être qu'lqu'un d'autre pourra t'aider entre temps...

j'ai déjà calculé CI et CE. Comment ffaire pour HG ??
Je ne peux pas faire cos (2 pi / 5) car c'est ce qu'on cherche.
Je veux démontrer que les 5 angles au centre sont égaus à cet mesure

quelqu'un peut-il m'aider???

Je suis bloquée... je ne sais plus quoi faire

J'ai essayé toutes les méthodes que je connaissais

Je reviens pour essayer de te donner quelques pistes.

Pour ce genre de problème, il faut commencer par calculer cos(2/5).

Si AKHGL est un pentagone régulier, alors

On peut en déduire que 8(cos(0)+cos(2/5)+cos(4/5)+cos(6/5)+cos(8/5))=0.

Par ailleurs, on peut facilement voir que cos(2/5)=cos(8/5) et que cos(4/5)=cos(6/5)De plus en utilisant la formule cos(2a)=2cos²a, on peut tout écrire en utilisant seulement cos(2/5).

On montre ainsi que cos(2/5) est solution de l'équation 4x²+2x-1=0.

Si tu parviens alors à démontrer que l'abscisse du point K est égale à 8cos(2/5), c'est gagné...

J'ai refais la figure pour mieux voir les points.

J'ai fait une erreur. La formule est cos(2a)=2cos²a-1 et non pas 2cos²a ...

Comment je trouve les coordonées du point K ?

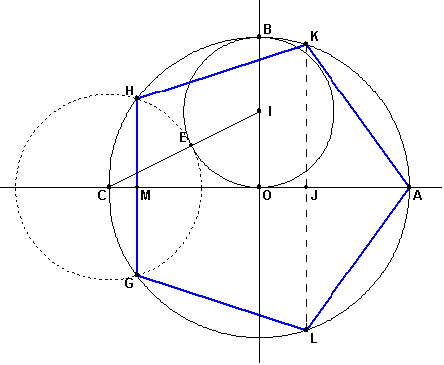
J'ai réussi à démontrer que l'angle AOK valait 2pi/5
Comme AO = 8 je trouve les coordonnées cartésiennes de K
xK = 8 cos (2pi/5)
yk = 8 sin (2pi/5)

Que dois-je faire après?

A quoi correspond l'équation 4x2+2x-1=0 s'il vous plait ?

Bonjour

Pierre (si j'ai bien compris) se sert de 4x²+2x-1=0
pour calculer la valeur exacte de cos(2pi/5)
puisque cos(2pi/5) est la racine positive de cette équation.

Peux-tu m'expliquer comment tu as montré (juste le plan pas les détails) que:  
AOK valait 2pi/5 SANS utiliser que

À quoi correspond l'équation 4x²+2x-1=0 ?

On suppose que AKHGL est un pentagone régulier et, de ce fait, l'angle AOK vaut 2/5.
Posons OJ=8cos(2/5)=8x
On sait que OM=8cos(4/5)=8(2cos²(2/5)-1).
Donc OM=8(2x²-1)=16x².-8

D'après ce que j'ai dit hier soir (20:25), on a :

Donc, en utilisant les projections sur l'axe horizontal : OA+OJ-OM-OM+OJ=0

ou encore : 8+2OJ-2OM=0

ou encore : 8+2(8x)+2(16x²-8)=0

ou encore 32x²+16x=0

finalement : 8(4x²+2x-1)=0.

On résout cette équation ce qui permet de trouver la valeur de cos(2/5)

Ensuite, on peut calculer CE=CH. On trouve CE=

Ensuite, en utilisant les relations dans les triangles rectangles, on peut trouver OM=.

Je te laisse faire la suite...